[OS] 교착상태(DeadLock)

mingsso·2023년 11월 1일

CS

목록 보기

24/30

1️⃣ 교착상태 개념

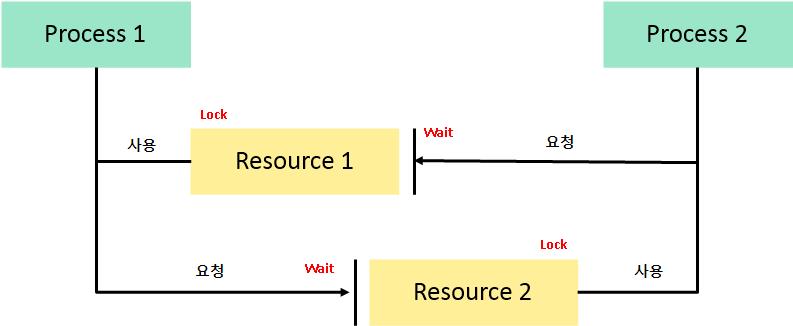
둘 이상의 프로세스가 다른 프로세스가 점유하고 있는 자원을 서로 기다릴 때 무한 대기에 빠지는 상황

식사하는 철학자 문제

-> 교착상태를 설명하기 위한 문제로, 다익스트라가 만듦

5명의 철학자가 원탁에 앉아서 식사를 함. 이때 철학자들 사이에는 포크가 하나씩 놓여 있고 철학자들은 다음의 과정을 통해 식사를 함

일정 시간 동안 생각한다
왼쪽 포크가 사용 가능해질 때까지 대기한다. 포크가 사용 가능해지면 포크를 집어든다
오른쪽 포크가 사용 가능해질 때까지 대기한다. 포크가 사용 가능해지면 포크를 집어든다
양쪽의 포크를 잡으면 일정 시간 동안 식사한다
오른쪽 포크를 내려놓는다
왼쪽 포크를 내려놓는다
다시 1번으로 돌아간다

5명의 철학자 전부 왼쪽 포크를 들고 있다면, 오른쪽 포크를 얻으려고 할때 오른쪽 포크는 이미 상대방이 가져간 상태이므로 모든 철학자들이 3번 상태에 머무르며 자기 오른쪽 포크가 사용 가능해질 때까지 영원히 기다리고만 있는 교착상태에 빠지게 됨

2️⃣ 교착상태 발생 조건

4가지 모두 성립해야 발생함! 하나라도 성립하지 않으면 교착상태 문제 해결 가능

상호배제 - 한 번에 한 프로세스만 해당 자원을 사용할 수 있음
점유와 대기 - 한 프로세스가 자원을 점유하고 있으면서 또 다른 자원을 요청하여 대기하고 있는 상태여야 함
비선점 - 다른 프로세스에 할당된 자원은 사용이 끝날 때까지 강제로 빼앗을 수 없음
순환 대기 - 대기 프로세스 집합이 순환 형태로 자원을 대기하고 있어야 함

3️⃣ 교착상태의 해결방법

1. 예방

👉🏻 데드락의 발생조건 4가지 중 하나라도 발생하지 않게 함

상호배제 금지 - 한 번에 여러 프로세스가 동시에 자원을 공유해서 사용할 수 있도록 함
점유와 대기 금지 - 프로세스 실행에 필요한 모든 자원을 한꺼번에 요구하고 허용할 때까지 작업을 보류해서, 나중에 또다른 자원을 점유하기 위한 대기 조건을 성립하지 않도록 함
비선점 금지 - 우선순위가 높은 프로세스가 해당 자원을 선점할 수 있도록 함
순환 대기 금지 - 자원을 순환 형태로 대기하지 않도록 일정한 한 쪽 방향으로만 자원을 요구할 수 있도록 함

But, 시스템의 처리량이나 효율성을 떨어트리는 단점

2. 회피

안정 상태 - 시스템의 프로세스들이 요청하는 모든 자원을, 데드락을 발생시키지 않으면서도 차례로 모두에게 할당해 줄 수 있는 상태
안정 순서 - 안정 상태를 만들 수 있는 순서
불안정 상태 - 안정 상태가 아닌 상태. 즉, 데드락 발생 가능성이 있는 상태이며, 교착 상태(데드락)는 불안정 상태일 때 발생할 수 있음 → 교착 상태가 불안정 상태의 부분집합

👉🏻 안정 상태가 유지될 수 있을 때만 시스템에 자원을 할당함 → 은행원 알고리즘

2-1. 은행원 알고리즘

다익스트라가 제안한 기법으로, 어떤 자원의 할당을 허용할지를 결정하기 위해 각 프로세스의 최대 자원 요청량을 가지고 시뮬레이션 해서, 안정 상태가 유지될 수 있을 때만 자원을 할당함

예시1)

처음에 시스템이 총 12개의 자원을 가지고 있다고 가정할 때,

P0~P2는 프로세스이고, Max는 각 프로세스마다 최대 자원 요청량, Allocation은 현재 프로세스에 할당 중인 자원의 양, Need는 남은 필요한 자원의 양

현재 t0일 때 프로세스에 할당된 자원의 합은 5+2+2 = 9개, 현재 Available 자원은 12-9 = 3개

→ 순서가 <P1, P0, P2> 일 때 안전 순서를 만족함

P1은 2개가 이미 할당되어 있고, 2개를 추가적으로 할당받기를 기다리고 있음 → 현재 Available 자원은 3개이므로, 이 중에 2개를 P1에게 할당해줌 (현재 Available은 3-2 = 1개)
실행이 끝난 P1은 자신에게 할당되어 있던 자원 4개를 모두 반납함 (현재 Available은 1+4 = 5개)
현재 Available 자원이 5개이고, 이를 P0에게 모두 할당해 주면 P0도 실행 가능해짐 (현재 Available은 5-5 = 0개)
실행이 끝난 P0은 자신에게 할당되어 있던 자원 10개를 모두 반납함 (현재 Available은 0+10 = 10개)
마지막으로 P2에게 자원 7개를 할당해줌 (현재 Available은 10-7 = 3개)
실행이 끝난 P2는 자신에게 할당되어 있던 자원 9개를 모두 반납함 (현재 Available은 3+9 = 12개)

예시2)

만약 예시1에서 P2가 처음에 자원을 하나 더 할당받고 있었다면?

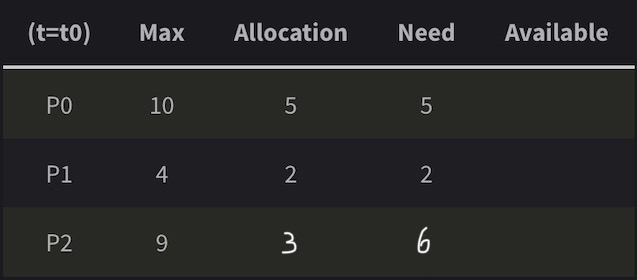
현재 t0일 때 프로세스에 할당된 자원의 합은 5+2+3 = 10개, 현재 Available 자원은 12-10 = 2개

P1은 2개가 이미 할당되어 있고, 2개를 추가적으로 할당받기를 기다리고 있음 → 현재 Available 자원은 2개이므로, 이 중에 2개를 P1에게 할당해줌 (현재 Available은 2-2 = 0개)
실행이 끝난 P1은 자신에게 할당되어 있던 자원 4개를 모두 반납함 (현재 Available은 0+4 = 4개)

→ 4개의 자원으로는 P0나 P2를 해결해 줄 수 없음 (데드락 발생)

But. 은행원 알고리즘의 경우, 항상 불안전 상태를 방지해야 하므로 자원 이용도가 낮고, 각 프로세스의 최대 자원 요청량을 미리 알아야 하는 등 사용에 있어 제약 조건이 많음

3. 탐지 및 복구

3-1. 탐지

Allocation, Request, Available 등으로 시스템에 데드락이 발생했는지 여부를 탐색함. 즉, 은행원 알고리즘에서 했던 방식과 유사하게 현재 시스템의 자원 할당 상태를 가지고 파악함
이 외에도 자원 할당 그래프를 통해 탐지하는 방법도 있음

3-1-1. 자원 할당 그래프

방향 그래프로, 정점 V의 집합과 방향 간선 E의 집합으로 구성됨

프로세스의 집합 P = {P1, P2, ... , Pn} → 원으로 표시함
자원 유형의 집합 R = {R1, R2, ... , Rn} → 사각형으로 표시함
요청 간선 Pi → Rj : 프로세스 Pi가 자원 Rj의 인스턴스 하나를 요청하고 있는 상태 (현재 프로세스가 해당 자원을 기다림)
할당 간선 Rj → Pi : 자원 Rj의 한 인스턴스가 프로세스 Pi에 할당된 상태

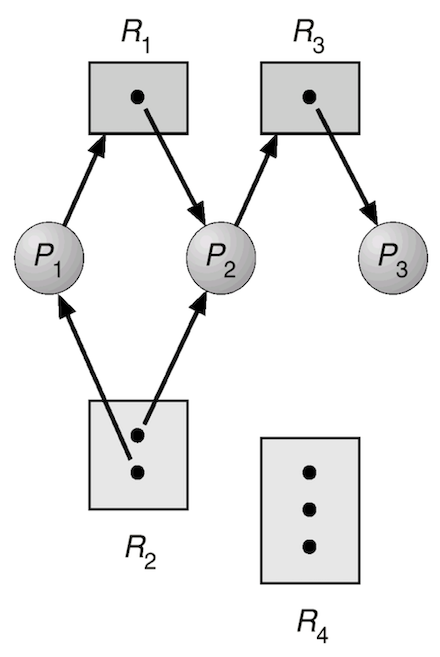
자원 할당 그래프에서 사이클이 없다면 교착상태는 발생하지 않음!

만약 사이클이 존재할 경우

각 자원 집합마다 하나씩의 자원밖에 없다면 교착상태는 반드시 발생함

각 자원 집합마다 여러 개의 자원이 있다면 교착상태가 발생할 가능성이 있음

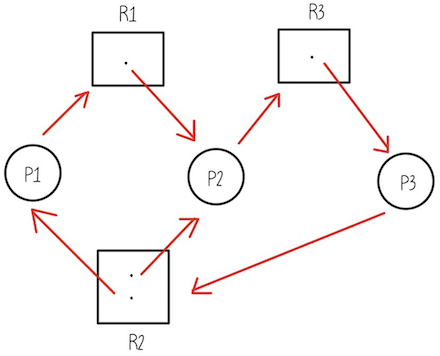
사이클이 2개(하트, 오른쪽)가 만들어졌으므로, 자원 2개가 있음에도 불구하고 진행이 불가능한 상황이 됨 → Deadlock 발생

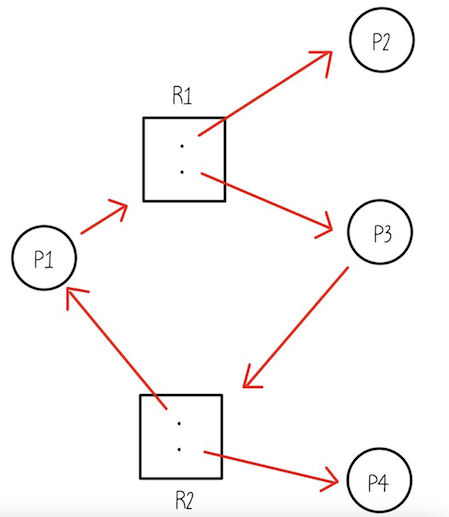
사이클이 있음에도 불구하고, P2와 P4가 자원을 반납하면 데드락 문제가 해결됨 → Deadlock이 아님

3-2. 복구

교착 상태를 일으킨 프로세스를 종료하거나, 할당된 자원을 해제시켜 복구함

프로세스를 1개 이상 중단시키기
- 교착 상태에 빠진 모든 프로세스를 중단시키는 방법 : 계속 연산중이던 프로세스들도 모두 일시에 중단되어 부분 결과가 폐기될 수 있는 부작용이 발생할 수 있음
- 프로세스를 하나씩 중단 시킬 때마다 탐지 알고리즘으로 데드락을 탐지하면서 회복시키는 방법 : 매번 탐지 알고리즘을 호출 및 수행해야 하므로 부담이 되는 작업일 수 있음
자원 선점하기
- 교착 상태의 프로세스가 점유하고 있는 자원을 선점해 다른 프로세스에게 할당함 (해당 프로세스는 일시정지) → 우선순위가 낮은 프로세스 위주로 프로세스 자원 선점