1️⃣ 개념
플로이드-워셜 알고리즘
모든 정점 쌍 사이의 최단 거리를 구하는 알고리즘
음수인 간선이 있는 건 상관없고 음수인 사이클이 있을 때만 문제가 발생함
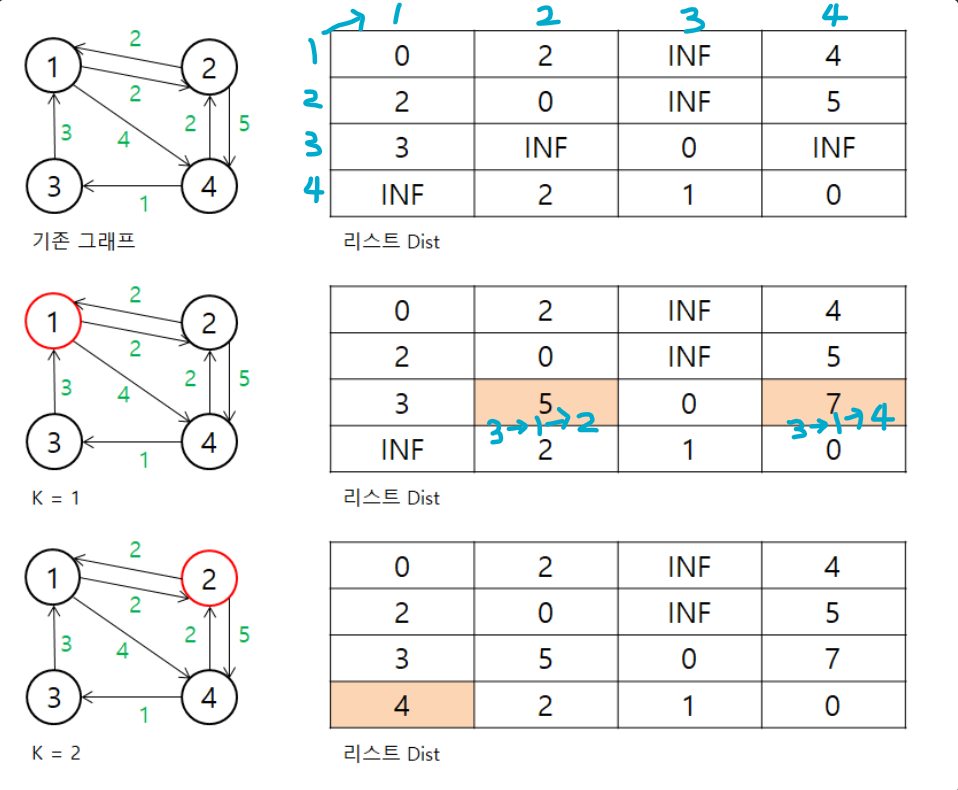
- 하나의 정점에서 다른 정점으로 바로 갈 수 있으면 최소 비용을, 갈 수 없다면 INF로 배열에 값을 저장함
- 3중 for문을 통해 거쳐가는 정점을 설정한 후, 해당 정점을 거쳐가서 비용이 줄어드는 경우에는 값을 바꿔줌
- 위의 과정을 반복해 모든 정점 사이의 최단 경로를 탐색함
def Floyd():
dist = [[float('inf')] * n for _ in range(n)] # 최단경로를 담는 배열
for i in range(n):
for j in range(n):
dist[i][j] = a[i][j]
for k in range(n): # 거치는 점
for i in range(n): # 시작점
for j in range(n): # 끝점
# k를 거쳤을 때 경로가 더 적은 경로
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist다익스트라 알고리즘
하나의 시작점으로부터 다른 모든 정점까지의 최단거리를 구하는 알고리즘
음수의 가중치를 가지는 간선이 있으면 아예 사용할 수 없음, 사이클도 없어야 함
💡 다익스트라가 발견한 초기 방법 - O(V^2+E)
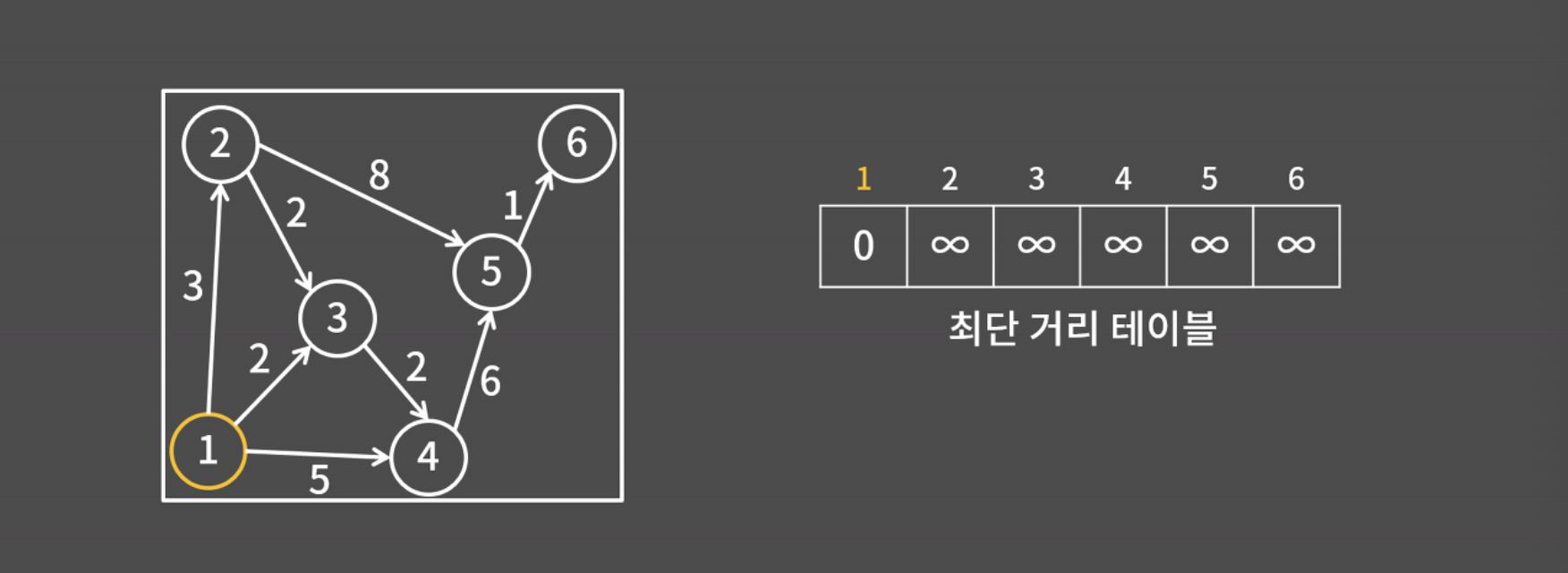
- 1번 정점을 시작점이라고 할 때, 현재 1번 정점에서는 2,3,4번 정점으로만 갈 수 있는데, 각 정점까지의 최단거리는 각각 3,2,5임
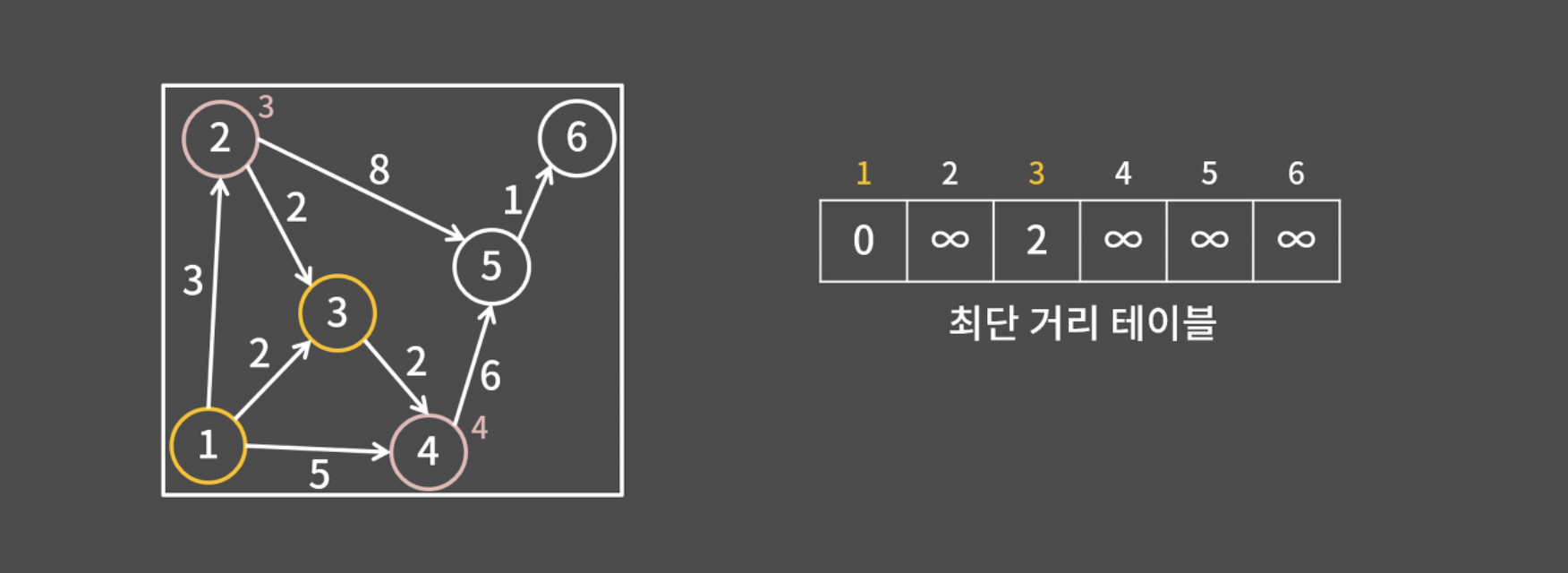
- 가장 가까운 건 3번 정점이기 때문에 3번 정점까지의 거리를 2로 확정함
- 거리가 확정된 1,3번 정점에서 갈 수 있는 정점은 2,4번 정점인데, 2번 정점까지의 거리는 3이고, 4번 정점까지의 거리는 4가 됨
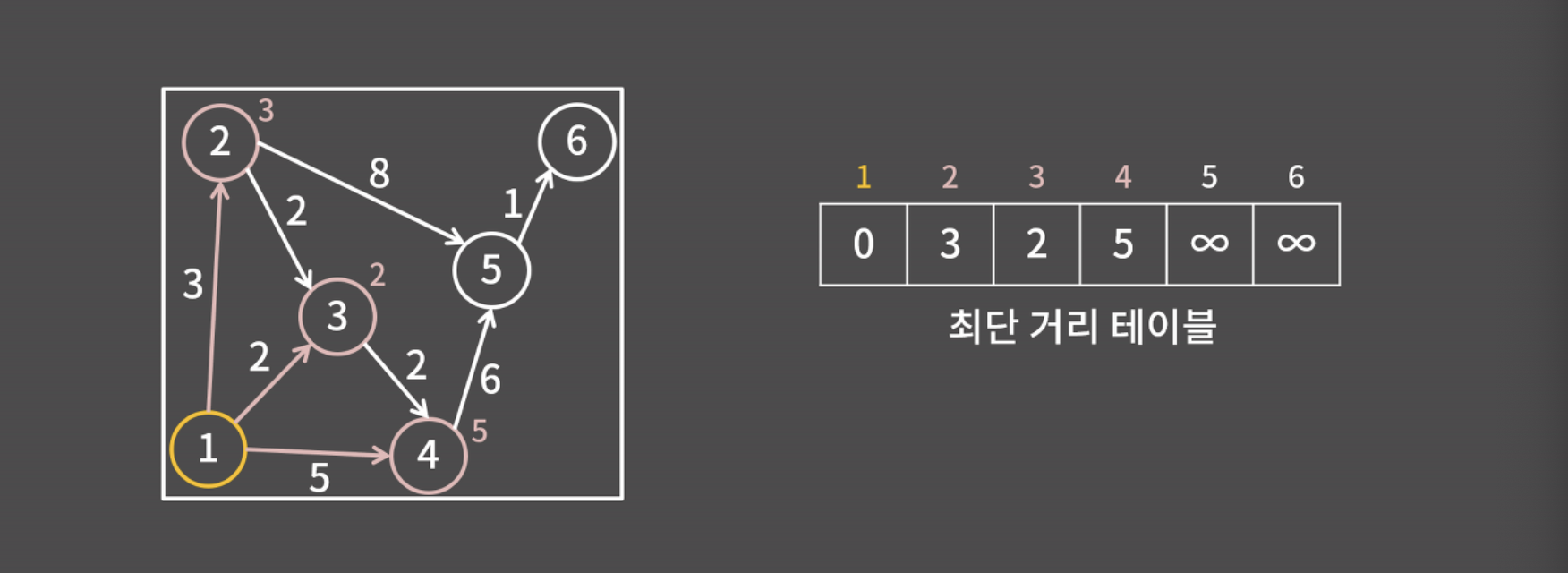
1-1. 거리를 계산할 때 일단 최단 거리 테이블에 3,2,5를 써놓고, d[2]부터 d[6] 중에서 최소값을 찾으면 값을 정할 수 있음(3번 정점 2)
3-1. 1번 정점에서 뻗어나가는 간선은 이미 다 확인했기 대문에, 3번 정점에서 뻗어나가는 간선만 봄
-> 3번 정점에서 4번 정점으로 가는 간선이 있는데 이 간선을 이용하면 d[4] = d[3] + 2 = 4
- 이 4는 원래 테이블에 적혀있던 d[4]=5보다 작기 때문에 d[4]를 4로 바꿈
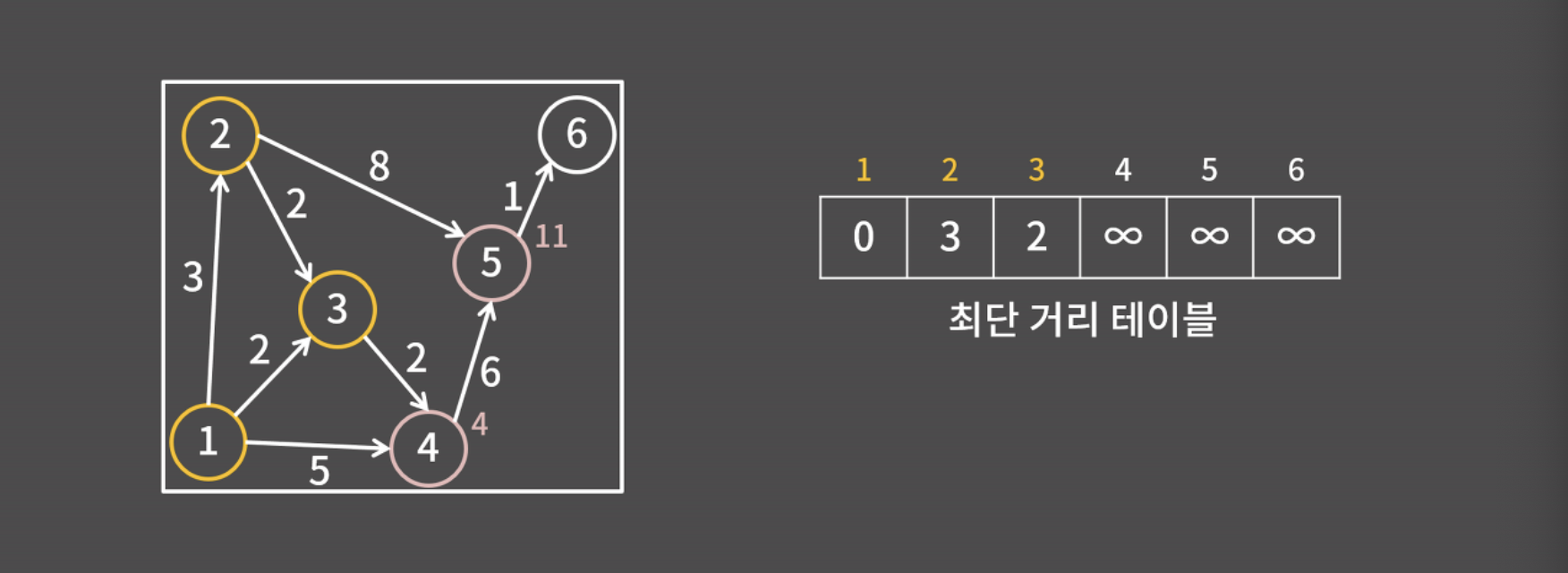
- 둘 중 더 가까운 건 2번 정점이기 때문에 2번 정점까지의 거리를 3으로 확정함
- 1,2,3번 정점에서 갈 수 있는 정점은 4,5번 정점인데, 4번 정점까지의 거리는 4이고, 5번 정점까지의 거리는 11임
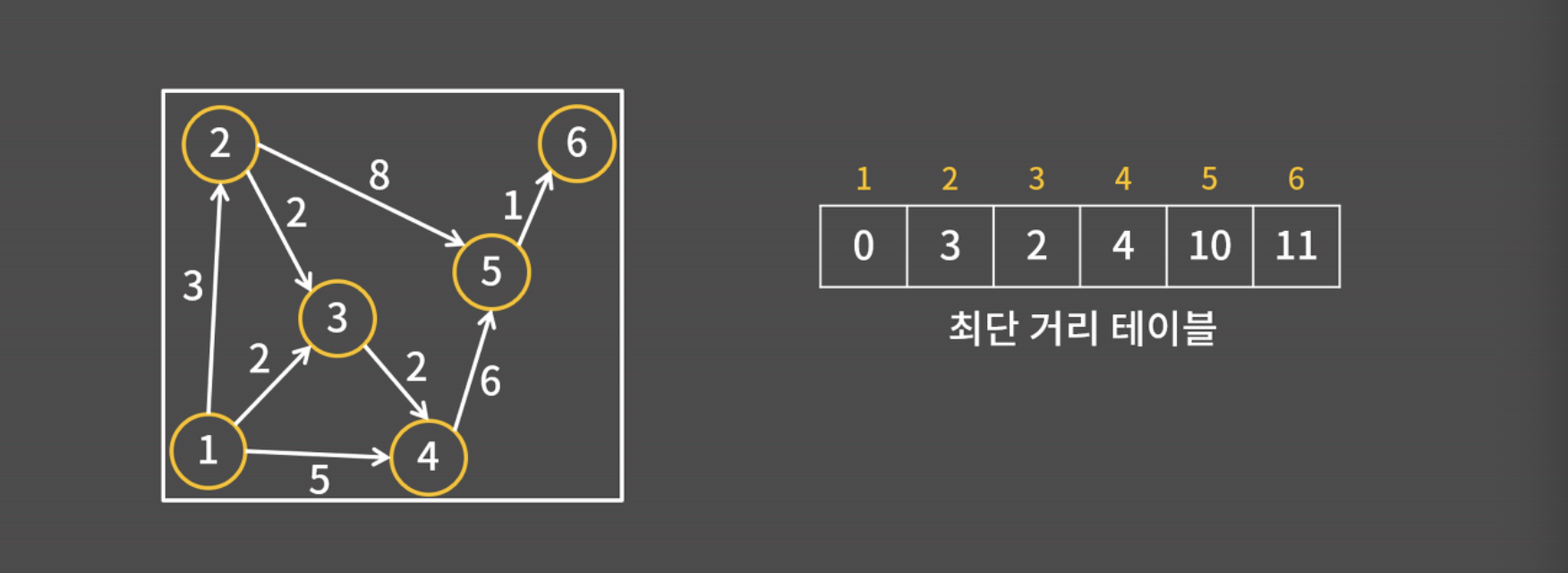
- 둘 중 더 가까운 건 4번 정점이기 때문에, 4번 정점까지의 거리를 4로 확정함
- 1,2,3,4번 정점에서 갈 수 있는 정점은 5번 정점밖에 없고, 5번 정점까지의 거리는 10임
- 마지막으로 1,2,3,4,5번 정점에서 갈 수 있는 정점은 6번 정점밖에 없고, 6번 정점까지의 거리는 11임
❓ 다익스트라 알고리즘이 음수 간선을 처리할 수 없는 이유
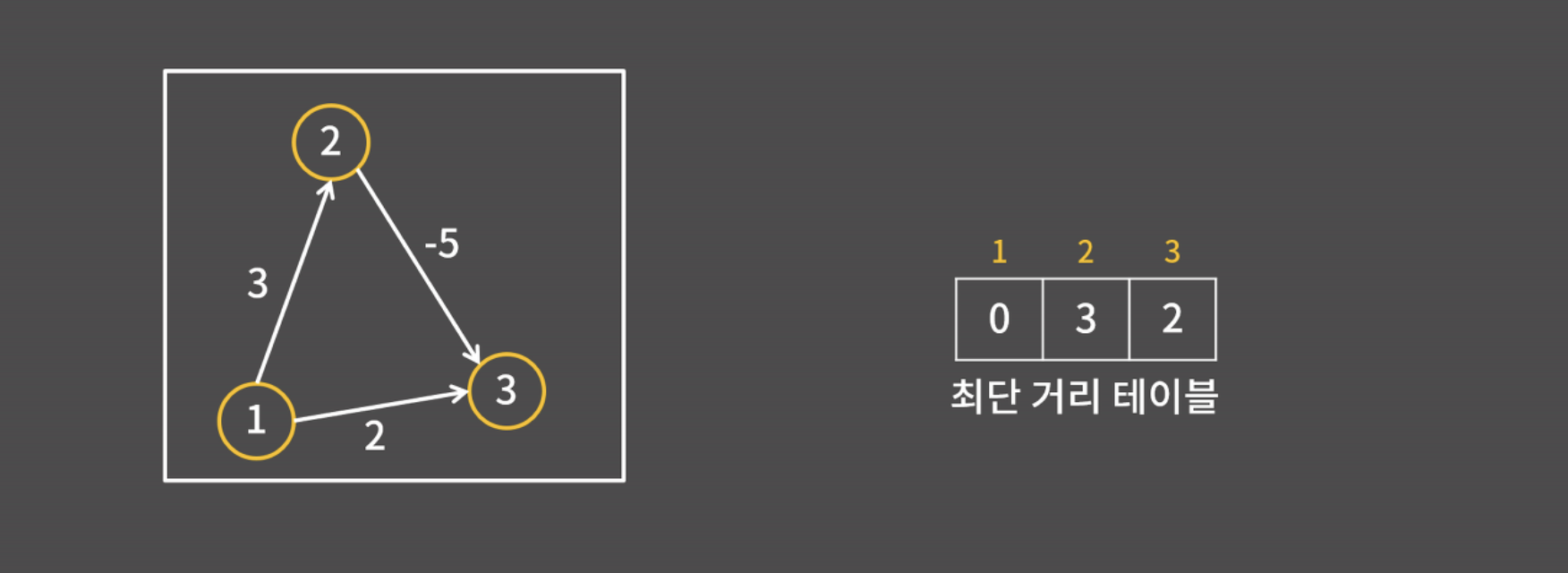
3번 정점까지의 최단 거리는 2가 아니라 1->2->3번 경로로 얻을 수 있는 -2가 됨
즉, 음수 간선이 있으면 현재 갈 수 있는 정점 중에서 가장 가까운 정점까지의 거리를 확정할 수 없어서 다익스트라 알고리즘의 논리가 성립 불가함
⭐️ 우선순위 큐를 이용하는 개선된 방법 - O(ElgE)
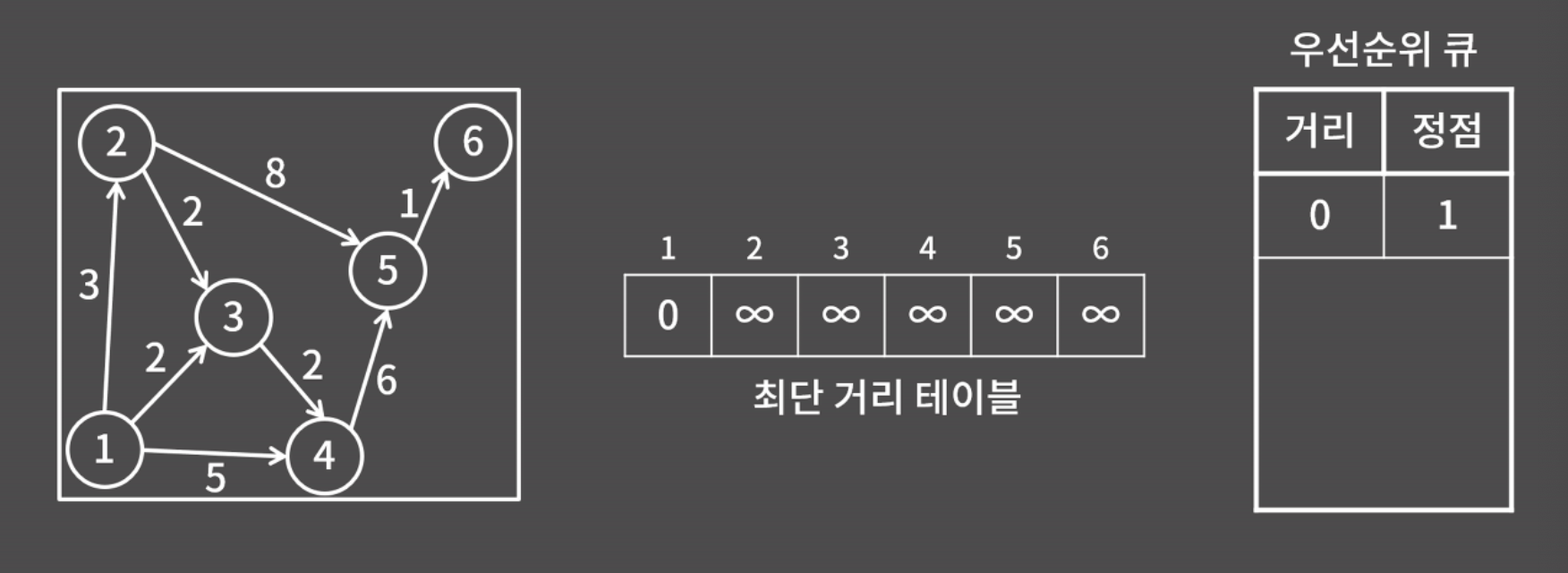
- 최단 거리 테이블을 0과 ∞로 채워두고, (0, 시작점)을 우선순위 큐에 넣음
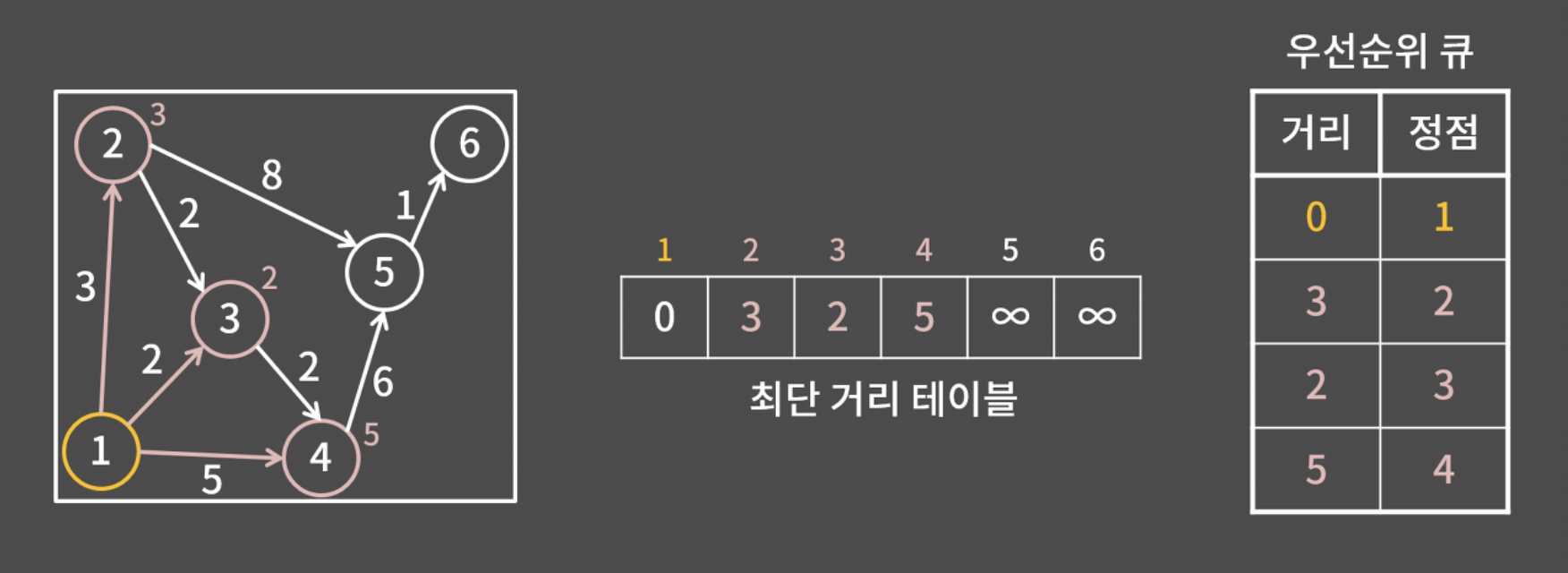
- 우선순위 큐에서 가장 거리가 작은 원소인 (0, 1)을 선택하고 제거함
- 1번 정점에서 갈 수 있는 정점은 2,3,4번 정점이고, 거리는 3,2,5인데 원래 최단 거리 테이블에 있던 ∞보다 작으니까 최단 거리 테이블을 셋 다 갱신해줌
- 힙에 (3,2), (2,3), (5,4)를 추가함

- 우선순위 큐가 비어있지 않기 때문에 우선순위 큐에서 가장 거리가 작은 (2,3)을 선택하고, d[3]=2인지 확인함
- 3번 정점(d)에서 갈 수 있는 정점은 4번 정점(i)이 있고, 3번 정점을 거쳐서 4번 정점으로 갈 때의 최단 거리는 d[3]+2=4임 -> 우선순위 큐에 (4,4)를 삽입함

- 우선순위 큐가 비어있지 않기 때문에 우선순위 큐에서 가장 거리가 작은 (3,2)를 선택하고, d[2]=3인지 확인함
- 2번 정점에서 갈 수 있는 정점은 3,5번 정점이 있고, 2번 정점을 거쳐서 각각으로 가는 거리는 5,11임 -> 2<5이기 때문에 3번 정점은 갱신되지 않고 5번 정점만 갱신되며, 우선순위 큐에 (11, 5)를 삽입함

- 우선순위 큐가 비어있지 않기 때문에, 우선순위 큐에서 가장 작은 (4,4)를 선택하고, d[4]=4인지 확인함
- 4번 정점에서 갈 수 있는 정점은 5번 정점이 있고, 4번 정점을 거쳐서 5번 정점으로 가는 거리는 10임 -> 10<11이기 때문에 갱신되며, 우선순위 큐에 (10, 5)를 삽입함
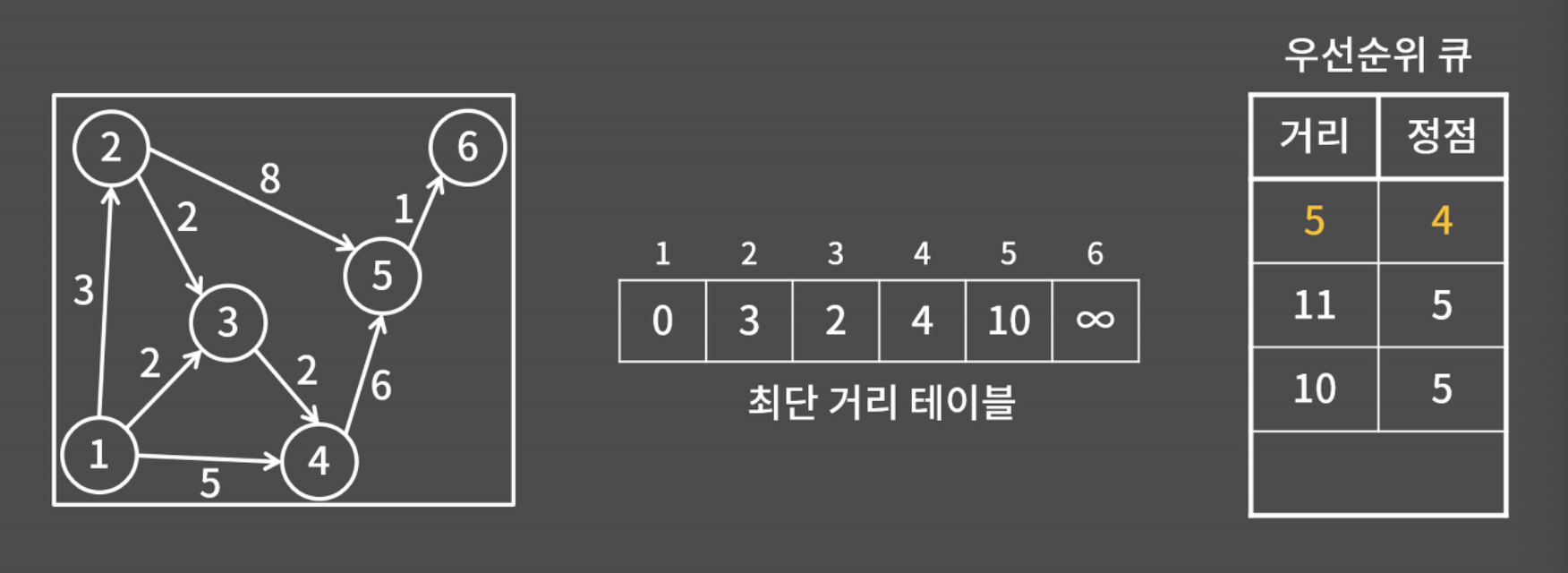
- 우선순위 큐에서 가장 작은 (5,4)가 선택되지만, d[4]가 5가 아니기 때문에 아무 처리도 하지 않고 건너뜀
- 다음으로 (10,5)가 선택될 것이고, d[5]=10이기 때문에 과정을 이어감
- 이런 식으로 우선순위 큐가 빌 때까지 반복함
1. 1차원 다익스트라
# graph = [[연결된 간선, 간선의 가중치]]
import heapq
dist = [float('inf') for _ in range(n)]
def dijkstra(start):
minHeap = []
heapq.heappush(minHeap, [0, start]) # 시작 노드
dist[start] = 0
while minHeap:
# 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
d, now = heapq.heappop(minHeap)
# 최단거리 테이블과 일치하는지 확인
if dist[now] != d:
continue
# 선택된 노드와 인접한 노드를 확인
for i in graph[now]:
cost = d + i[1] # 거리와 간선의 가중치 합침
# 선택된 노드를 거쳐서 이동하는 것이 더 빠른 경우
if cost < dist[i[0]]:
dist[i[0]] = cost # 최단거리 테이블 갱신
heapq.heappush(minHeap, [cost, i[0]])
2. 2차원 다익스트라
def dijkstra():
minHeap = []
heapq.heappush(minHeap, [cave[0][0], 0, 0])
dist[0][0] = cave[0][0]
while minHeap:
d, y, x = heapq.heappop(minHeap)
if y == (n - 1) and x == (n - 1):
break
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n:
cost = d + cave[ny][nx]
if cost < dist[ny][nx]:
dist[ny][nx] = cost
heapq.heappush(minHeap, [cost, ny, nx])크루스칼 알고리즘
가장 적은 비용으로 모든 노드를 연결하기 위해 사용
-> 최소 비용 신장 트리 생성
- 간선 데이터를 비용에 따라 오름차순으로 정렬함
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인함
-> 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킴 - 모든 간선에 대해 2번 과정을 반복함
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
v, e = map(int, input().split()) # 노드의 개수, 간선의 개수
parent = [0] * (v + 1) # 부모 테이블 초기화
edges = [] # 간선 정보
result = 0
# 부모 테이블 상에서 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# 모든 간선에 대한 정보를 입력 받기
for _ in range(e):
a, b, cost = map(int, input().split())
edges.append([cost, a, b])
edges.sort()
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
print(result)2️⃣ 문제 풀이
* 백준 최소비용 구하기 2 (🥇3)
https://www.acmicpc.net/problem/11779
n개의 도시와 한 도시에서 출발하여 다른 도시에 도착하는 m개의 버스가 있을 때, A번째 도시에서 B번째 도시까지 가는데 드는 버스 비용을 최소화 시키려고 한다.
A번째 도시에서 B번째 도시까지 가는데 드는 최소비용과 경로를 출력해라
dist = [INF] * (n + 1)
prev = [0] * (n + 1) # 이전 노드 저장
def dijkstra(start):
dist[start] = 0
minHeap = []
heapq.heappush(minHeap, [0, start])
while minHeap:
d, now = heapq.heappop(minHeap)
if dist[now] != d:
continue
for i in graph[now]:
cost = d + i[1]
if cost < dist[i[0]]:
dist[i[0]] = cost
prev[i[0]] = now
heapq.heappush(minHeap, [cost, i[0]])
dijkstra(s)
# end에서 이전 노드를 계속 거슬러가면 start가 나옴
path = [e]
now = e
while now != s:
now = prev[now]
path.append(now)
path.reverse()* 프로그래머스 섬 연결하기 (Level 3)
https://school.programmers.co.kr/learn/courses/30/lessons/42861
n개의 섬 사이에 다리를 건설하는 비용이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용
-> 크루스칼 알고리즘
* 프로그래머스 순위 (Level 3)
https://school.programmers.co.kr/learn/courses/30/lessons/49191
선수의 수와 경기 결과를 담은 배열이 매개변수로 주어질 때, 정확하게 순위를 매길 수 있는 선수의 수?
def solution(n, results):
answer = 0
board = [[0] * n for _ in range(n)]
for a, b in results:
board[a-1][b-1] = 1
board[b-1][a-1] = -1
for k in range(n):
for i in range(n):
for j in range(n):
if i == j or board[i][j] in [1, -1]:
continue
if board[i][k] == board[k][j] == 1:
board[i][j] = 1
board[j][i] = board[k][i] = board[j][k] = -1
for row in board:
# 자기자신만 0 -> 자기자신 제외 모든 나머지 선수들과 경기 결과가 있음
if row.count(0) == 1:
answer += 1
return answer 