알고리즘 언어로 JS를 사용하게 되면 발생하는 일

프론트엔드 개발자를 희망하며 힘들었던 순간 중 하나는 바로 알고리즘 테스트를 볼 때이다.

보통 코테 준비를 할 때 프론트 개발자는 python 혹은 JS를 사용하시는 분들로 나뉘어지는데,

나는 성격 자체가 하나에 몰빵하는 기질이 있어서 JS 외길인생을 선택했었다.

그러나 JS를 선택함에 있어서 정말 최악의 순간은 바로 알고리즘을 위한 라이브러리가 정말 불친절하다는 점이다.

실제로 JS는 아래의 자료구조가 단 한 개도 구현되어 있지 않다.

• 큐
• 스택
• 우선순위 큐
• 조합/순열
• 그 외…

물론 스택/큐는 간단히 배열을 두고 인덱스를 조작하여 복잡도를 최적화 할 수 있고,

조합/순열의 경우 그 원리만 파악하면 재귀를 사용하여 매우 간단히 구현이 가능해서 별 문제가 없다.

그러나 우선순위 큐의 경우 정말 밑바닥부터 직접 구현해야 한다.

실제로 정말 비참했던 순간이, 2024 CJ 올리브영 공채 코테였다

3문제가 출제 됐었고 실제 난이도는 3>2>1 순이었다.

• 3번은 올리브영에서 의도하고 킬러문항으로 내놓은 것 같았다.

• 2번은 시간 복잡도만 간단히 최적화하면 됐었다.

• 1번 문제는 뇌를 빼놓고도 풀 수 있는 쉬운 문제였다.

그러나 JS를 사용한다면 1번 문제에서 뇌를 다시 집어넣고 풀가동 해도 풀기 힘들다.

왜냐하면, 1번 문제가 무조건 우선순위 큐를 사용해야 하는 문제이기 때문이다.
JS를 사용한다면 이걸 직접 구현해야 했었으므로 난이도가 3>2>1에서 1>3>2로 뒤바뀌게 된다.

“아니 이러면 JS로 푸는 사람은 형평성에 어긋난거 아닌가?”

“???: 우린 JS로 풀라고 강제한적 없는데?ㅋ”

실제로 그 당시 올리브영 코테에서는 JS만 한정한게 아니라, 다른 언어도 모두 사용 가능했었다.

그러므로 알고리즘 언어로 JS를 사용하는 프론트 개발자는

JS로 직접 우선순위 큐를 구현하던가, 그게 자신없다면 1번 문제만이라도 python을 쓰던가 해야 했다.

나의 경우, 2 3번은 곧바로 풀었는데 1번에서 우선순위 큐 말고 다른 방법을 찾느라 1시간을 넘게 썼던 것 같다. 결국 못 품

너무 허탈했다. 그냥 python써서 import heapq 만 딸각하면 됐던 것을 왜 그렇게 하지 않았을까,,,

---

우선순위 큐를 안 쓰는 방법은 없을까?

위와 같은 올리브영 사례를 겪고 나서, 나름 우선순위 큐를 대체할 방법을 찾아보고 싶었다.

결론부터 말하자면, 완전히는 아니지만 일부 상황에서는 대체가 가능하다.

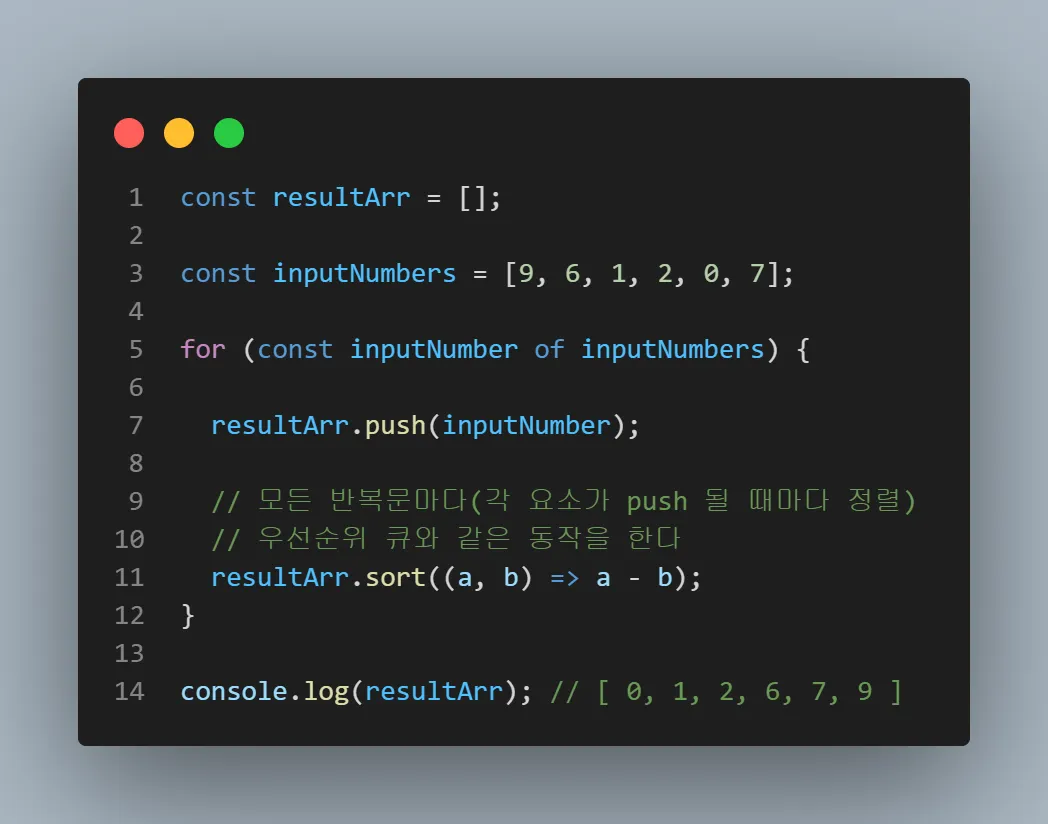
보통 JS에서 우선순위 큐를 사용해야 하는 문제를 풀 때, 임시 방편으로 .sort()메소드를 사용하는 경우는 다음과 같다.

• 각 반복문마다 특정 값을 배열에 push한다

• push와 동시에 특정 기준으로 정렬된 상태를 보장하고, 이렇게 정렬된 배열 상태를 기반으로
  추가적인 로직을 진행하기 위해 .sort() 를 사용한다.

원래는 정렬을 위해 우선순위 큐를 사용해야 하는게 맞지만, 동일한 동작을 보장하기 위해 임시방편으로 간편한 .sort()를 사용한 것이다.

위 로직은 직관적이긴 하지만, 당연히 웬만한 문제에서는 메모리 초과 or 시간 초과가 발생한다.

그렇다면 각각의 상황에서 어떻게 대처해야 하는지 알아보자.

시간 초과가 걸리는 경우 - 우선순위 큐를 사용할 수 밖에 없다

보석 도둑 문제가 대표적인 예시이다.

이처럼 .sort() 만 사용했을 때 시간초과가 발생하는 경우는 어쩔 수 없이 우선순위 큐를 사용해야만 한다.

• 만약 우선 순위 큐 없이 .sort() 메소드를 사용하면 O(NlogN) 가 발생하므로
  총 시간복잡도는 O( N * NlogN ) 이 된다.

• 반면, 우선순위 큐의 경우 삽입시 O(logN) 으로 정렬된 상태가 되므로
  총 시간 복잡도는 O( N * logN ) 이 된다.

이정도 시간 차이를 극복하려면 어쩔 수 없이 우선순위 큐를 쓸 수 밖에 없다

메모리 초과가 걸리는 경우 - 다른 알고리즘으로 간편히 대체가 가능하다❗❗

가운데를 말해요, 카드 정렬하기, 강의실 문제가 대표적인 예시이다

위의 문제들에서 우선순위 큐 없이 .sort() 만 사용하게 된다면 메모리 초과가 발생하게 된다.

그러나 이렇게 메모리 초과가 발생하는 경우에는 굳이 우선순위 큐까지 구현할 필요가 없다.
즉, 다른 간편한 알고리즘으로 대체가 가능하다

이 말은, 어떻게 보면 .sort() 메소드 자체가 기본적으로 메모리를 굉장히 많이 잡아먹는다는 것이다.

그렇다면 왜 .sort() 메소드가 메모리 초과를 유발하는 것일까?

JS의 .sort()메소드는 Timsort알고리즘을 사용한다.

Timsort는 삽입 정렬(Insertion Sort)과 병합 정렬(Merge Sort)의 장점을 결합한 알고리즘이다. 그렇기 때문에 배열의 부분 배열(subarray)을 병합하는 과정이 발생하고 여기서 추가적인 임시 메모리 공간이 필요하게 된다.

Timsort 알고리즘의 동작 원리는 다음과 같다.

1. 부분 배열 생성

   • 배열을 작은 조각들(부분 배열)로 나눈다. 각 부분 배열은 이미 정렬된 상태이다.

     EX) 배열 [5, 3, 1, 7, 6]를 Timsort는 [3, 5]와 [1], [6, 7] 같은 정렬된 부분 배열로 나눈다.
     

2. 부분 배열을 병합

   • 두 부분 배열을 결합하여 정렬된 하나의 배열로 만든다

   • 이때, 병합 작업을 위해 두 부분 배열의 크기만큼의 임시 메모리 공간이 필요하다.

     EX) [3, 5]와 [1] 병합 → 임시 배열 [1, 3, 5] 생성 → 기존 배열에 복사.
     

3. 기존 배열 업데이트

   병합 작업이 완료되면 임시 메모리 공간에 저장된 값을 기존 배열에 복사한다.

위에서 언급한 2번의 과정에서, 병합 과정에 임시 메모리 공간이 필요하기 때문에

.sort() 메소드는 추가적인 메모리 공간 O(N) 을 사용하게 된다.

이걸 모든 반복문 마다 수행하고 있으므로 O(N^2) 만큼의 메모리가 추가적으로 발생하는 것이다.

그래서 메모리 초과가 발생하는 것이다!

여기서 문득 "굳이 우선순위 큐를 사용 할 필요 없이, .sort() 메소드와 비슷한 시간 복잡도에서 메모리 초과만 최적화를 해준다면 우선순위 큐 없이도 이 문제들을 풀 수 있지 않을까?" 라는 생각이 들었다.

메모리 초과를 극복할 수 있는 방법은 다음과 같다.

기존에 .sort() 로 발생한 시간복잡도 O( N * N logN ) 를 조금이나마 줄이고,

메모리의 공간 복잡도 O(N^2)를 최적화하는 것이다.

그래서 생각한 것이 바로 이분탐색 + .splice() 조합이다

결국 필요한 것은 특정 배열에 값을 추가했을 때, 정렬된 상태가 돼야 하는 것이다.

1. 그러므로 먼저 배열에다가 이분탐색을 사용해서 추가할 값에 대한 lowerBound를 구한다.

   이 lowerBound로 잡힌 인덱스가 새로운 값이 들어갈 위치인 것이다.

2. lowerBound로 구해진 인덱스에 .splice() 메소드로 값을 끼워넣는다

이렇게 하면 .sort() 를 사용하여 오름차순 정렬한 것과 동일한 결과를 보장받을 수 있다.

실제 구현 코드는 아래와 같다.

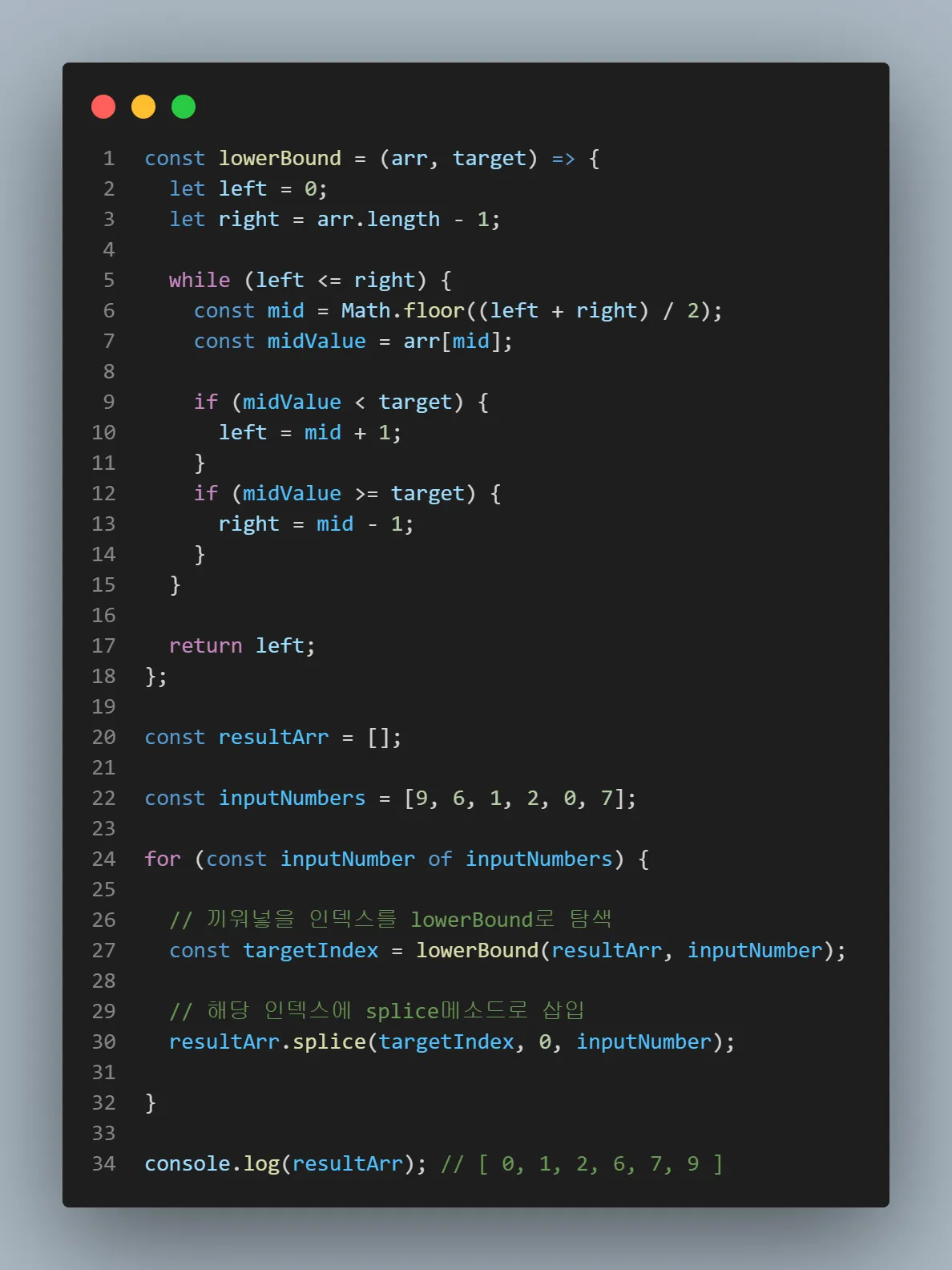
왜 이 방법이 최적화가 되는 것일까?

• 시간 복잡도

  시간 복잡도의 경우 O (N * (logN+N)) ⇒ O(N^2) 이 된다

  .sort()가 O( N * NlogN ) 였던 것을 감안하면 O(N^2) 로 나름 최적화가 됐다.

  물론 앞서 말했듯이 시간 초과가 발생하면 어쩔 수 없이 우선순위 큐를 써야 하므로 시간에 대한 최적화는 크게 신경 쓸 부분이 아니다.
  그러나 이 방법을 사용하면 나름대로의 시간 복잡도 역시 최적화가 가능하다는 것이다.

  
  

• 공간 복잡도❗❗

  기존 .sort()는 정렬된 부분 배열을 병합하기 위해 O(N) 만큼의 새 배열 공간을 임시로 생성해야만 했다.

  그러나 lowerBound로 지정한 위치에 .splice()로 끼워넣을 경우 추가적인 메모리 공간을 사용하지 않을 수 있다.

  .splice() 메소드는 실제로 새로운 배열을 생성하지 않고, 필요한 작업(요소의 추가/삭제)만 기존 배열에서 수정하는 것이기 때문이다.

  즉, 메모리 초과를 여기서 막을 수 있는 것이다.

실제로 기존에 .sort()를 사용했을 때 메모리 초과가 발생했던 로직을 이분탐색 + splice()로 구현했을 때 모두 통과되는 것을 볼 수 있다.

다만 시간은 오래 걸리긴 한다.

예시를 통해 알아보자

가운데를 말해요 문제를 통해 예시를 들어보자.

이 문제를 요약하자면,

1. 각각의 숫자가 입력된다
2. 입력 될 때마다 오름차순으로 정렬하고
3. 그 배열 안에서 중간 인덱스 ( 배열의 길이가 짝수일 경우 2개중 작은 값)를 출력하는 것이다.

예를 들면 아래와 같다.

 (1)
 (1) 5
 1 (2) 5
 1 (2) 5 10
 -99 1 (2) 5 10
 -99 1 (2) 5 7 10
 -99 1 2 (5) 5 7 10

정답 : 1 1 2 2 2 2 5

원래는 이 문제를 풀려면 아래 2개의 우선순위 큐를 써야 한다

• 최대힙 기반의 우선순위 큐
• 최소힙 기반의 우선순위 큐

그러나 구현하기 매우 귀찮기 때문에 .sort() 를 사용하던가, 아니면 이분탐색 + .splice() 를 사용해서 풀어볼 것이다.

.sort()로 구현할 경우

  // BOJ 입출력
  const N = +data.shift();
  const inputNumbers = data.map(Number);

  // 정답 배열
  const result = [];

  // 정렬의 대상이 되는 배열
  const sortedArr = [];

  for (const inputNumber of inputNumbers) {
    // 값을 추가할 때마다 정렬
    sortedArr.push(inputNumber);
    sortedArr.sort((a, b) => a - b);

    const currentLength = sortedArr.length;
    let index = Math.floor(currentLength / 2);
    if (currentLength % 2 === 0) index -= 1;

    // 정답 기록
    result.push(sortedArr[index]);
  }

  console.log(result.join('\n'));

매우 간단하다. 그렇지만 이게 통과가 된다면 골드2라는 난이도가 아니었을 것이다.

바로 메모리초과를 맞게 된다.

이분탐색 + .splice() 조합으로 해결하기

원래는 우선순위 큐를 사용해야 하지만, .sort()에서 발생한 메모리 초과만 해결하면 되므로
이분탐색 + .splice() 조합을 사용해서 아래와 같이 구현할 수 있다.

  // BOJ 입출력
  const N = +data.shift();
  const inputNumbers = data.map(Number);

  // 이분탐색
  const getLowerBoundIndex = (arr, target) => {
    let left = 0;
    let right = arr.length - 1;

    while (left <= right) {
      const mid = Math.floor((left + right) / 2);
      const midValue = arr[mid];

      if (midValue < target) {
        left = mid + 1;
      }
      if (midValue >= target) {
        right = mid - 1;
      }
    }

    return left;
  };

  // 정답 배열
  const result = [];

  // 정렬의 대상이 되는 배열
  const sortedArr = [];

  for (const inputNumber of inputNumbers) {
    // sortedArr에 값을 추가할 때마다 `이분탐색 + .splice()` 적용
    const splicedIndex = getLowerBoundIndex(sortedArr, inputNumber);
    sortedArr.splice(splicedIndex, 0, inputNumber);

    // 정답 기록
    const currentLength = sortedArr.length;
    let index = Math.floor(currentLength / 2);
    if (currentLength % 2 === 0) index -= 1;

    result.push(sortedArr[index]);
  }

  console.log(result.join('\n'));

이 방법으로 .sort()메소드에 비해 추가적인 메모리를 사용하지 않게 되므로 통과하는 것을 볼 수 있다.

낄낄