Big O

minho·2022년 2월 23일

Big O는 왜 필요한가?

하나의 문제에 대해 많은 해결방안이 나온다.
이 해결방안중에서도 좋은 해결방안과 그저그런 해결방안이 있을것이다.
즉, 어떤 해결방안이 좋은지 비교하기 위해서 Big O가 탄생하였다.

Big O는 무엇인가?

코드를 분류하거나 비교할 수 있는 시스템이다.

나의 코드가 어느 분류에 들어갈 수 있는지 Big O를 통해 확인할 수 있다.

ex

n이 주어지면 1부터 n까지 모든 합을 구하는 문제이다.
#1

n = 100000000;
total = 0;

for(let i=1; i<=n; i++){
    total += i;    
}
console.log(total);

결과값
5000000050000000
[Done] exited with code=0 in 1.057 seconds

#2

n = 100000000000;
total = 0;

total = n * (n+1) /2;
console.log(total);

결과값
5000000050000000
[Done] exited with code=0 in 0.077 seconds

#1의 코드는 1.057초가 걸리고 #2의 코드는 0.077초가 걸린다.
이렇게 속도로 비교할 수 있지만, 시간이 별로 차이가 나지않아 어느정도로 차이가 나는지 가늠하기가 어렵다.

우리의 코드를 보고 시간을 측정하지 않고도 어느 코드가 더 좋은 코드인지 평가할 수 있을까?
이럴때 Big O표기법이 유용하다.

Big O는 무엇을 비교하는가?

컴퓨터의 연산갯수를 비교한다.
아까의 코드를 살펴보며 이해해보자.
#2

#2의 코드는 연산이 *,+,/로 총 3개가 있다.
n의 크기와 상관없이 연산은 무조건 3번 이루어진다.

#1

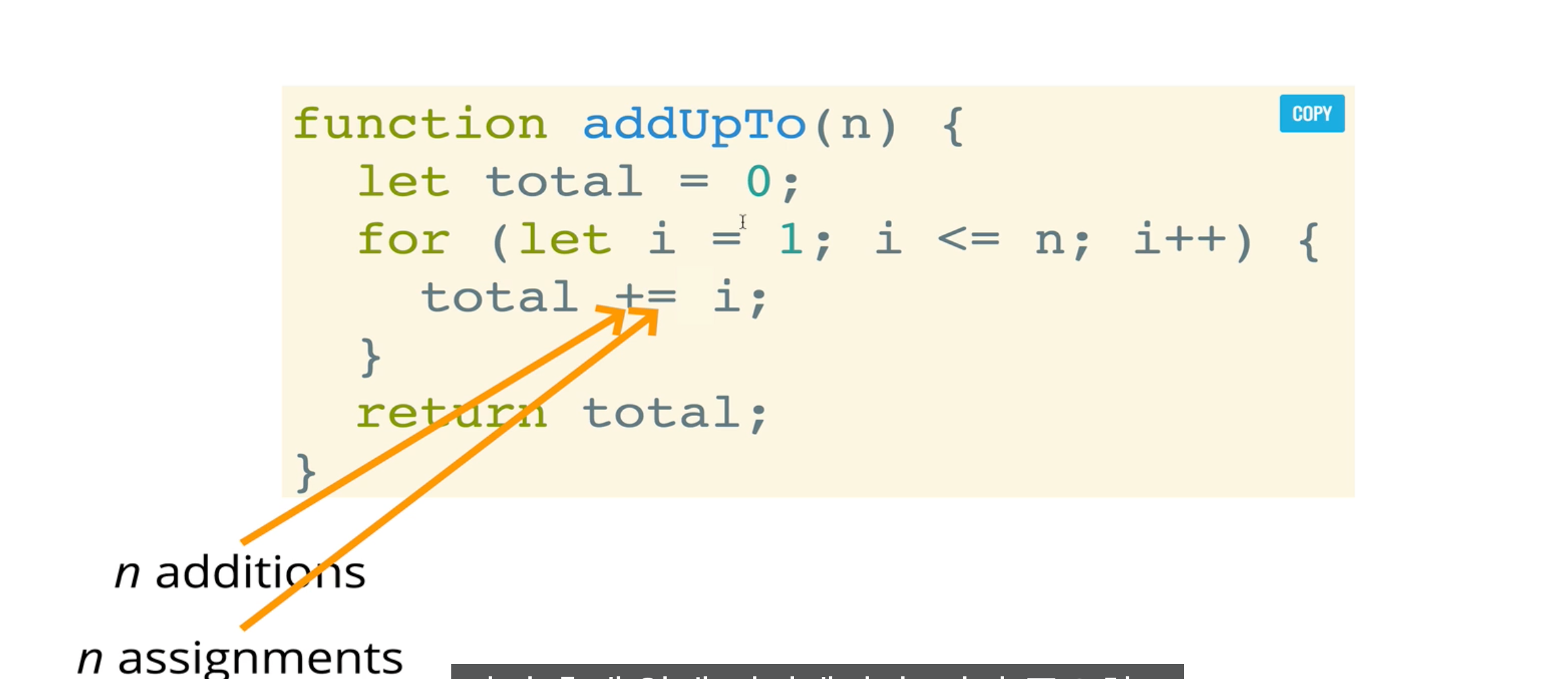
#1의 코드는 어떨까? +가 있으니 연산은 총 1번일까?
for문은 n만큼 반복한다. 그러므로 #1의 연산은 총 n번 실행되는 것이다.
즉 n의 갯수가 늘어날수록 연산이 커진다.

Big O 표기법

Big O의 표기는 실행시간이 갖을 수 있는 최대치이다.

#2와같이 n이 변해도 시간이 변하지 않는다면 f(n)=1이며 O(1)이라고 표시한다.
#1과 같이 n이 변해서 시간이 정비례로 변한다면 f(n)=n이며 O(n)이라고 표시한다.
n이 변하고 시간이 n의 제곱으로 늘어난다면 f(n)=n^2(제곱)이며 O(n^2)이라고 표시한다.

뿐만아니라 n에따라 완전히 다른 표기법이 나타날 수도있다.

ex

function countUpAndDown(n) {
  console.log("Going up!");
  for (var i = 0; i < n; i++) {
    console.log(i);
  }
  console.log("At the top!\nGoing down...");
  for (var j = n - 1; j >= 0; j--) {
    console.log(j);
  }
  console.log("Back down. Bye!");
  
결과값
Going up!
0
1
2
3
4
5
6
7
8
At the top!
Going down...
8
7
6
5
4
3
2
1
0
Back down. Bye!
}

이와같이 for문이 2개면 Big O표기법으로는 O(2n)일까?

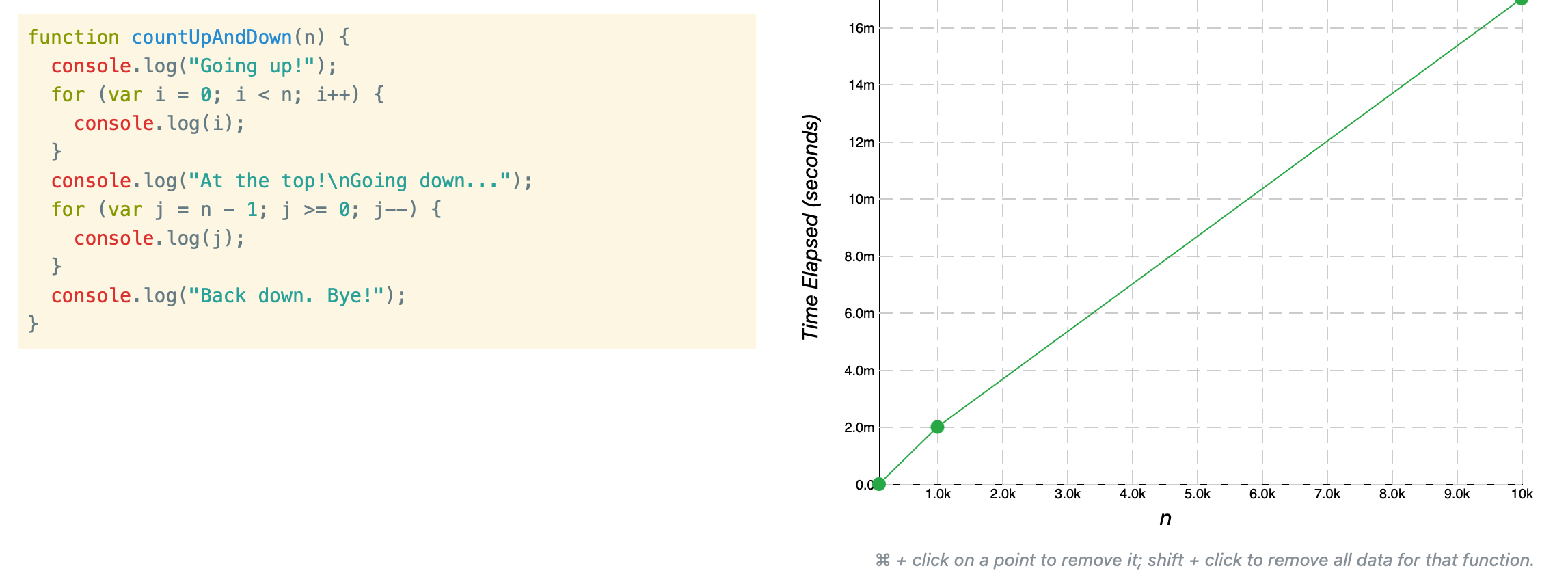
다음의 그래프는 n에 100,1000,10000을 입력했을때 속도의 그래프이다.
결국 n만큼 연산하므로 정비례 그래프를 나타내는것을 알 수 있다.
그러므로 for문이 두개여도 O(n)으로 나타낸다.

그러나 위와같이 for문이 중첩으로 되어 있으면 n의 제곱이다.
첫번째 for문의 i가 오고 j가 다 돌고 나서야 다음 i로 넘어갈 수 있기 때문이다.
그러므로 중첩이 있으면 Big O는 O(n^2)이다.

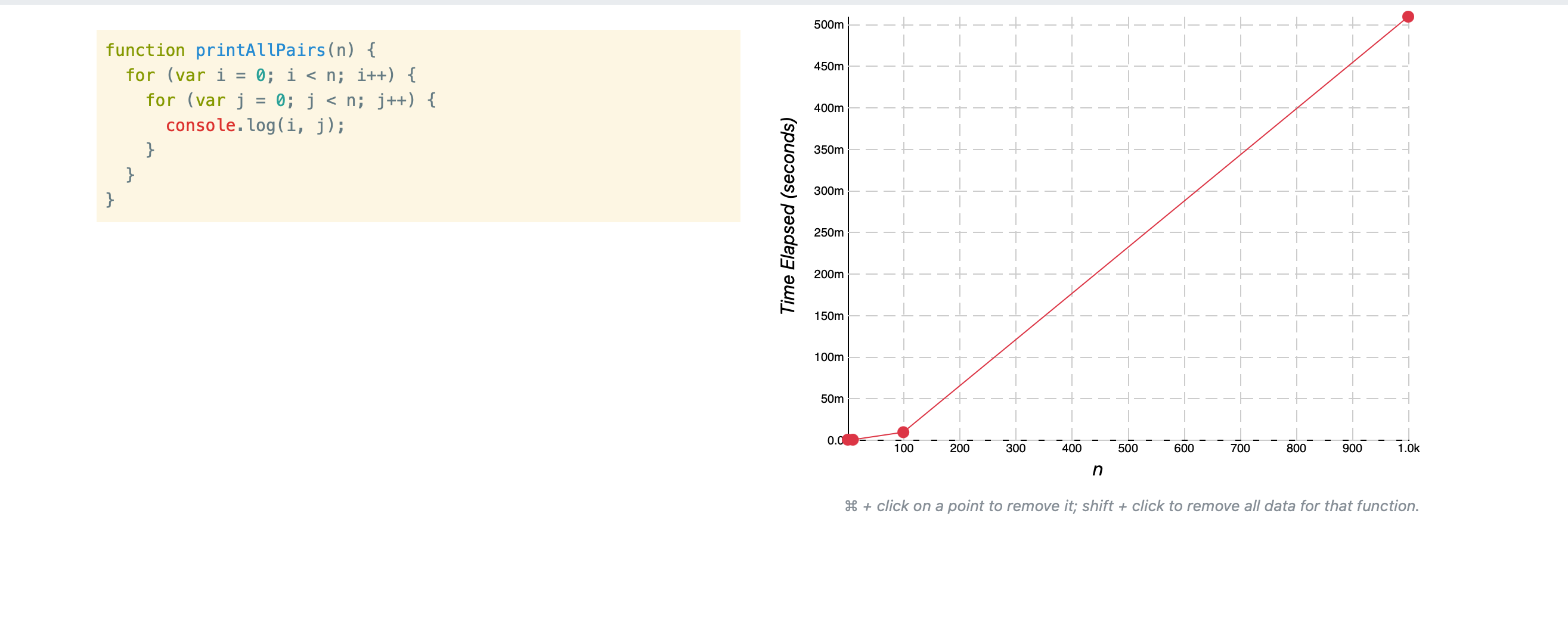
위와같이 작업시간이 기하급수적으로 늘어나는 것을 볼 수 있다.

공간복잡도

constant(상수)
불리언, 숫자, undefined, null등은 javascript에서 모두 불변의 공간이다.
그러므로 공간복잡도는 무조건 1이다. => O(1)
문자열
문자열은 문자열의 길이만큼 공간복잡도가 커진다.
문자열의 길이가 n이라면 공간복잡도는 O(n)이 된다.
이와 마찬가지로 배열(array)도 배열의 길이(n)만큼 O(n)이 된다.
참조타입(reference type)
참조타입인 객체의 경우는 key의 갯수(n)에 따라 공간복잡도가 결정될 수 있다.