동적계획법이란?

• 특정 범위까지의 값을 구하기 위해 이전 범위의 값을 활용하여 효율적으로 값을 얻는 기법
• 이전 범위의 값을 저장함으로써 시간적, 공간적 효율을 얻음

점화식

• 인접한 항들 사이의 관계식
• 동적 계획법 문제를 풀 때는, 점화식을 미리 세우고 풀면 좋다.
• 이전 값들을 통해 DP(현재)를 정의하자.

계단오르기(예시문제)

어떻게 관계식을 정의할 것인가?

우리가 알 수 있는것은 1칸을 올라가는 것은 1가지 방법뿐이고 2칸을 올라가는 것은 2가지 방법이다.
그러므로 dy[1]=1, dy[2]=2를 표시해준다.


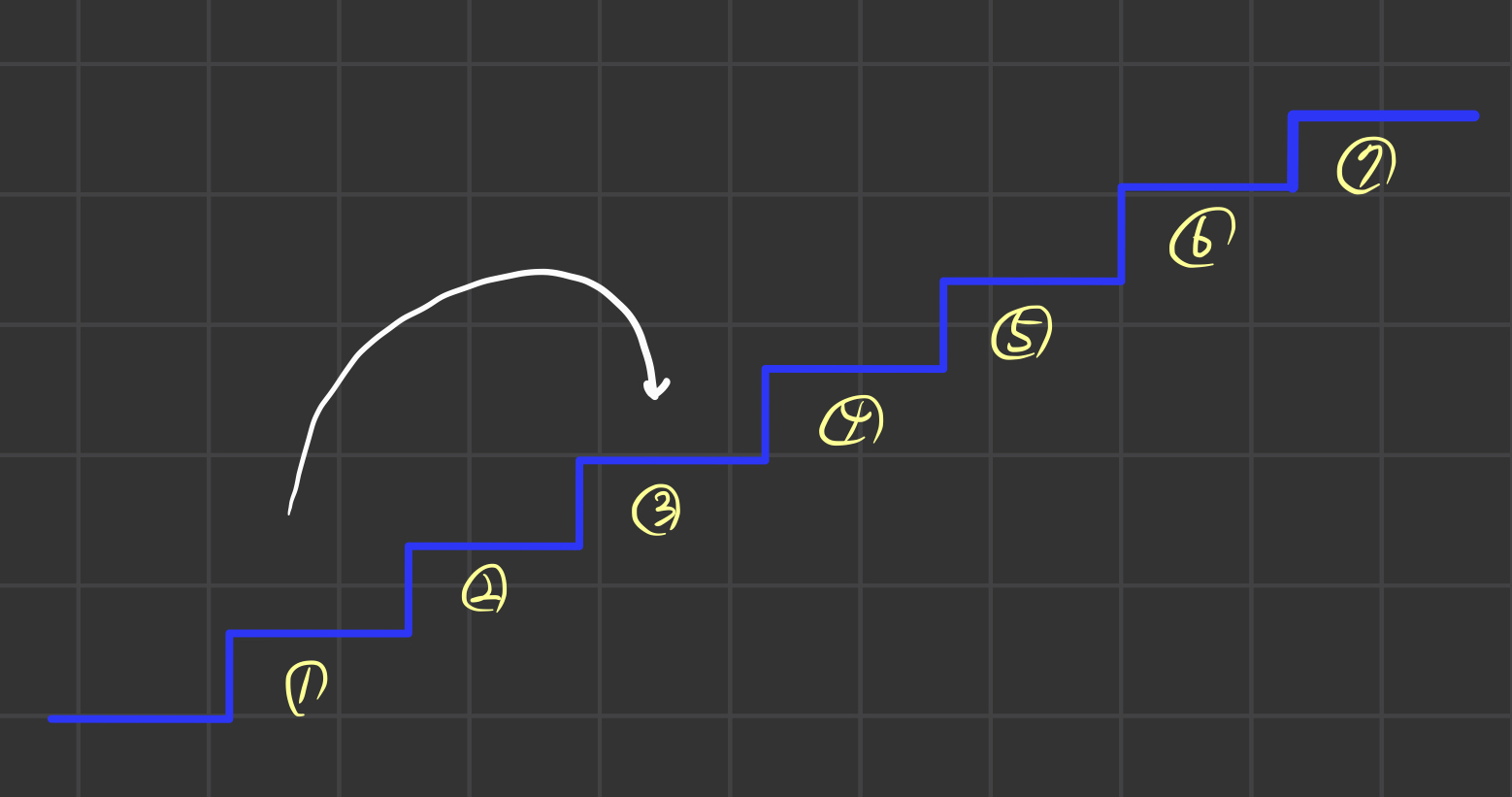
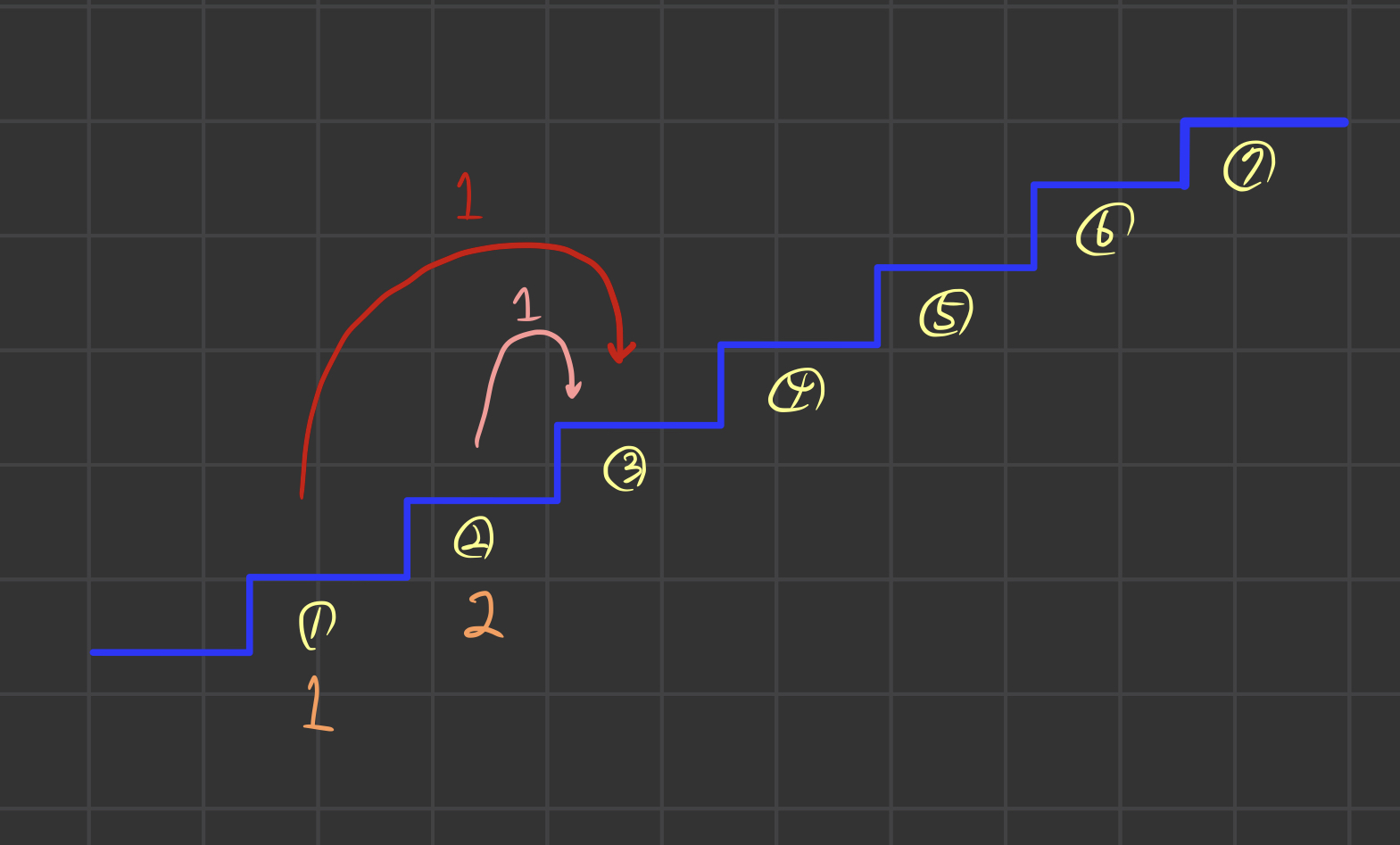
그렇다면 3칸을 올라가는 방법을 살펴보자
1에서 3으로 가려면 2칸을 올라가는 한가지방법밖에 없다.
1칸으로 올라가는 방법이 1가지이고 3으로 올라가는 방법도 1가지 이므로 0에서 1을커쳐 3으로 가는 방법은 1가지이다.
마찬가지로 2로 가는 방법이 2가지이고 2에서 3으로 올라가는 방법이 1가지 이므로 0에서 2를거쳐 3으로 가는 방법은 2가지이다.

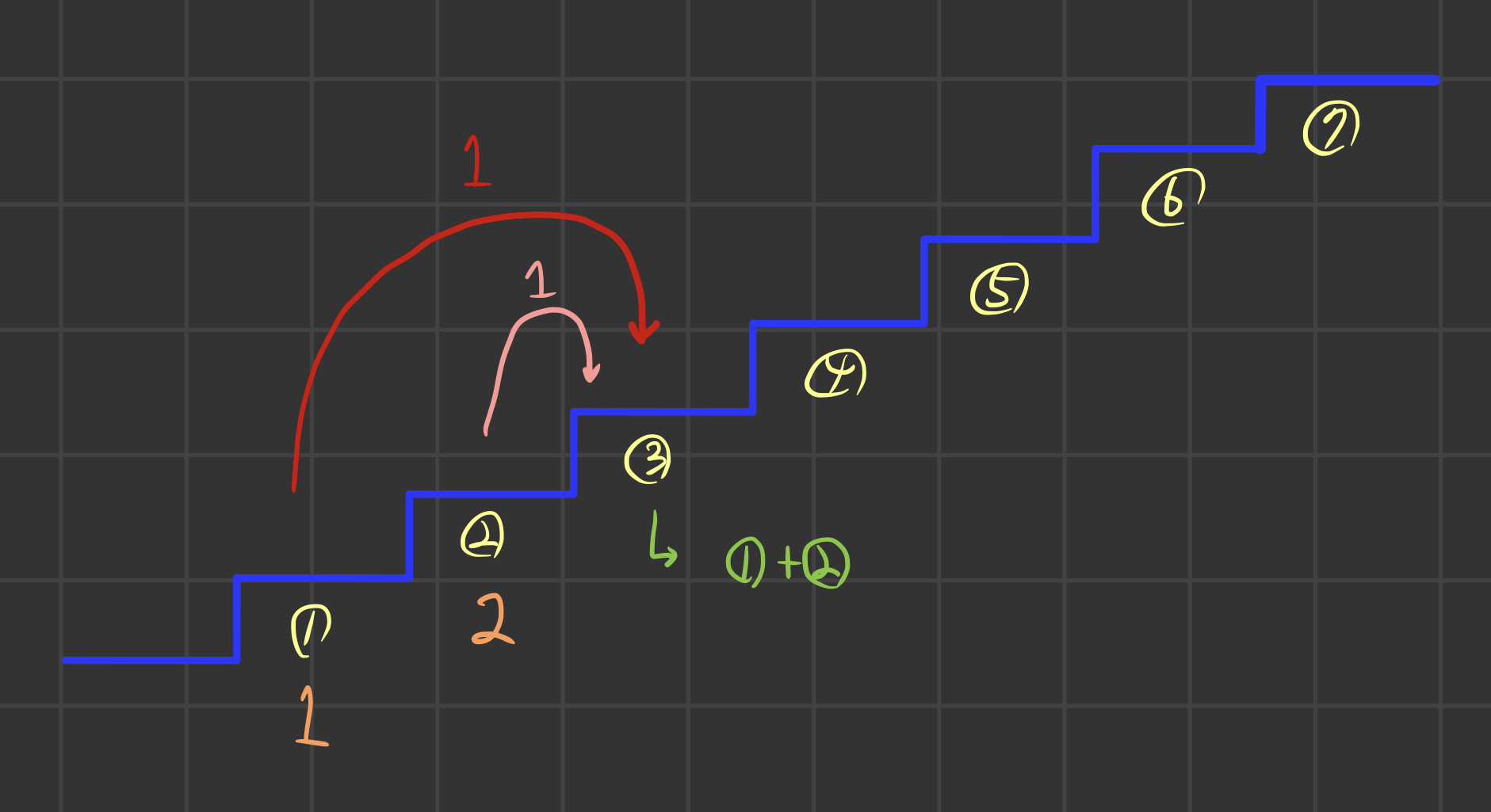
3으로 가는 방법은 dy[3-1] + dy[3-2]라는 걸 알 수 있다.

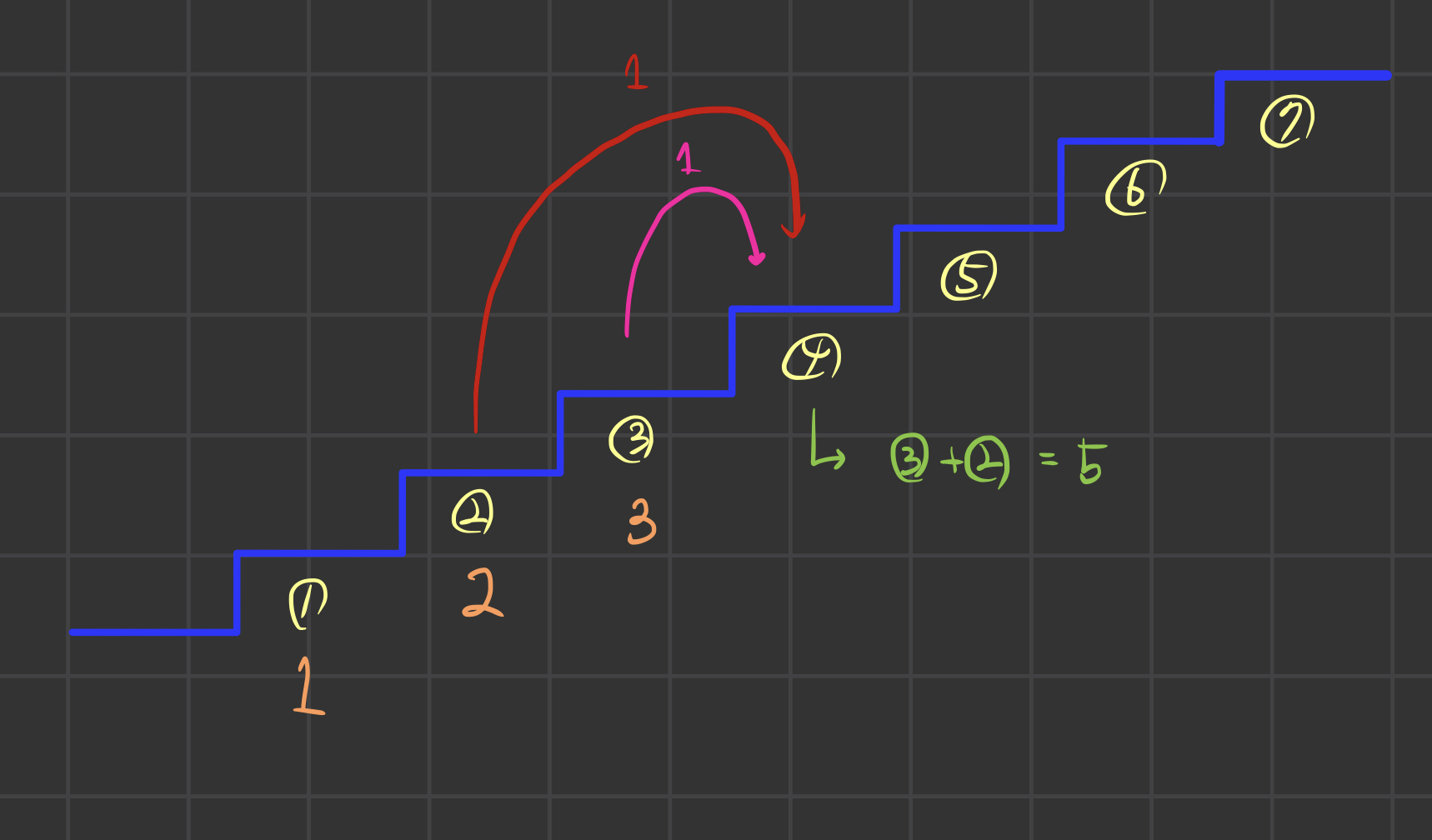
0에서 4로 가는 방법도 마찬가지이다.
2로 갈수있는 가짓수와 3으로 갈 수 있는 가짓수를 합치면 4로 가는 가짓수가 된다.
결국 점화식을 구해보자면

dy[n] = dy[n-1] + dy[n+1]이다.

이것을 이용하여 코드를 구성하면 아래와 같다.

function solution(n){  
    let answer=0;
    let dy = Array.from({length: n+1} ,()=>0);
    dy[1]=1;
    dy[2]=2;
    for(let i=3; i<n+1; i++){
        dy[i]=dy[i-1]+dy[i-2]
    }
    answer = dy[n];
    return answer;
}
console.log(solution(7)); //21