수열 추측하기(순열, 이항계수 응용)

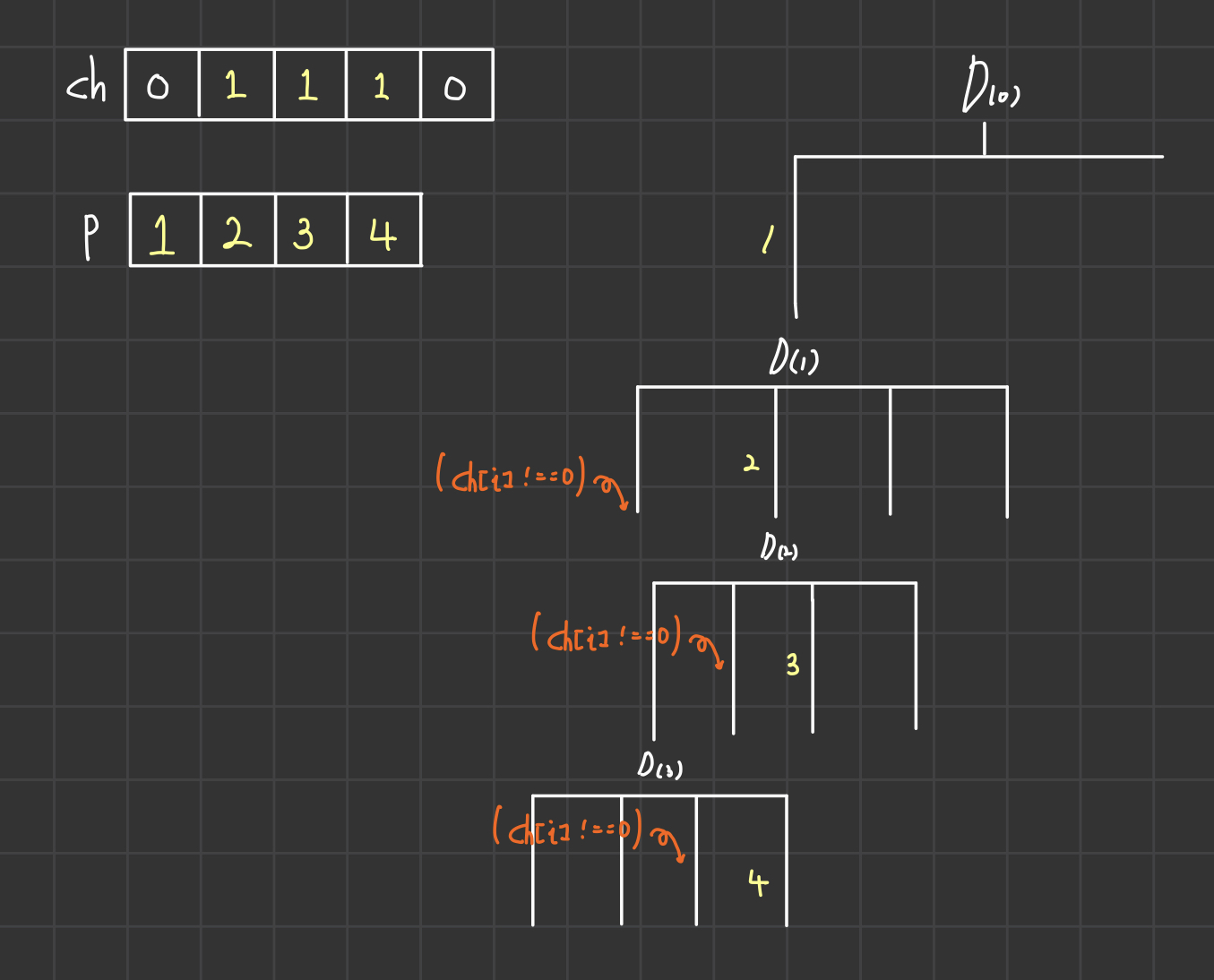
순열의 원리

[1, 2, 3, 4] 4개의 숫자로 4자리 모든 경우의 수를 알아보는 방법 (단, 숫자는 중복되지 않는다.)

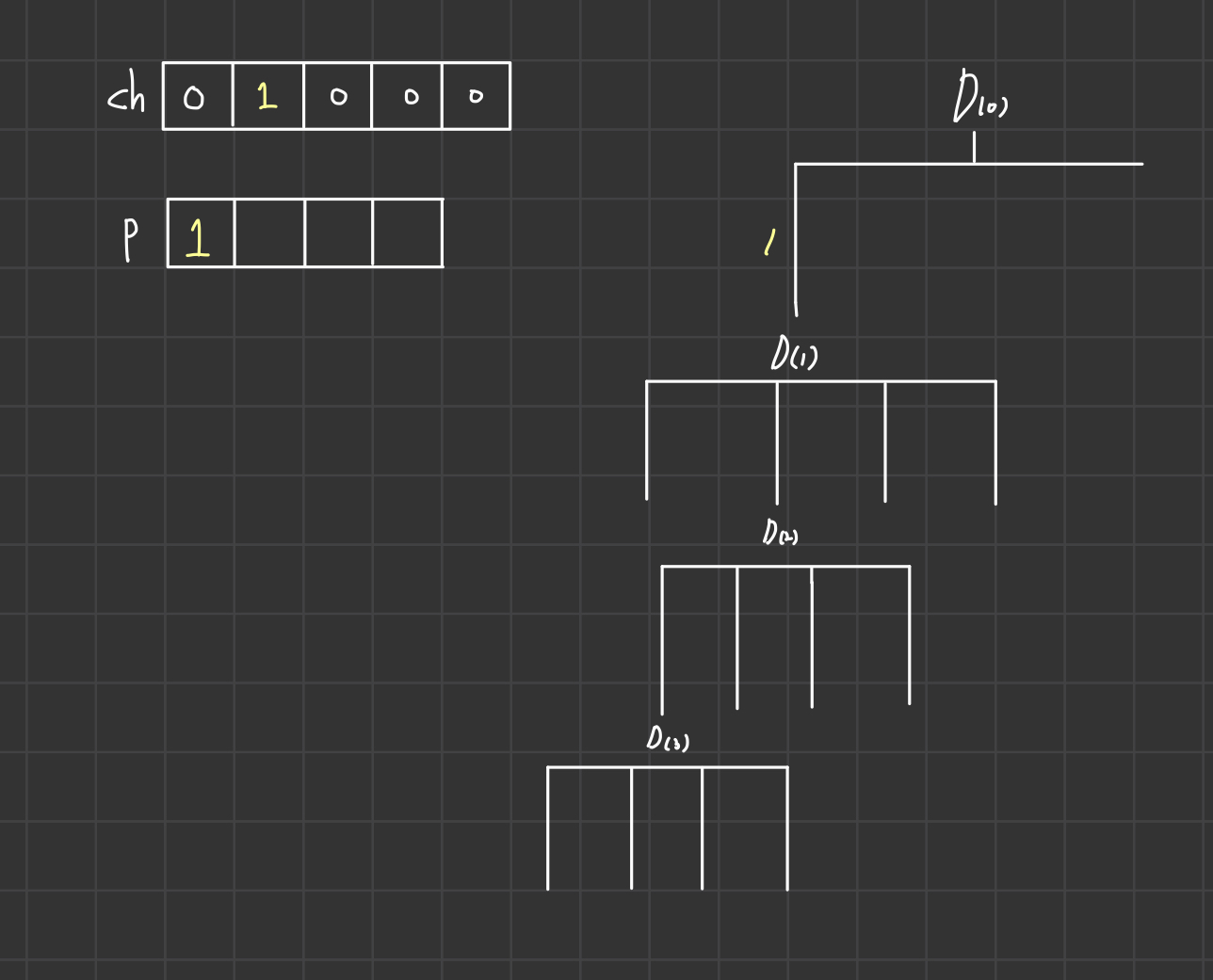
D(0)에서 4개중에 1개의 숫자를 선택한다. 여기서는 1을 선택했다.
ch는 check라는 뜻으로 1이 포함되었는지 아닌지 확인해주기 위해 ch[1]에 1로 포함되었다고 표시해준다.(0은 포함되지 않았다는 뜻이다.)
배열 p는 4자리 숫자의 조합으로 여기서 1의 자리 숫자는 1로 표시한다.

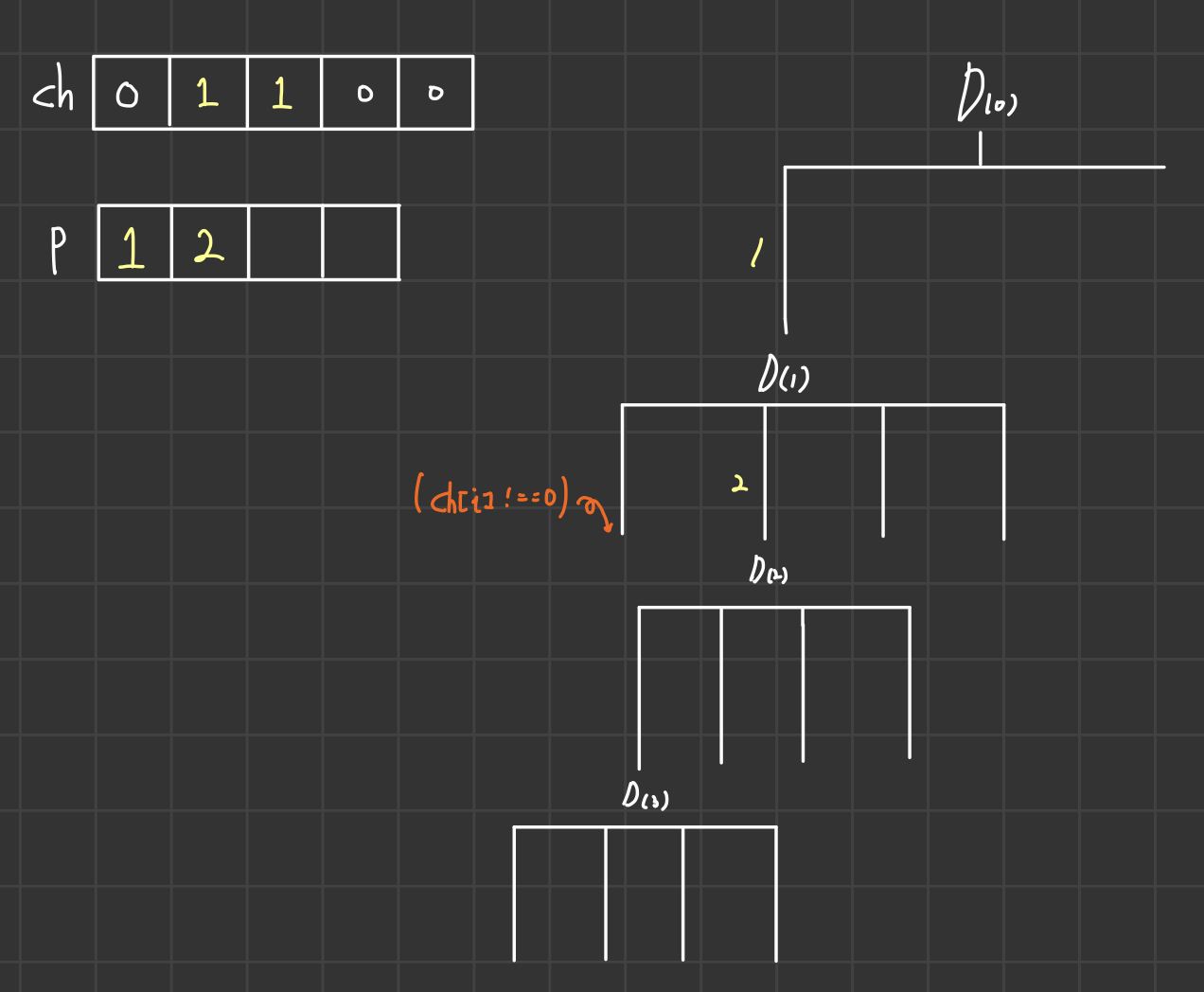
다음 D(1)로 넘어가서 1은 이미 ch[1]에 포함되었다고 표시했기 때문에 2로 넘어간다.
위와 마찬가지로 ch[2]와 p의 둘째자리에 표시해준다.

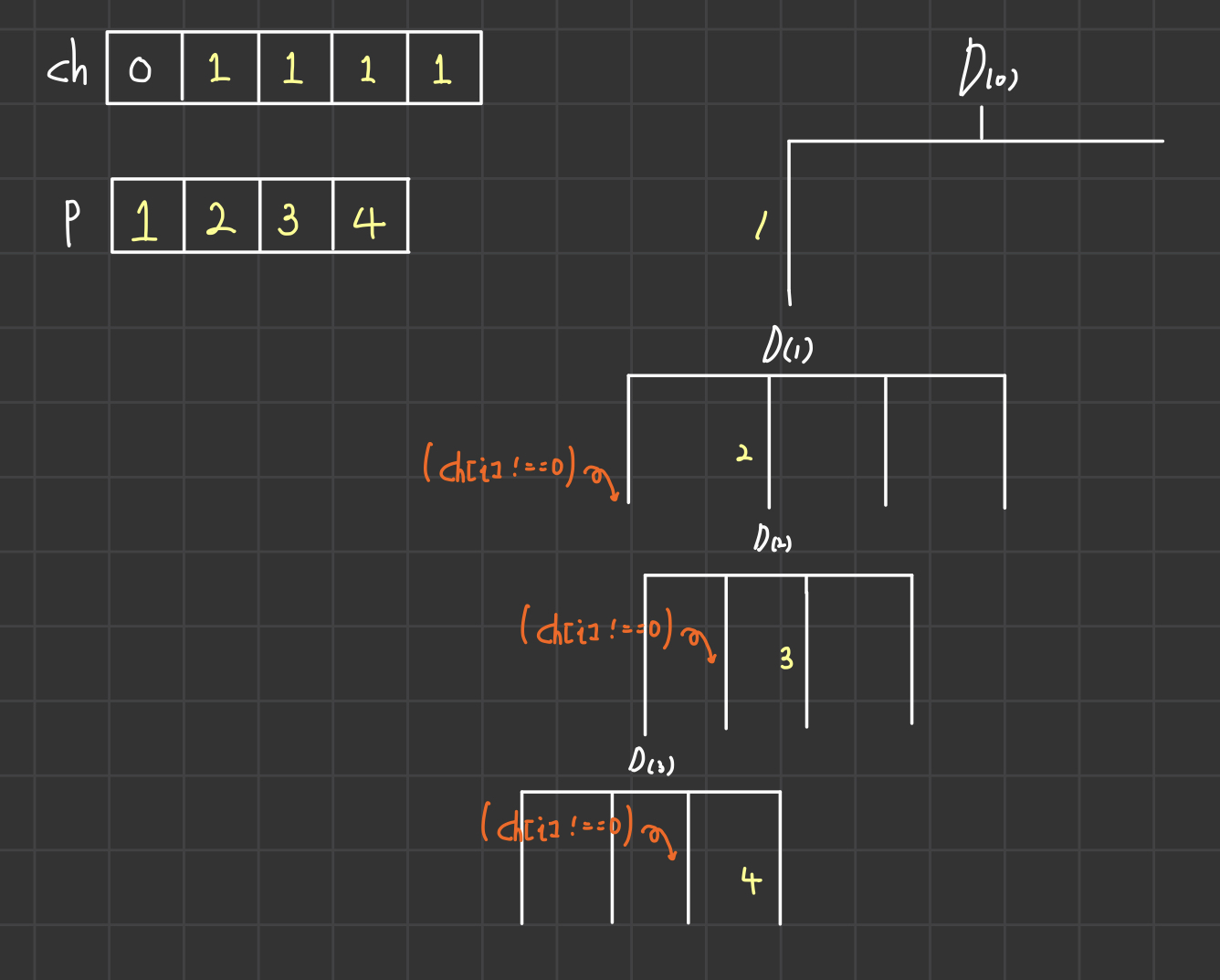
이런식으로 p의 넷째자리 숫자까지 모두 표시해준다.
p의 네자리가 모두 있으므로 answer에 p의 값을 넘겨준다.

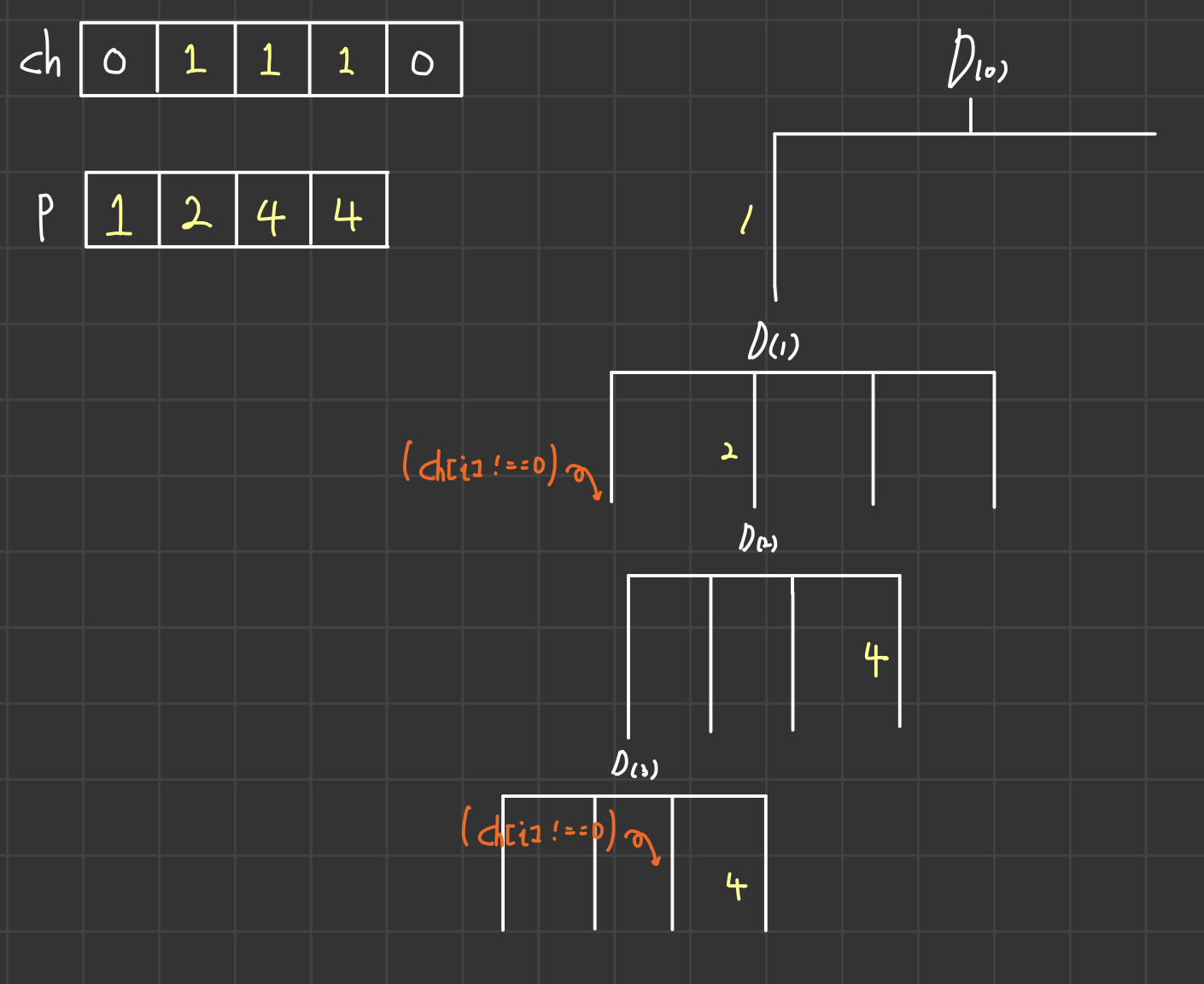
그후 다시 D(3)으로 올라가기 전에 D(3)에서 썻던 숫자는 다른 자리에서 써야 하므로 ch[4]를 0으로 해준다.

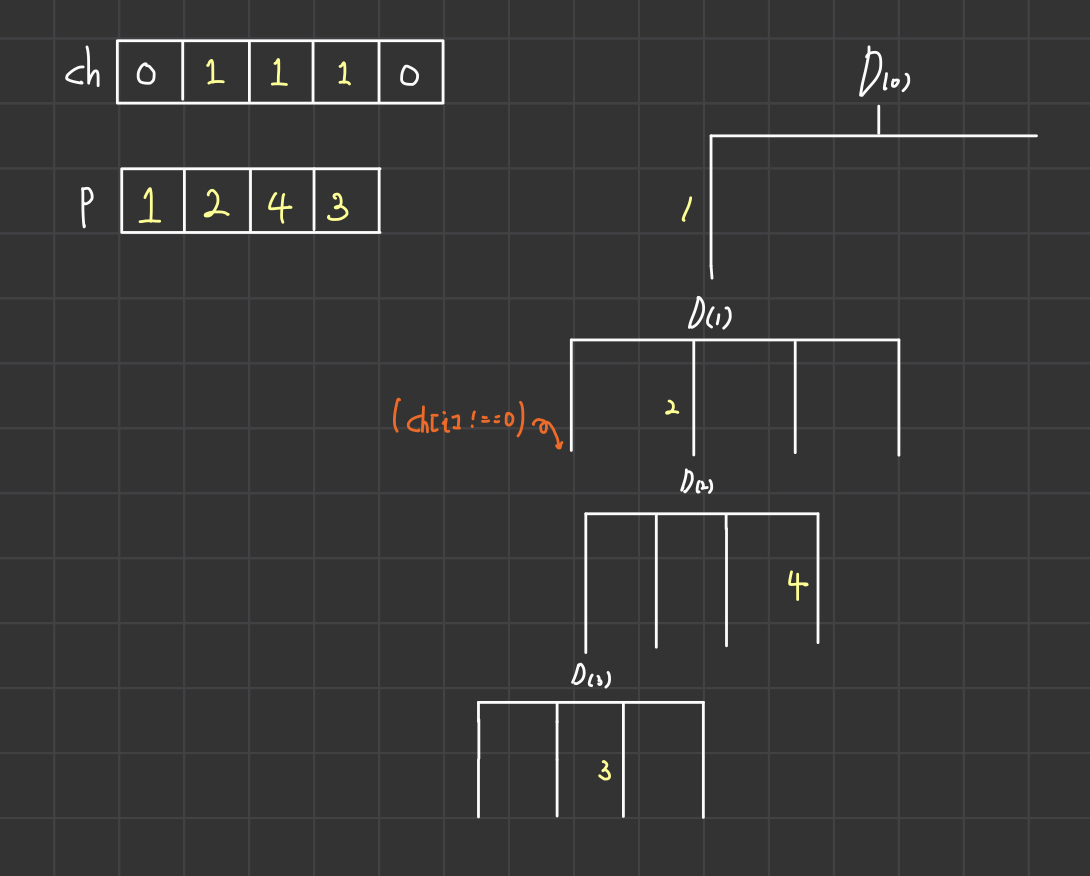
그리고 D(3)으로 올라가서 ch에서 사용가능한 숫자를 찾은 후에 그 숫자로 바꾸어 준다.

이런식으로 올라갔다 내려갔다를 반복하여 모든 수의 조합을 만들 수 있다.

문제풀이

이 문제는 저 순열의 원리와 메모지에이션 방법을 혼합해 문제를 풀 수 있다.
메모지에이션 원리: https://velog.io/@minho100227/조합수메모이제이션

코드

function solution(n, f){         
        let answer, flag=0;
        let dy= Array.from(Array(11), () => Array(11).fill(0));
        let ch=Array.from({length:n+1}, ()=>0);
        let p=Array.from({length:n}, ()=>0);
        let b=Array.from({length:n}, ()=>0);
        function combi(n, r){
            if(dy[n][r]>0) return dy[n][r];
            if(n===r || r===0) return 1;
            else return dy[n][r]=combi(n-1, r-1)+combi(n-1, r);
        }
        function DFS(L, sum){
            if(flag) return;
            if(L===n && sum===f){
                answer=p.slice();
                flag=1;
            }
            else{
                for(let i=1; i<=n; i++){
                    if(ch[i]===0){
                        ch[i]=1;
                        p[L]=i;
                        DFS(L+1, sum+(b[L]*p[L]));
                        ch[i]=0;
                    }
                }
            }
        }
        for(let i=0; i<n; i++){
            b[i]=combi(n-1, i);
        }
        DFS(0, 0);
        return answer;

여기서 요점은 sum이 f에 해당하는 값과 일치할때의 p값이므로
if(sum === f)일때 answer값을 p값으로 바꾸고 flag에 값을 줘서 DFS에서 빠져 나오게 하는 것이다.