조합수(메모이제이션)

개념설명

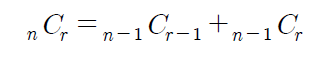
먼저 위의 사진을 이해해보자
만약 n=5이고 r=3을 예시로들면 아래의 사항을 의미한다.

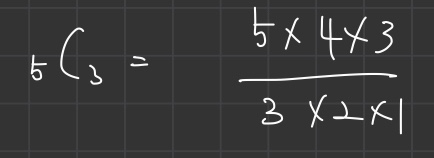
즉, 5개중 3개를 뽑는 방법이다.
중복되는 수 없이 5개중에 3개를 뽑으므로 밑의 3x2x1을 나누어 주는 것이다.

그렇다면 위의 식이 어떻게 성립하는 것일까?

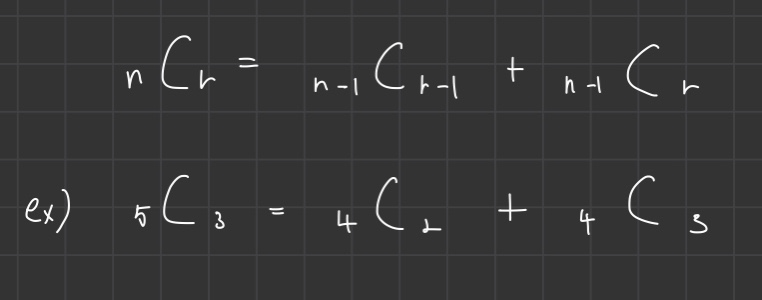
n=5이고 r=3을 예시로들면 위의 사항대로 된다.

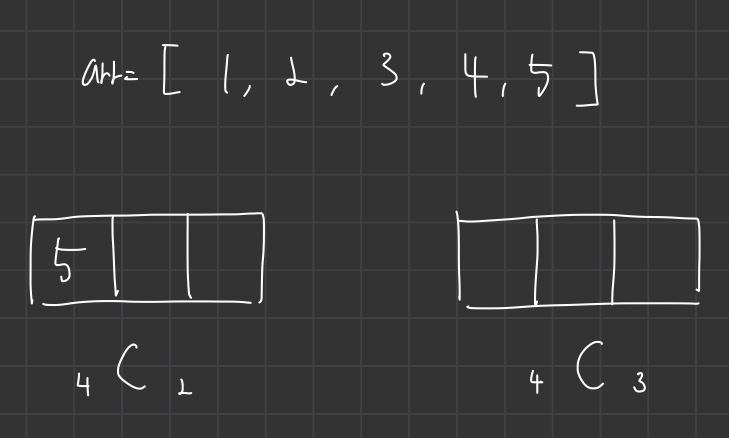
그 이유는 경우의 수를 두가지로 나눌 수 있기 때문이다.
예를들어 5를 꼭 포함하는 경우 3개의 숫자를 조합한다면 4개의 숫자중에 2개숫자만 조합하는 것을 뜻한다.
반대로 5를 무조건 포함시키지 않는 경우는 4개의 숫자중 3개의 숫자를 조합하는 것을 뜻한다.
결국 이 둘을 더하면 5개의 숫자중 3개를 조합하는 것과 같은 것이다.

그렇다면 위의 식을 DFS로 표현하면 어떻게 될까?

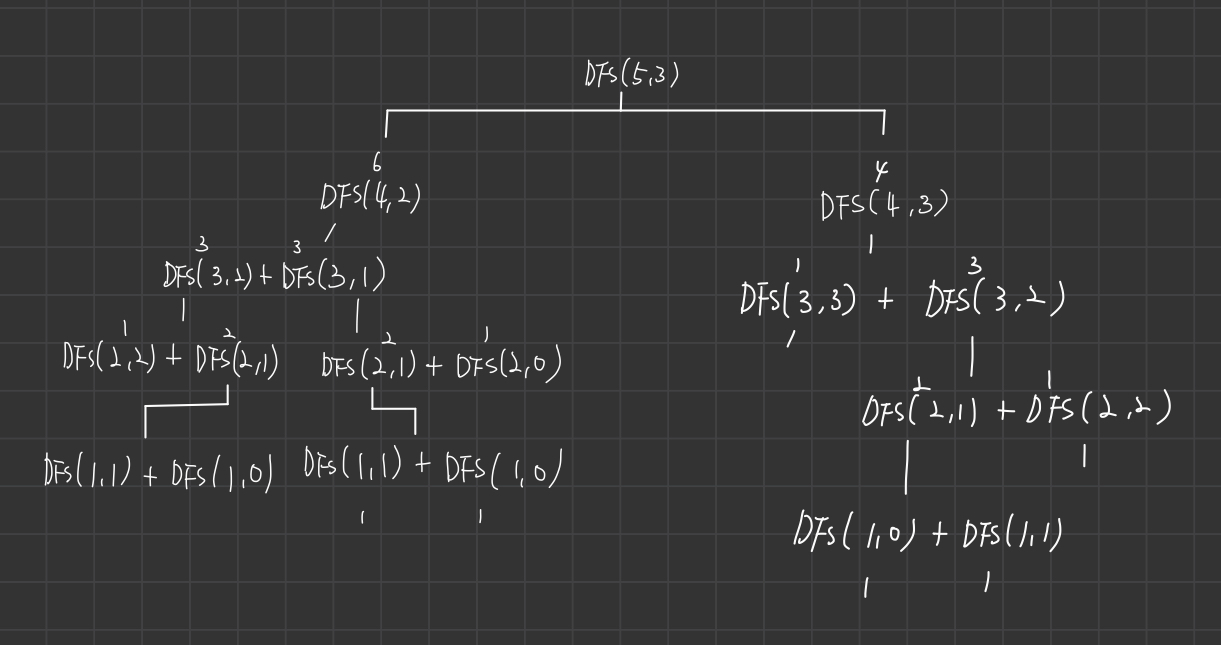
n=r 이거나 r=0이면 경우의 수는 1개밖에 되지 않는다.
DFS(3,3)은 3개중 3개를 뽑으라는 말이므로 당연 경우의 수는 1이다.
DFS(1,0)은 1개중 0개를 뽑으라는 말이다.
조금 헷갈릴 수도 있지만 0개를 뽑는것은 아무것도 안뽑는다는 경우의 수에 들어가므로 경우의 수는 1이다.

그렇다면 이를 코드로 구현해보자.

function solution(n, r){         
        let answer=[];
        function DFS(n, r){                
            if(n===r || r===0) return 1;
            else return DFS(n-1, r-1) + DFS(n-1,r);                    
        }
        answer=DFS(n, r);
        return answer;
    }
	console.log(solution(5, 3));

n=r 이거나 r=0이면 1을 반환해서 재귀함수를 끝내주고
그렇지 않다면 계속 밑으로 내려가야 하므로 n과 r의 숫자를 각각 빼준다.

그러나 이 코드는 문제점이 있다.
n과 r이 5와 3으로 숫자가 작을때는 문제가 없지만, 30, 25 이정도의 숫자가 되면 밑으로 뻗어가는 수들이 어마어마하게 많아진다.
즉, 효율성 문제가 생긴다.

어떻게 효율성 문제를 해결할까?

이를 해결하기위해 메모지에이션을 사용한다.
메모이제이션이란 각각의 DFS의 결과 값들을 다른 공간에 저장시켜두어 같은 DFS가 반복되었을때 그 값을 가져오는 것을 말한다.

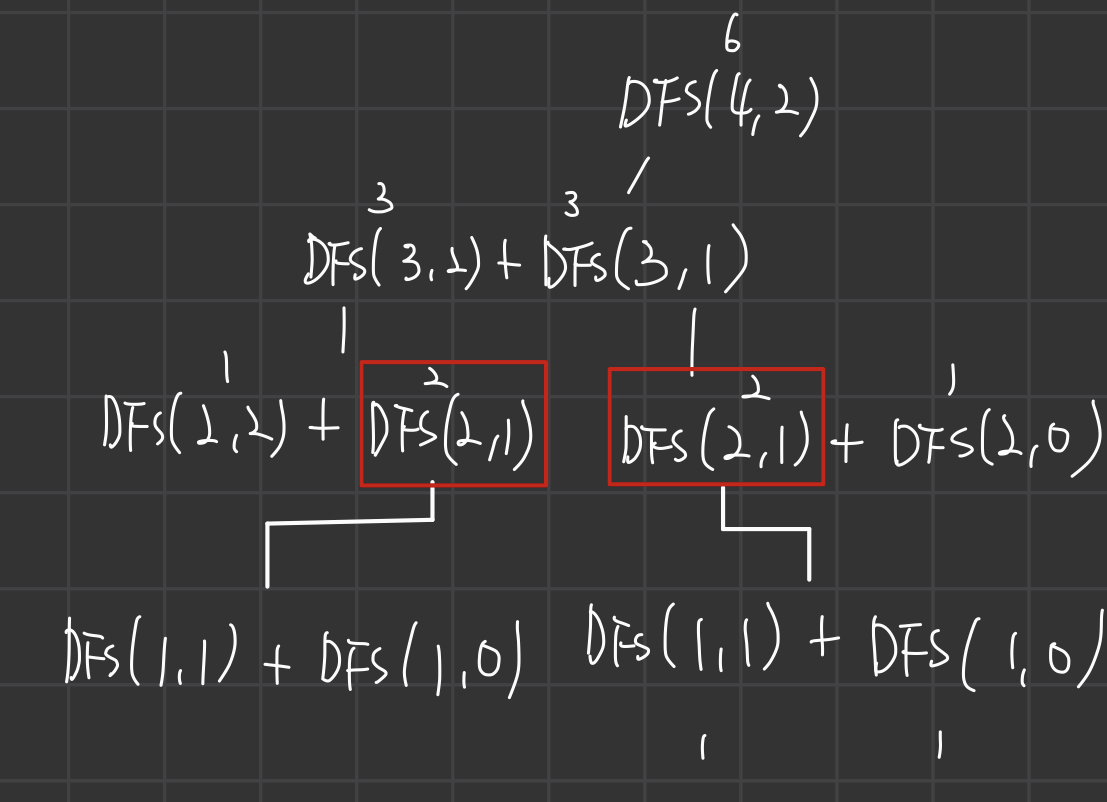
예를들어 왼쪽 DFS(2,1)을 다 처리한후 2라는것을 알았다.
그 후 오른쪽에 같은 DFS(2,1)이 나왔을때 굳이 밑으로 또 뻗어나가야 할까?
즉, 메모지에이션을 통해 똑같은 DFS라면 더 밑으로 내려가지 않고도 값을 알 수 있어 시간을 단축 시킬 수 있다.

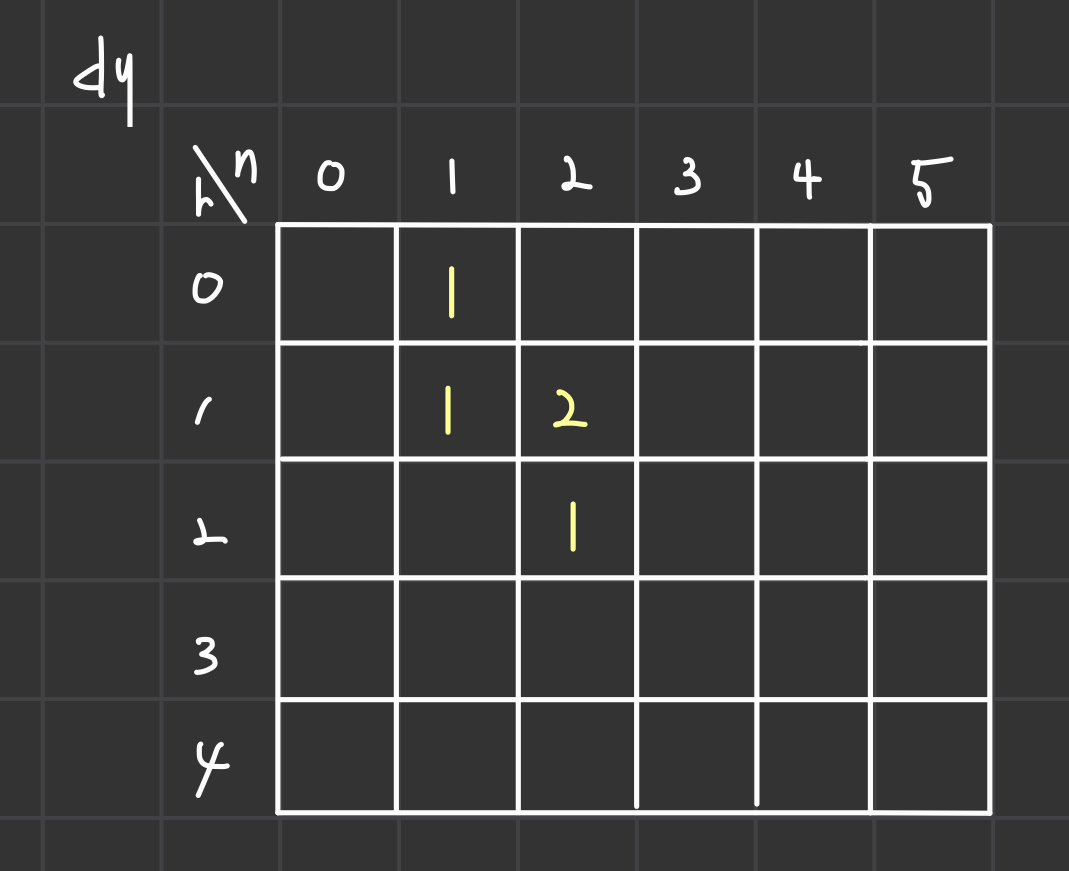
위와같이 dy에 값들을 저장시키고 불러온다.
dy[n][r]로 구성되어 있다.

그렇다면 이를 코드로 구현해보자.

function solution(n, r){         
        let answer=[];
  	let dy = Array.from(Array(35), ()=> Array(35).fill(0));
        function DFS(n, r){ 
            if(dy[n][r]>0) return dy[n][r];
            if(n===r || r===0) return 1;
            else return dy[n][r] = DFS(n-1, r-1) + DFS(n-1,r);                    
        }
        answer=DFS(n, r);
        return answer;
    }
	console.log(solution(5, 3));

dy[n][r]에 값이 있으면 dy[n][r]를 반환해주고, 없으면 dy[n][r]에 값을 넣어준다.