ResNet 논문을 읽고 헷갈렸던 부분, 조원과 멘토님과 이야기했던 부분을 정리한다.

Main Idea

ResNet은 매우 깊은 모델에서 optimize를 쉽게 하기 위해 고안되었다. Gradient vanishing으로 생기는 degradation 문제를 해결하기 위해 Residual Block을 사용한다.

18 layer와 같이 너무 깊지 않은 모델의 gradient vanishing 문제는 normalized initialization, intermediate normalization layer를 사용하면 해결할 수 있다. 그러나 50, 101, 152 layer 처럼 너무 깊어지면 gradient vanishing 문제가 발생하고 학습이 되지 않아 성능이 떨어지는 Degredation 문제가 여전히 발생한다. 이를 해결하기 위한 방법으로 Residual learning framework를 제시한다.

Residual Block

Residual은 관측값과 예측값의 차이를 의미한다.

Residual Block 구조

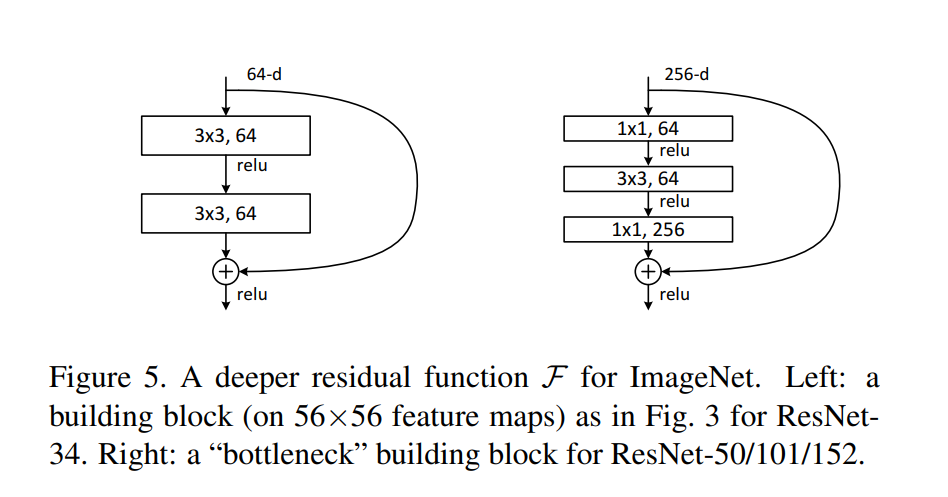
여러개의 층으로 이루어진 block의 입력이 x, 출력이 $H(x)$리고 하자. Residual을 사용하지 않는다면 block 내부의 multi layers가 학습해야 하는 것은 $H(x)$ 이다. 그러나 Residual Block에서는 $H(x) - x$인 $F(x)$만 학습하면 된다. Residual인 $F(x)$만 학습하므로 Residual learning이라고 하는 것 같다.

효과

Residual block은 그냥 일반 block보다 $H(x) = x$인 Identical mapping을 학습하기 쉽다. 왜냐하면 multi layer의 weight를 0으로 보내서 $F(x)$를 0으로 만들면 Identical mapping이 되기 때문이다. $H(x) = x$가 되는 weight를 찾아야 하는 일반 block에 비해 쉬울 수 밖에 없다.

Identity mapping이 우리가 학습하고자 하는 Optimal functin인 경우는 거의 없다. 그러나 저자들은 학습이 끝난 후 Optimal한 H(x)는 0보다는 x에 가까울 것이라고 추측한다. 처음부터 x와 비슷한 값을 만들기 위해 학습하는 것보다 Residual block을 사용하여 Identical mapping에서 조금만 값을 변경하는 것이 더 쉽다는 것이다. 이를 논문에서는 precondition을 제공한다고 표현하였다.

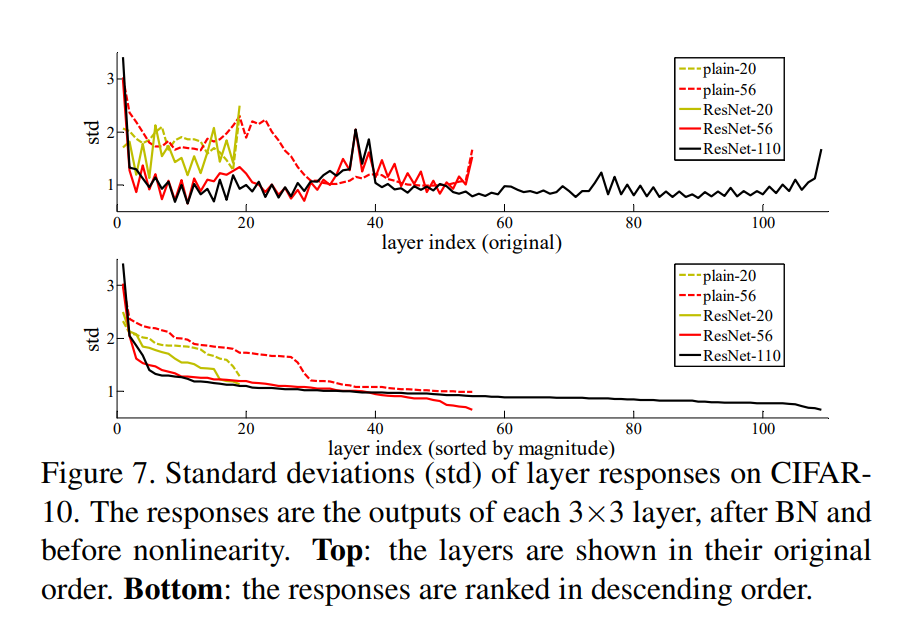
위에서 Optimal function이 Identity mapping에 가깝다는 가정을 뒷받침 할 수 있는 자료이다. 학습이 끝난 후 각 layer 별로 F(x)의 표준편차을 계산한 그래프이다. F(x)는 Batch normalization을 사용하여 평균이 0이므로 표준편차가 작다는 것은 0에 가까운 값이 많다는 것을 의미한다. 전체적으로 ResNet의 표준편차가 작은 것으로 봐서 학습해야 하는 Optimal function이 Identity mapping에 가깝고 위에서 예상한 것처럼 Residual Block이 resonable한 precondition을 제공한다는 것을 알 수 있다.

Gradient 전달

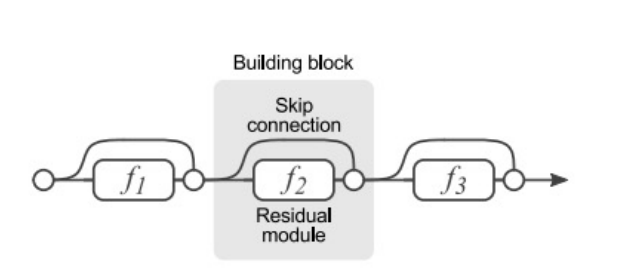
Residual Block을 Gradient 전달 관점에서 생각하면 block 내부의 layers를 거치지 않고 바로 gradient가 전달 될 수 있는 지름길 (shorcut connection)을 만들어 주는 것이다. 이를 통해 Gradient vanishing 문제를 어느 정도 해결할 수 있다. Residual Block을 추가할 때마다 2n개의 gradient 전달 경로가 생긴다.

Ensemble

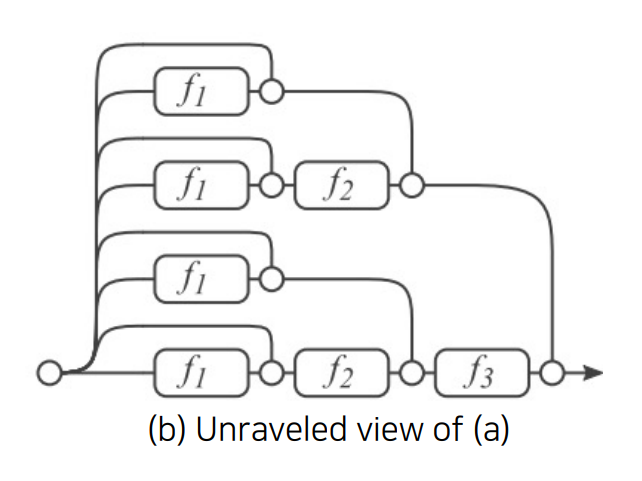
Residual block을 사용하면 입력이 출력으로 가능 방법이 F(x)를 거치는 방법과 안거치는 방법 2가지가 있다. 모든 방법을 표현하면 위의 그림과 같아진다. 각 방법을 하나의 모델이라고 생각하면 여러 모델을 ensemble하는 효과로도 생각할 수 있다고 한다.

Batch Normalization

본 논문에서는 이유는 서술하지 않았지만, 학습 과정에 Dropout을 사용하지 않았다고 언급하고 있다. Batch normalization을 사용하면 Dropout을 사용하지 않아도 된다고 한다. Batch normalization은 평균이 0이 되도록 정규화를 한다. 이때 0에 가까운 값들이 많이 생기고 마치 dropout과 같은 효과를 낼 수 있기 때문이다.