🐤 서론
엄청 오랜만에 블로그를 쓰는 것 같다.
이렇게 글로 쓰는 것도 오랜만이지만, 공부의 흔적을 남기고 제대로 더 열심히 취준하기 위해서 습관을 들여야할 것 같다!
오늘부터 SSAFY가 거의 끝나고 알고리즘 공부를 빡세게 해야할거 같아서 시작했다.
인프런에 있는 강의인 큰돌님의 10주완성 C++ 코딩테스트의 커리큘럼을 혼자 따라갈 예정이다.
C++이고 가격이 조금 나가서 구매하지는 않았지만 백준 문제집에 문제들은 있어서 이거 보고 따라가기로 했다!
이 강의는 160문제를 추천해주는데 문제 자체가 많아서 좋은 것같다.
그치만, 백준 문제집에 1~2주 이렇게 묶여 있어서 알고리즘마다 찾기 쫌 힘들다..ㅠㅠ
그래서 기본적인 알고리즘 문제는 구글링해서 찾아서 풀면서 개념 익히고, 추가로 큰돌님 문제집을 풀려고 한다.
< 큰돌님 커리큘럼은 이러하다 >

내가 C++로 준비를 했으면 결제를 했을듯 하다!
혹시 C++로 준비를 하는 사람이라면 고민해보길 바란다.
https://www.inflearn.com/course/10%EC%A3%BC%EC%99%84%EC%84%B1-%EC%BD%94%EB%94%A9%ED%85%8C%EC%8A%A4%ED%8A%B8-%ED%81%B0%EB%8F%8C
🐤 누적합 개념
🍡 누적합 언제 배웠지??
SSAFY에서는 1학기에 알고리즘 개념을 전체적으로 다 배운다.
근데 누적합이라는 개념은 들어본 적이 없는듯했다... 그래서 어려운 알고리즘 개념인가 생각하였다..ㅎㅎ
구글링을 하면서 누적합이 뭔지 찾아보았는데 내가 아는 개념이였다..!!
바로 DP에서 1개의 배열로 계속 더해가면서 계산하는 방식이였다. 이 방식을 단순한 DP 문제를 풀때 엄청 많이 적용한 개념이였다.
1번째 커리큘럼이 누적합이기도 하고, 이번에 제대로 개념을 알고 넘어가고자 한다!
🍡 누적합 개념 설명
누적합(Prefix Sum) 알고리즘은 데이터를 효율적으로 처리하기 위해 배열이나 리스트에서 특정 구간의 합을 빠르게 계산하는데 사용되는 알고리즘이다.
이 알고리즘을 통해서 반복 계산의 필요성을 줄이고 성능을 최적화할 수 있다.
또한, 누적합을 통해서 부분합이라는 개념이 나올 수 있다.
부분합은 해당 부분의 합을 구하고 싶을 때, 구한 누적합을 통해서 연산 한번만으로 구할 수 있는 로직이다.
단순한 알고리즘이라서 개념은 이쯤에서 넘어가도 될것 같다.
그리고 사실 나는 이렇게 글로 이해하는 것보다 예제를 보는데 더 이해가 빠른 것 같아서 예제로 바로 넘어가보자!
🍡 누적합의 시간복잡도, 공간복잡도
먼저 1차원과 2차원인 경우를 나눠서 생각해보자!
🎀 1차원 누적합의 문제인 경우
시간복잡도의 경우에는 N개가 들어있는 배열을 한번 순회하니까, O(N)이 된다.
공간복잡도의 경우에도, N의 배열만 사용되기 때문에 O(N)이다.
🎀 2차원 누적합의 문제인 경우
1차원의 경우와는 달리 배열의 크기가 N^2이기 때문에 이것도 한번 순회하므로 , O(N^2)이 된다.
공간복잡도도 동일하게, 2차원 배열만 그대로 사용되기 때문에 O(N^2)이다.
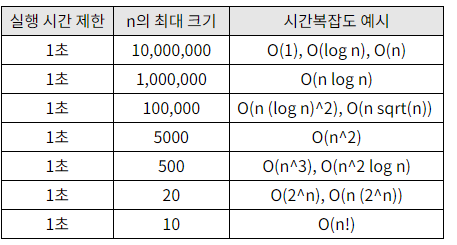
시간복잡도별 실행시간에 따른 n의 크기이다.
따라서, 1차원의 경우에는 N이 10,000,000까지 가능하고, 2차원은 N이 5000까지일때 누적합을 사용할 수 있다.
항상 문제의 알고리즘을 적용할 때 시간복잡도를 보는 습관을 가져야 한다!!
🐤 누적합 예제
🍡 누적합 예제 1 ) 수열(2559)
https://www.acmicpc.net/problem/2559
먼저, 백준의 기본 누적합 문제인 수열(2559)에 대해 풀어보자.
이 문제의 시간복잡도를 먼저 살펴보자!
여기서 N은 2이상 100,000 이하이므로 천만보다 작기 때문에 누적합으로 풀이가 가능하다!
그리고 이 문제는 연속적인 며칠 동안 온도의 합이 가장 큰 값을 구하는 것이므로, 누적합을 통해서 최종적으로 부분합을 구하는 문제이다.
문제의 예시를 통해 정확히 풀어보자!
-
10일간의 온도가 주어졌다.

-
부분의 합을 알기 위해 누적합을 구해보자
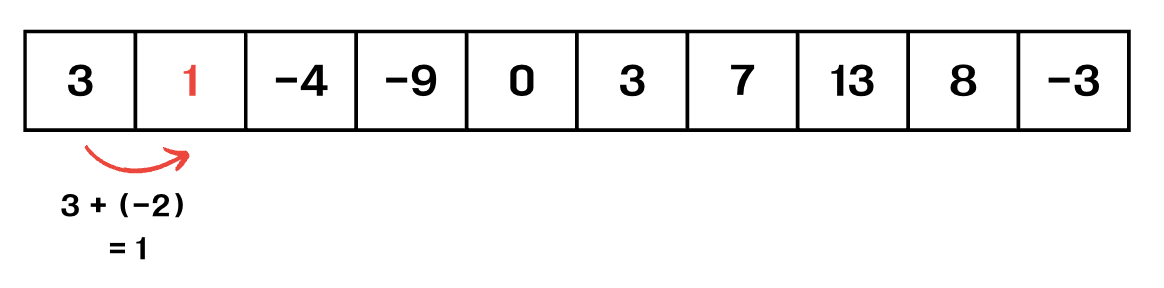
2-1. 이전의 누적합에서 자신을 더한것을 해당 배열에 저장한다.
1번째 값이 3이고 2번째 값이 -2이기때문에 3+(-2) = 1로 배열에 저장한다.
이런식으로 배열을 반복하면서 해당 배열의 누적합을 저장한다!
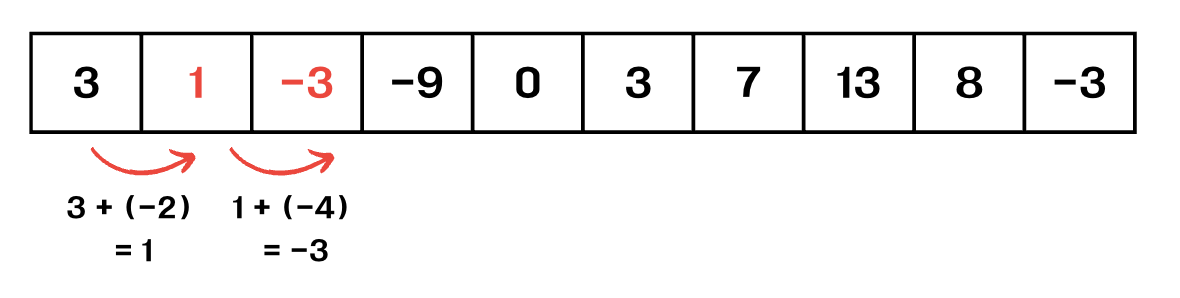

여기서 코드로 구현시, 중요한 점이 있다.
1번째 인덱스의 값을 배열 0에서부터 시작할 경우, 0번은 -1이 없기 때문에 추가적인 조건문을 써야한다.
이러한 것을 줄이기 위해, 임의적으로 0번의 인덱스에는 0을 넣고, 1번부터 시작해서 arr[N+1] 배열을 만들자!!
🎀 1차원 누적합 구현 코드
밑의 코드와 같이 배열의 크기를 N+1만큼하고, 반복문을 통해 arr[i]에 자신의 값과 i-1까지의 누적합을 더해서 저장한다.
int[] arr = new int[N+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=N;i++){
arr[i] = Integer.parseInt(st.nextToken()) + arr[i-1];
}- 이제 누적합을 모두 구했다면, 진짜 답인 부분합을 구해야 한다.
이 예시에서 해당 부분의 크기는 K라는 것으로 정해져 있고 우리는 K가 2라고 가정해보자.
3-1. 부분합을 구하려면, (부분의 마지막 인덱스의 누적합) - (부분의 마지막 인덱스 - K의 누적합) 이렇게 구현하면 해당 부분의 합이 도출된다.
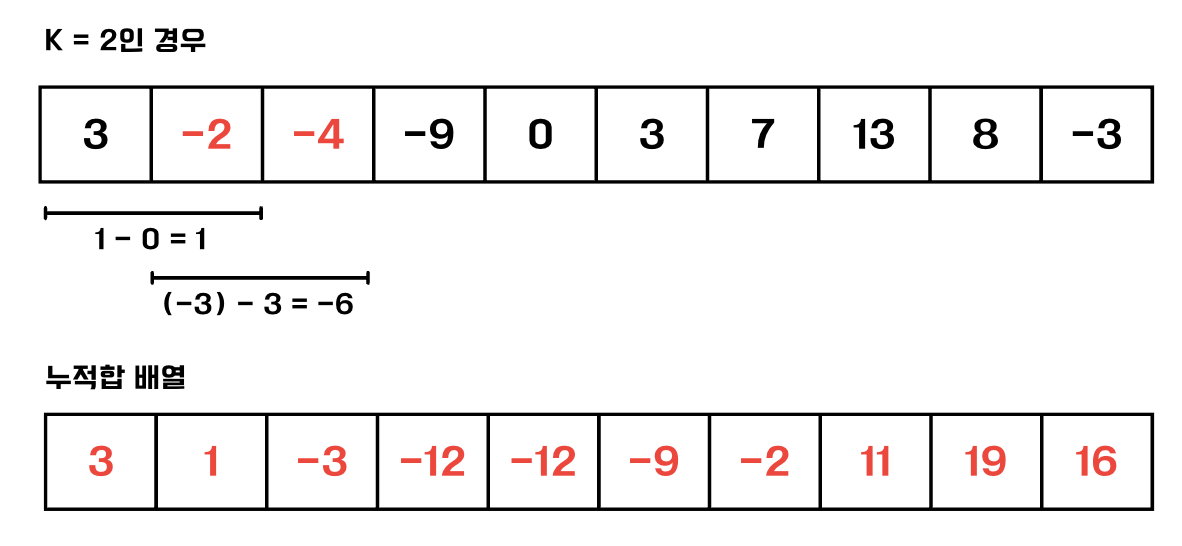
🎀 1차원 부분합 구현 코드
for문을 사용해 K~N까지 돌리면서, 누적합 배열인 arr로 (arr[i] - arr[i-K]) 의 최대값을 찾는다.
K부터 시작하는 이유는 1부터 K까지는 앞에 뺄 값이 없기 때문에 누적합 그대로이기도 하고, -K를 할때 인덱스가 0보다 작아질 경우를 대비해서이다.
answer = arr[K];
for(int i=K;i<=N;i++){
answer = Math.max(answer,arr[i]-arr[i-K]);
}🎀 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Bj_2559_수열 {
public static void main(String[] args) throws IOException{
BufferedReader br =new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int answer =0;
int[] arr = new int[N+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=N;i++){
arr[i] = Integer.parseInt(st.nextToken()) + arr[i-1];
}
answer = arr[K];
for(int i=K;i<=N;i++){
answer = Math.max(answer,arr[i]-arr[i-K]);
}
System.out.println(answer);
}
}
🎀 회고
이렇게 부분합의 1차원배열 기본 문제를 풀어보았다.
백준 Java8기준 19등으로 1페이지안에 들어서 기분이 좋았다 ㅎㅎ

🍡 누적합 예제 2 ) 구간 합 구하기 4(11659)
https://www.acmicpc.net/problem/11659
이 문제는 위의 수열 문제와 푸는 방법은 동일한데, 부분합에서 구해야하는 부분을 입력받기 때문에 이 점만 다르다고할 수 있다.
- 일단 중요한것 첫번째 문제를 풀기 전에 시간복잡도를 먼저 보자
- N이 10만이고, 시간 제한은 1초이므로 누적합 O(N)의 N은 천만까지이므로 풀이가 가능하다.
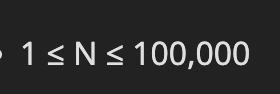
- 위의 문제와 동일하게 누적합을 먼저 구하자
-
예제 입력 1의 예시

-
누적합을 구하면 이렇게 배열이 완성된다.

🎀 1차원 누적합 구현 코드
int[] arr = new int[N+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=N;i++) {
arr[i] = Integer.parseInt(st.nextToken()) + arr[i-1];
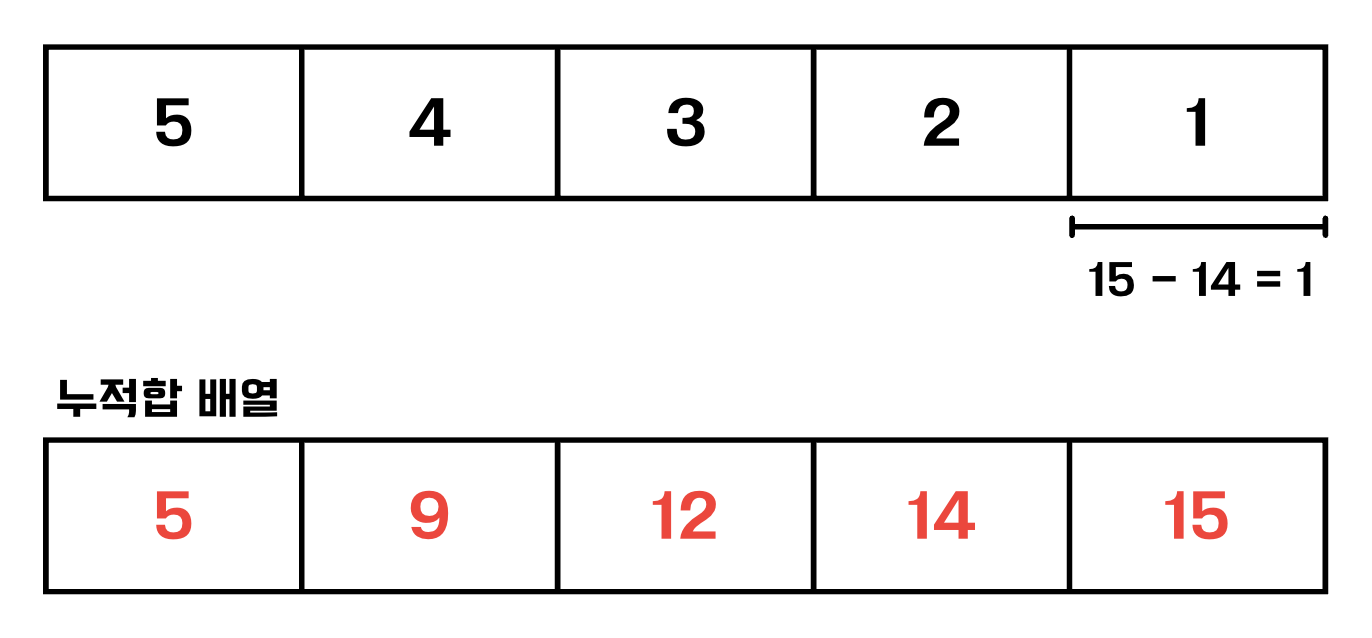
}- 이제 입력 값들에 따라 부분합을 구해보자
- 공식으로는 arr[j] - arr[i-1] 를 해주면 된다.
3-1. 1번째 구간은 i=1 ~ j=3
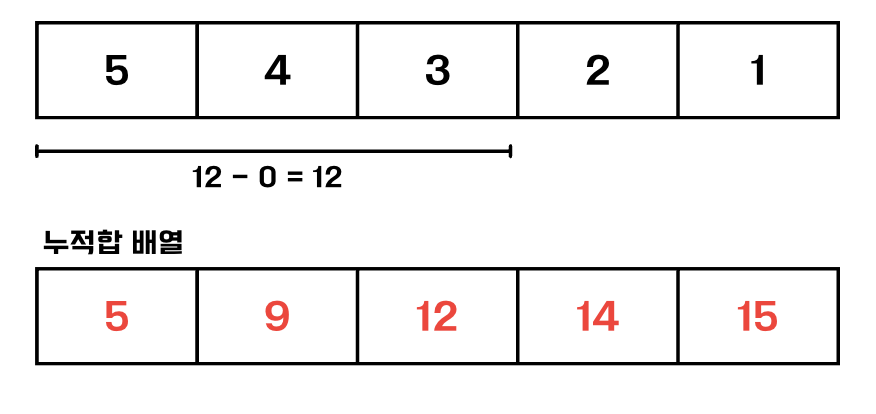
3-2. 2번째 구간은 i=2 ~ j=4
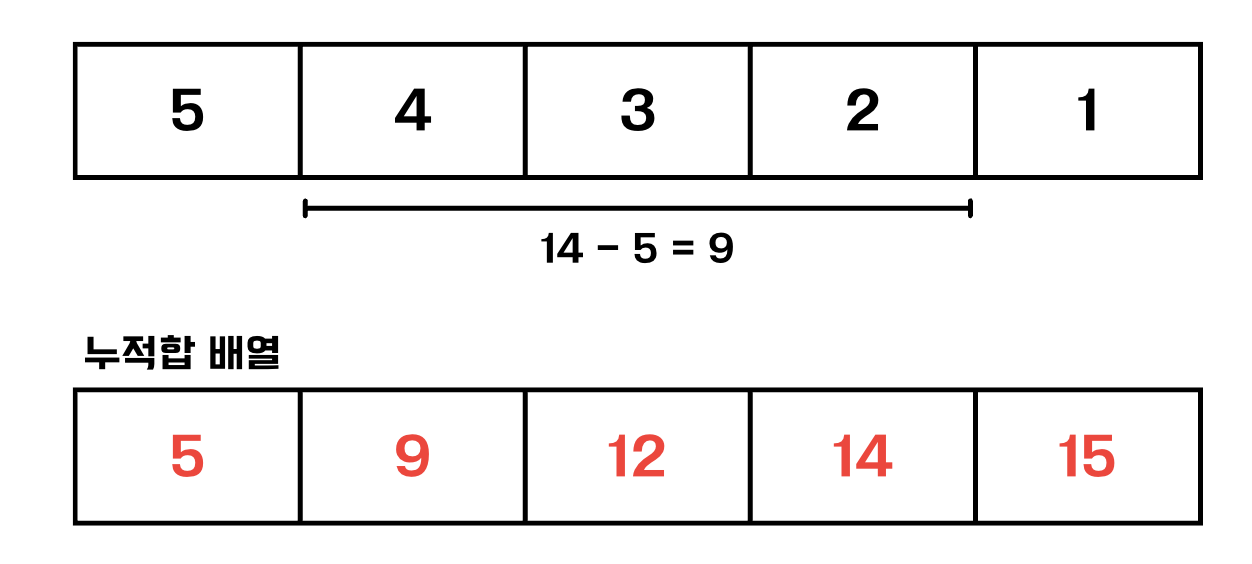
3-3. 3번째 구간은 i=5 ~ j=5
🎀 1차원 부분합 구현 코드
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
sb.append(arr[end]-arr[start-1]).append("\n");
}🎀 전체 코드
import java.util.StringTokenizer;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Bj_11659_구간합구하기4 {
public static void main(String[] args)throws Exception{
BufferedReader br =new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] arr = new int[N+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=N;i++) {
arr[i] = Integer.parseInt(st.nextToken()) + arr[i-1];
}
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
sb.append(arr[end]-arr[start-1]).append("\n");
}
System.out.println(sb.toString());
}
}🎀 회고
이렇게 부분합의 1차원배열 문제를 풀어보았다.
이제 조금 부분합에 대해서 알 것 같다!
백준 Java8기준 27등을 했다.

🍡 누적합 예제 3 ) 구간 합 구하기 5(11660)
https://www.acmicpc.net/problem/11660
이 문제는 2차원 누적합 문제이다.
2차원이기 때문에, 시간복잡도에 대해서 꼭 확인해봐야 한다!
-
시간복잡도 체크
NxN 배열이라서 시간복잡도가 O(N^2)이고 1초에 5000까지 가능하다.
이 문제에서는 N이 1024까지이므로 누적합으로 푸는 것이 가능하다!
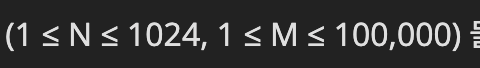
-
시간복잡도를 확인했으면 2차원 누적합을 구해보자
-
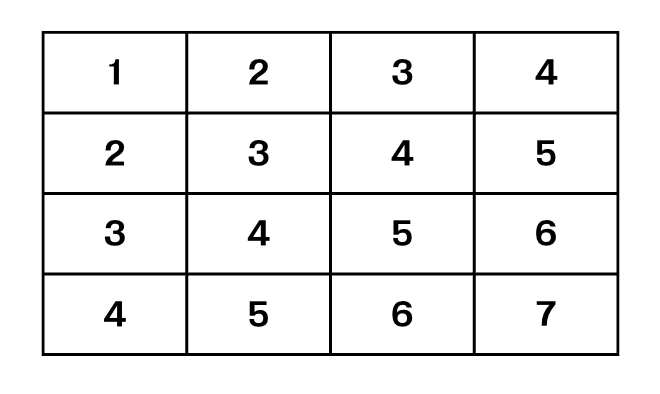
문제의 예시처럼 N=4인 경우
-
2차 for문으로 (1,1)부터 해당 값인 (i,j)까지의 누적합을 저장한다.
2차원 누적합을 구할 때는,1차원 누적합 배열과는 달리 겹치는 부분이 생기기 때문에 이걸로 고려해서 겹치는 부분은 빼고 계산해야한다!
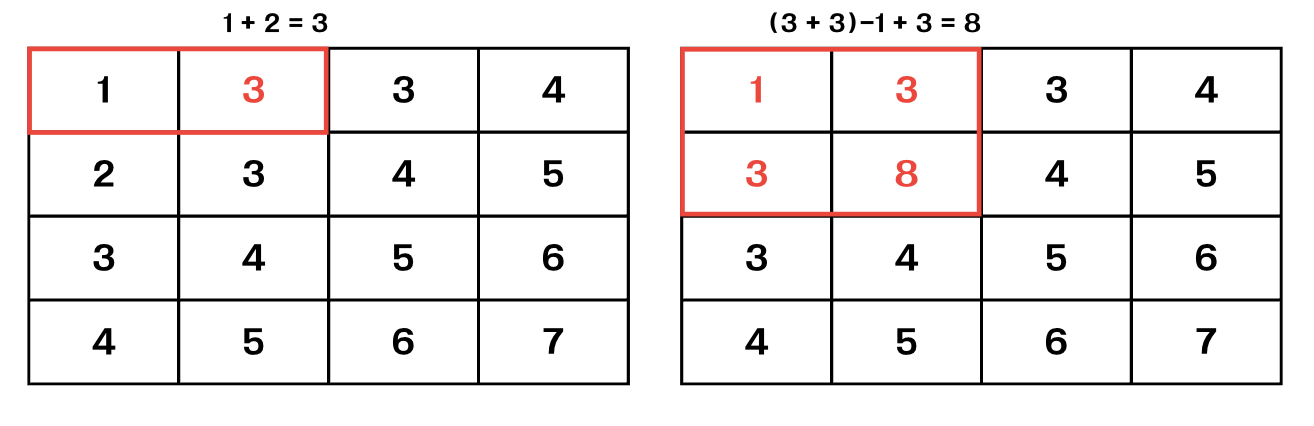
공식 : arr[i-1][j]+arr[i][j-1] - arr[i-1][j-1]) + arr[i][j]
여기서 arr[i-1][j-1] 이부분이 바로 겹치는 부분이다!
🎀 2차원 누적합 구현 코드
2차원 누적합도 동일하게 조건문이 추가되지 않기 위해 배열을 [N+1][N+1]로 잡아서 i-1이나 j-1을 했을때 오류를 막을 수 있다.
arr =new int[N+1][N+1];
for(int i=1;i<=N;i++){
st = new StringTokenizer(br.readLine());
for(int j=1;j<=N;j++){
arr[i][j] = Integer.parseInt(st.nextToken())+(arr[i-1][j] + arr[i][j-1] -arr[i-1][j-1]);
}
}- 이제 정답인 입력값들에 대한 2차원의 부분합을 구해보자
- 입력 값을 x1,y1,x2,y2라고 한다면 arr[x2][y2]의 누적합에서 빼야하는 부분인 arr[x2][y1-1]과 arr[x1-1][y2]를 빼주고 중복으로 들어간 값인 arr[x1-1][y1-1]을 한번 더해주면 된다.
공식 : arr[x2][y2] - arr[x2][y1-1] - arr[x1-1][y2] + arr[x1-1][y1-1]
3-1. 1번째 구간은 (2,2) ~ (3,4)
3-2. 2번째 구간은 (3,4) ~ (3,4)
3-3. 3번째 구간은 (1,1) ~ (4,4)
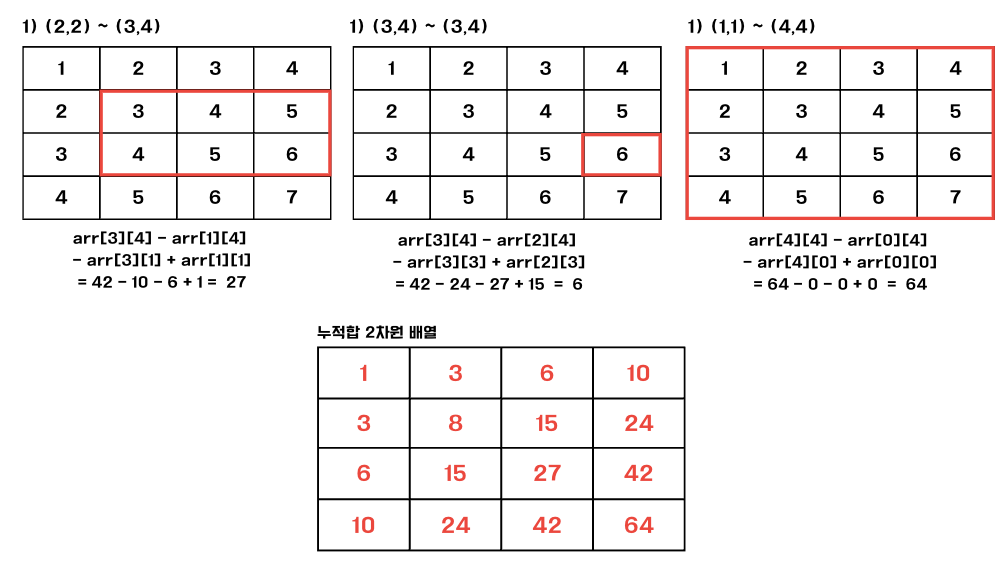
🎀 2차원 부분합 구현 코드
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
calculate(x1,y1,x2,y2);
}
static void calculate(int x1,int y1,int x2, int y2){
int result = arr[x2][y2]-arr[x2][y1-1]-arr[x1-1][y2]+arr[x1-1][y1-1];
}🎀 전체 코드
import java.util.*;
import java.io.*;
public class Bj_11660_구간합구하기5 {
static int N,M;
static StringBuilder sb = new StringBuilder();
static int[][] arr;
public static void main(String[] args) throws Exception{
BufferedReader br =new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st =new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr =new int[N+1][N+1];
for(int i=1;i<=N;i++){
st = new StringTokenizer(br.readLine());
for(int j=1;j<=N;j++){
arr[i][j] = Integer.parseInt(st.nextToken())+(arr[i-1][j] + arr[i][j-1] -arr[i-1][j-1]);
}
}
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
calculate(x1,y1,x2,y2);
}
System.out.println(sb);
}
static void calculate(int x1,int y1,int x2, int y2){
int result = arr[x2][y2]-arr[x2][y1-1]-arr[x1-1][y2]+arr[x1-1][y1-1];
sb.append(result).append("\n");
}
}
🎀 회고
2차원의 누적합과 부분합에 대해서 이해가 완료된것 같다.
더 심화된 누적합 문제를 찾아서 풀어보면 좋을 것 같다!!!
🐤 마무리
이렇게 누적합의 개념을 공부하고 3개의 문제를 풀어 봤는데 문제를 풀고 복습의 느낌으로 블로그를 정리하면 훨씬 기억에 더 잘남는것 같다!!
앞으로도 알고리즘 개념을 먼저 공부하고, 여러개의 문제를 풀고 블로그에 정리하면서 복습하는 형식으로 하면 좋을 것같다.
취준이 힘들긴 하겠지만, 열심히 하면 그만큼 성과가 따를것이라고 확신한다!!
그러니까 매일 내일만 보고 열심히 그냥 하자!
다음 블로그는 누적합의 확장인 IMOS로 돌아오겠습니다~