Digital System

Digital circuit = Logic circuit

Digital System

discrete or seperate over time

Analog System

continuous over time

---

3-1 Boolean Constants and Variables

Boolean algebra allows only two values → 0 and 1

Logic 0	Logic 1
False	True
Off	On
LOW	HIGH
No	Yes
Open switch	Closed switch

---

3-2 Truth Tables

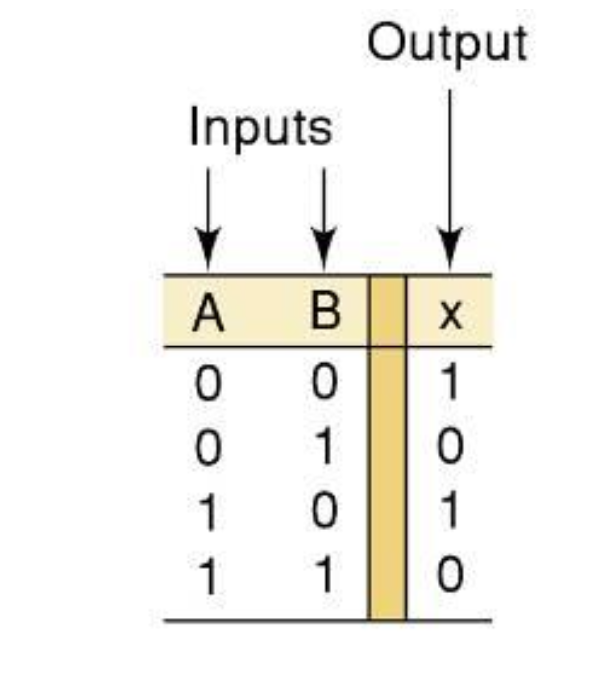
A truth table describes the relationship between the input and output of a logic circuit.

The number of entries corresponds to the number of inputs.

• A 2-input table would have 2^2 = 4 entries.
• A 3-input table would have 2^3 = 8 entries.

---

3-3 OR Operation With OR Gates

+ = "OR"

1 + 1 = 1

→ OR은 하나라도 1이면 결과가 1인 연산이다.

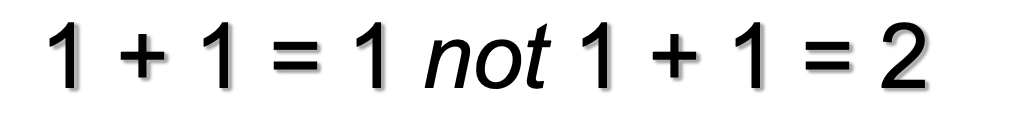
OR Gate

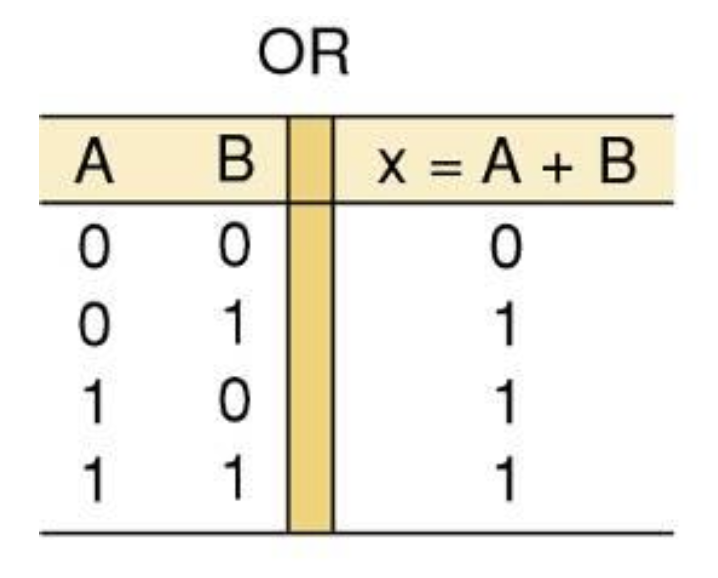
OR Gate is a circuit(Logic Circuit) with two or more inputs, whose output is equal to the OR combination of the inputs

OR Truth table

Two input OR Gate Symbol

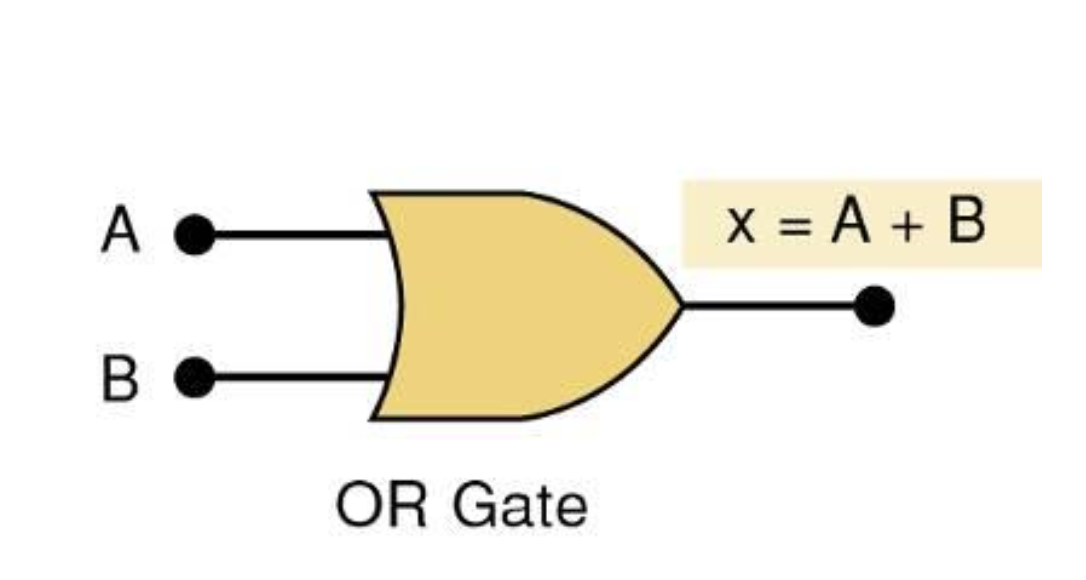
two input → all possible cases = 4

Three input OR Gate Symbol

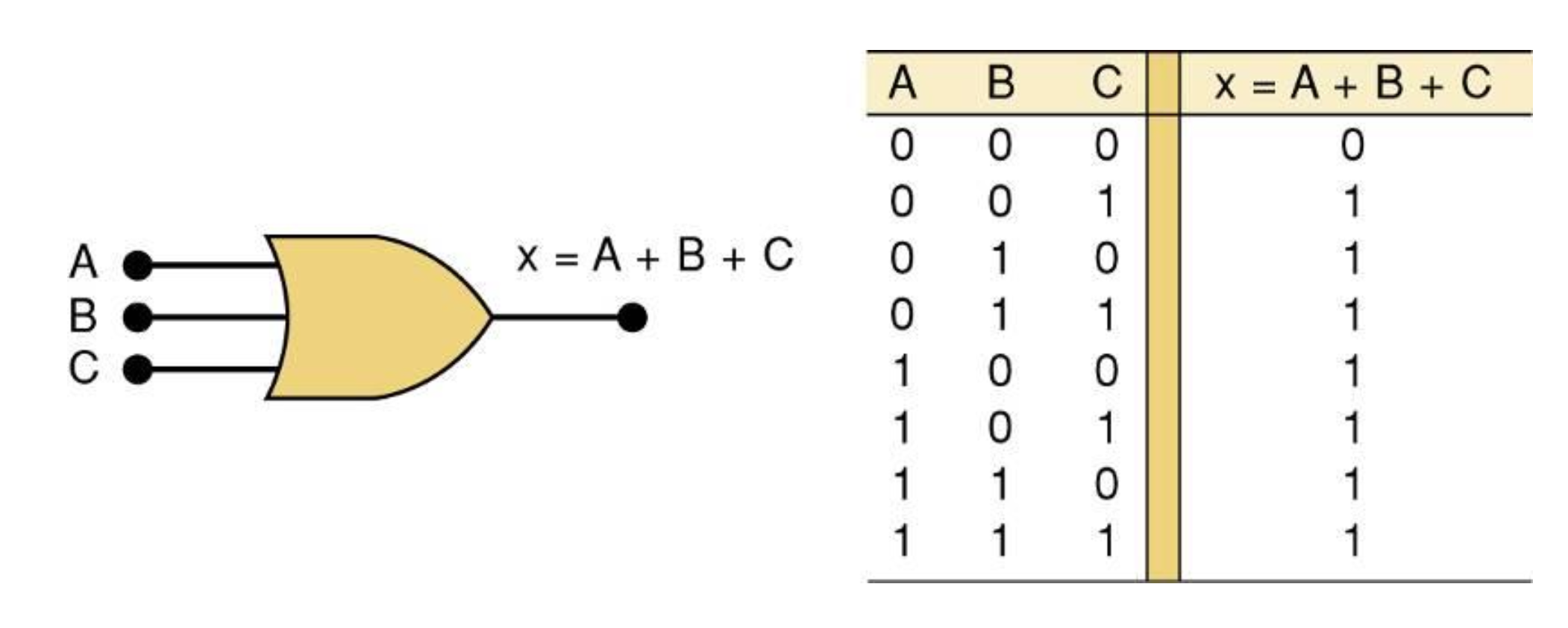
not popular

---

3-4 AND Operations with AND Gates

* = "AND"

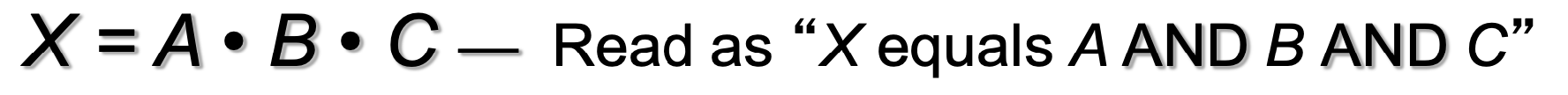
→ 전부 1일(true) 때만 결과가 1이 나온다.

AND Truth table

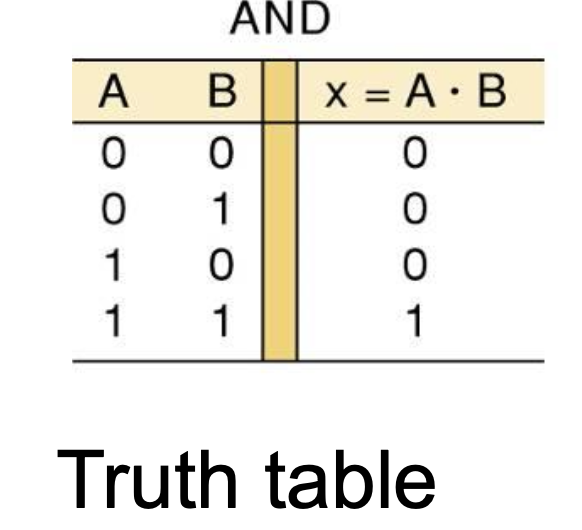
AND Gate Symbol

---

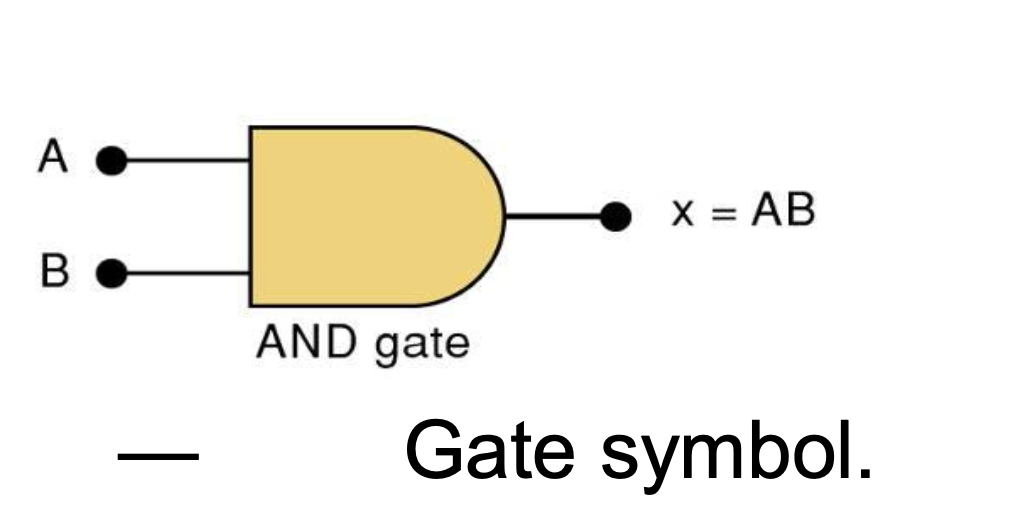
3-5 NOT Operation

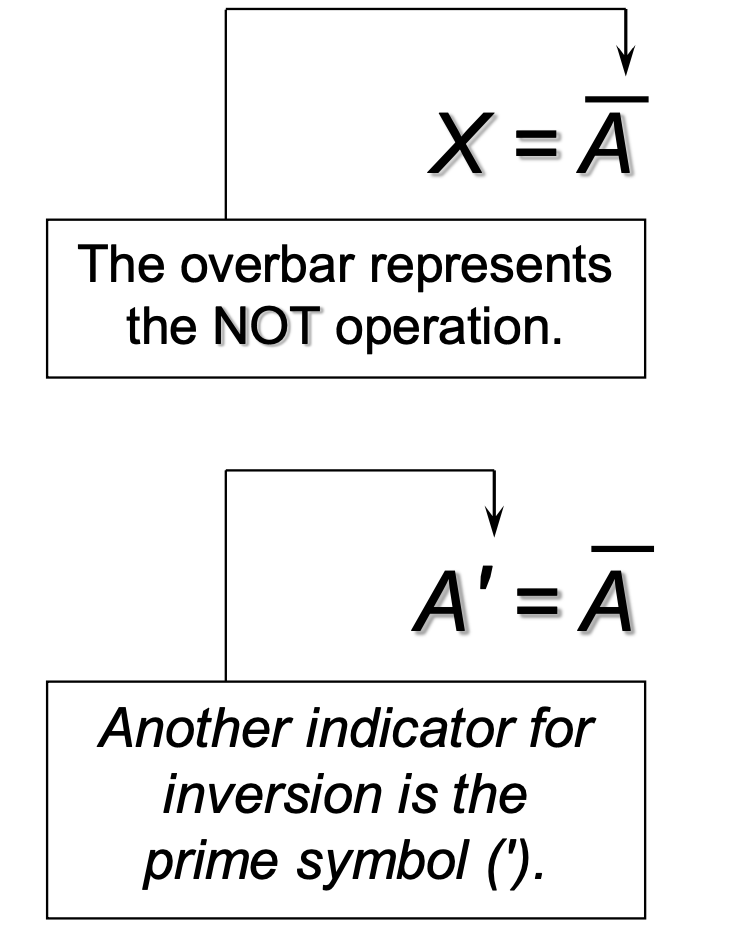
NOT A

= Bar A
= inverse of A
= complement(여집합) of A

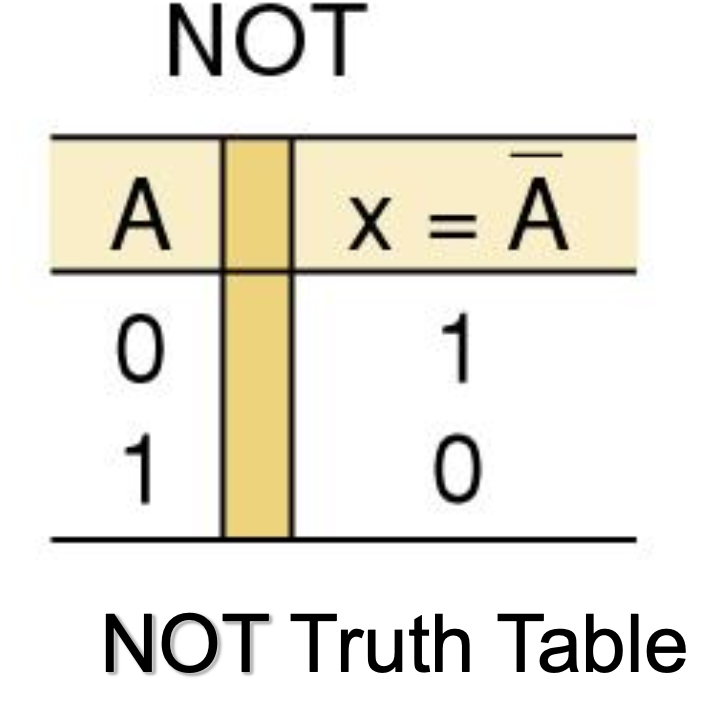
NOT Truth Table

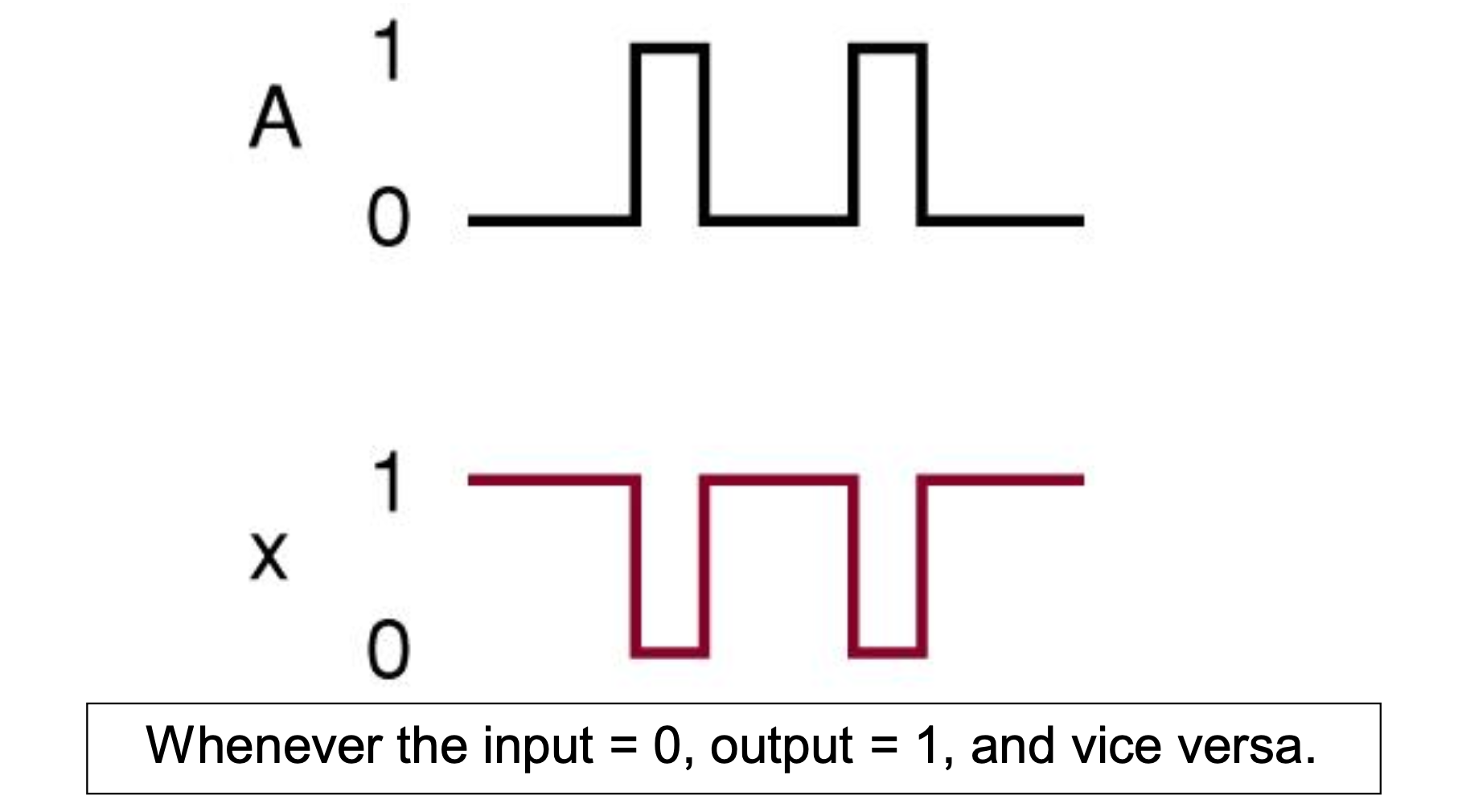
NOT Symbol

1 input → 1 output

INVERTER

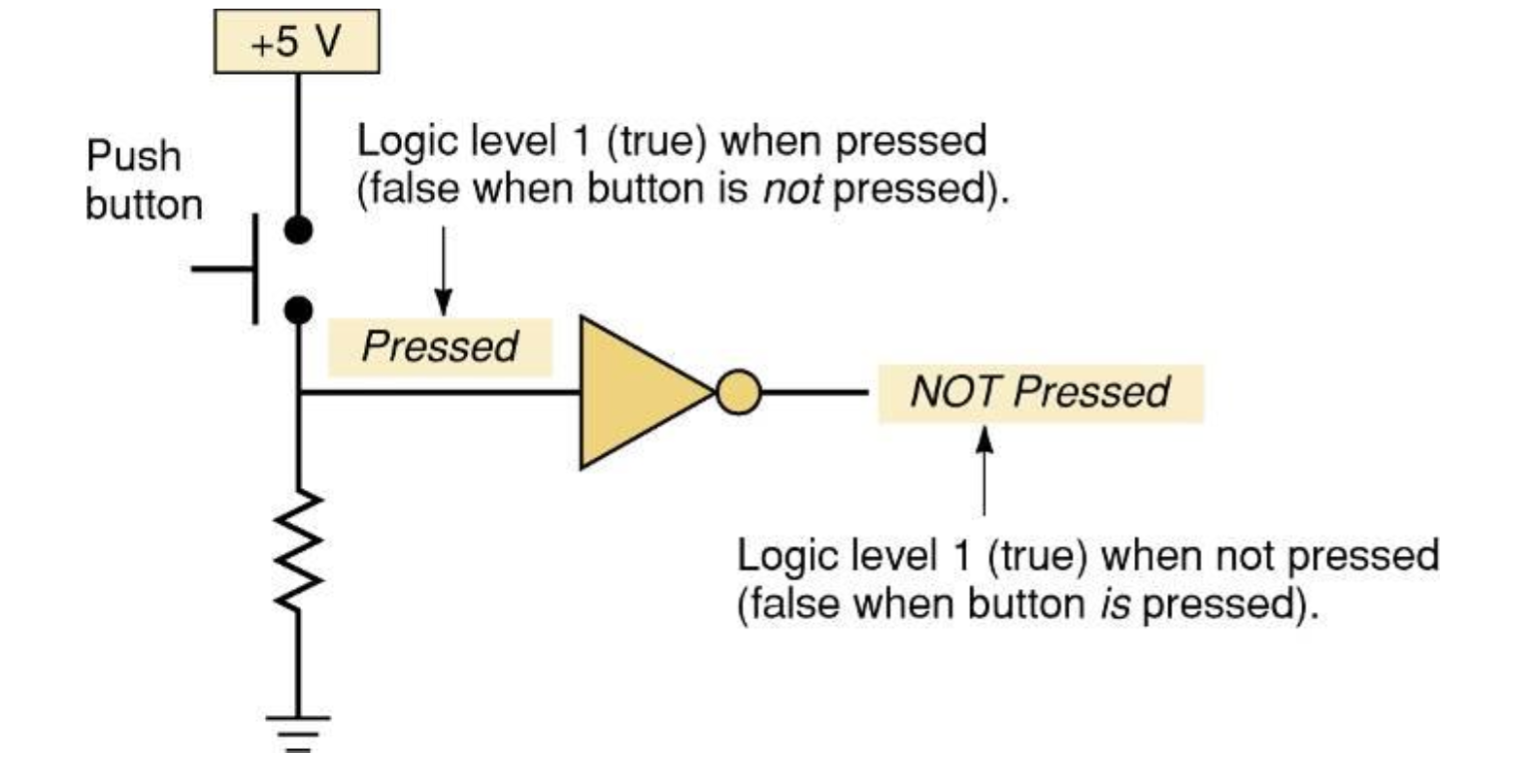
전형적인 NOT Gate

스위치가 눌리지 않은 상태 → 0 → NOT Gate → 1 = NOT Pressed

---

3-6 Describing Logic Circuit Algebraically

---

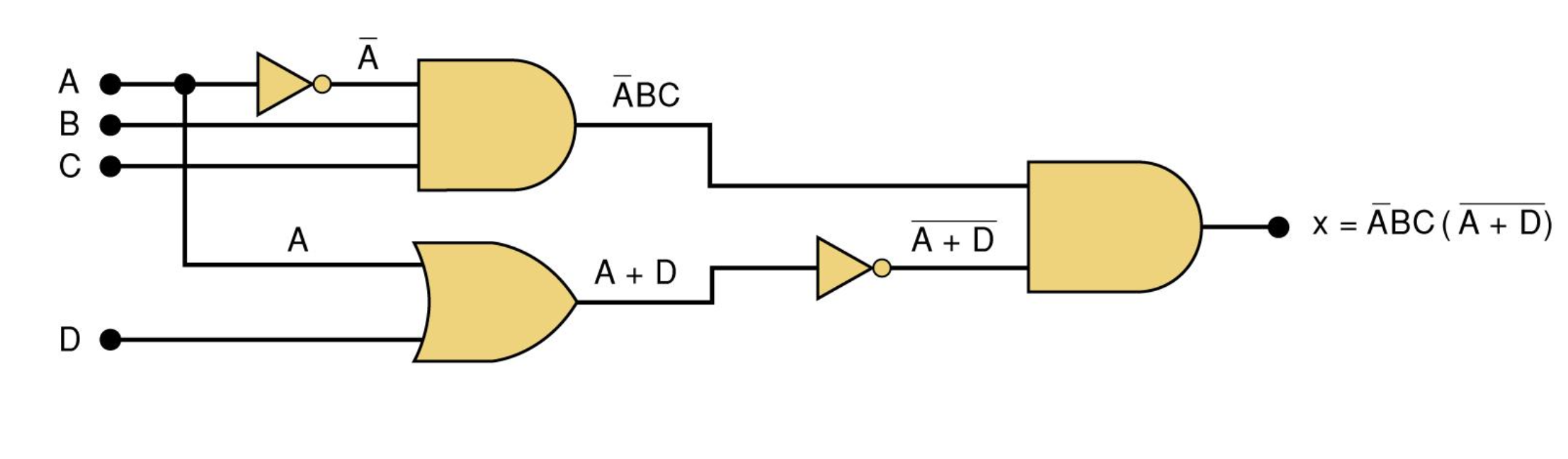
3-7 Evaluating Logic Circuit Outputs

Step 1

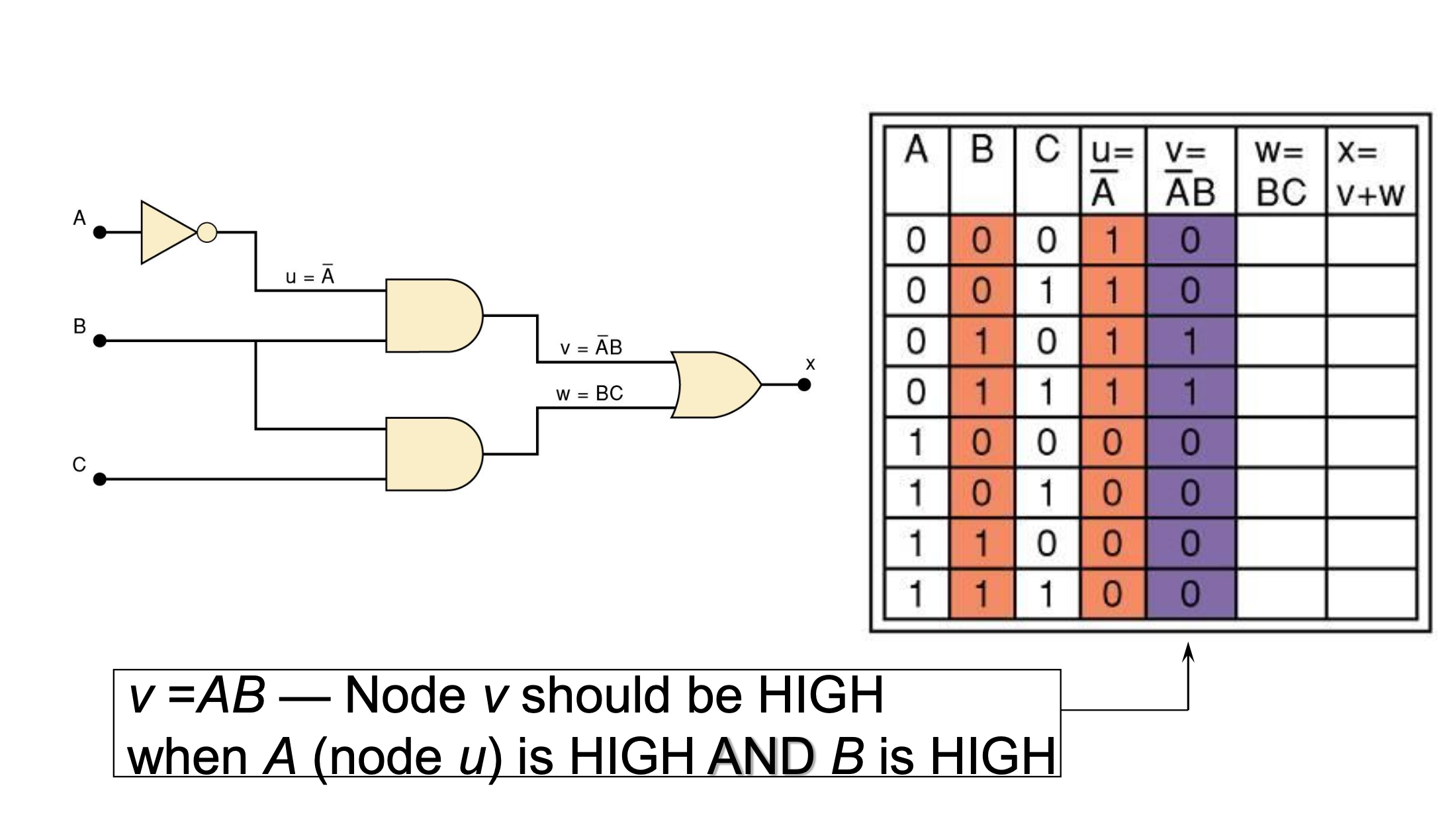
Step 2

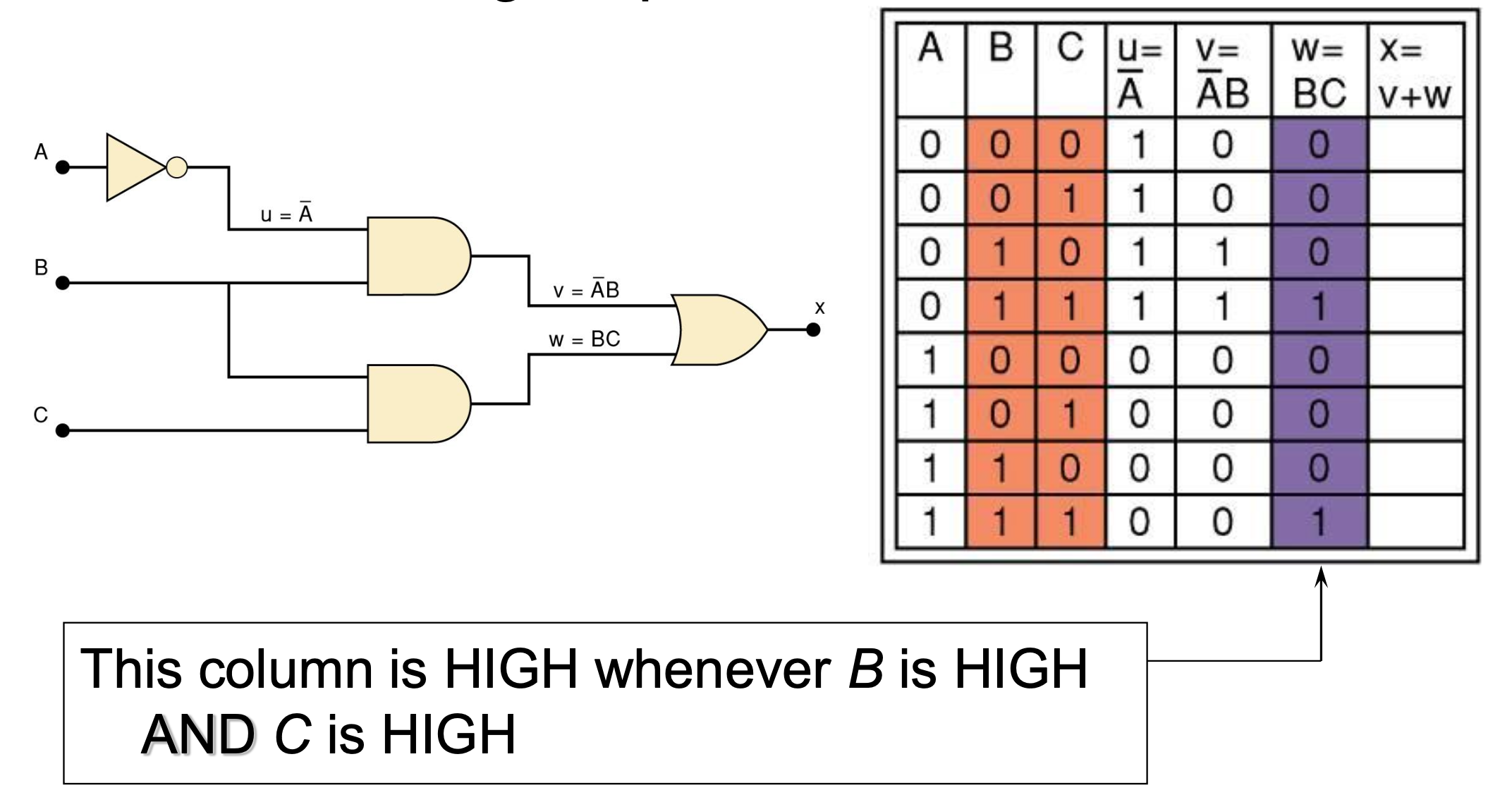
Step 3

---

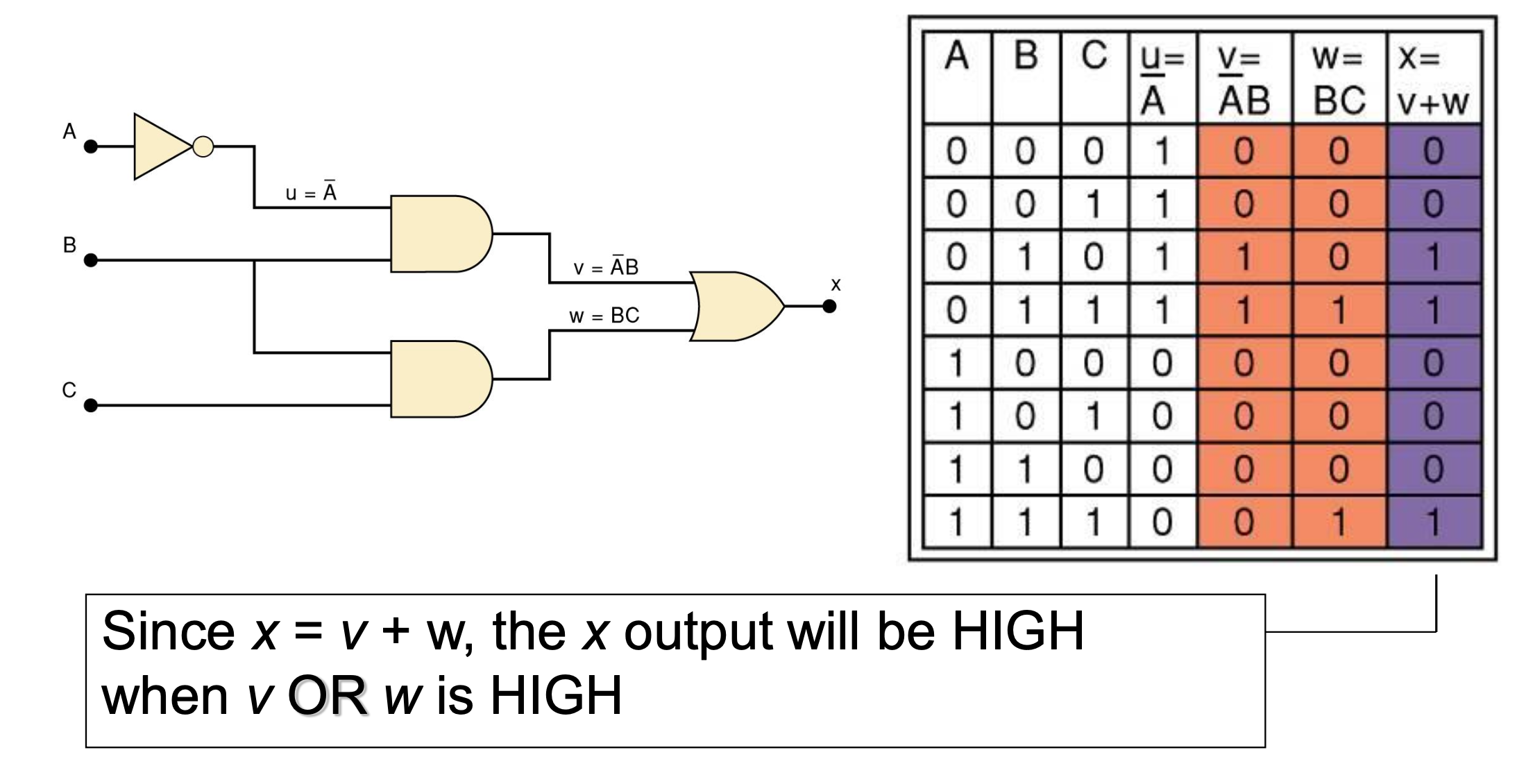
3-9 NOR Gates and NAND Gates

NOR Gate

OR 하고 NOT 하는 로직을 합친 게이트

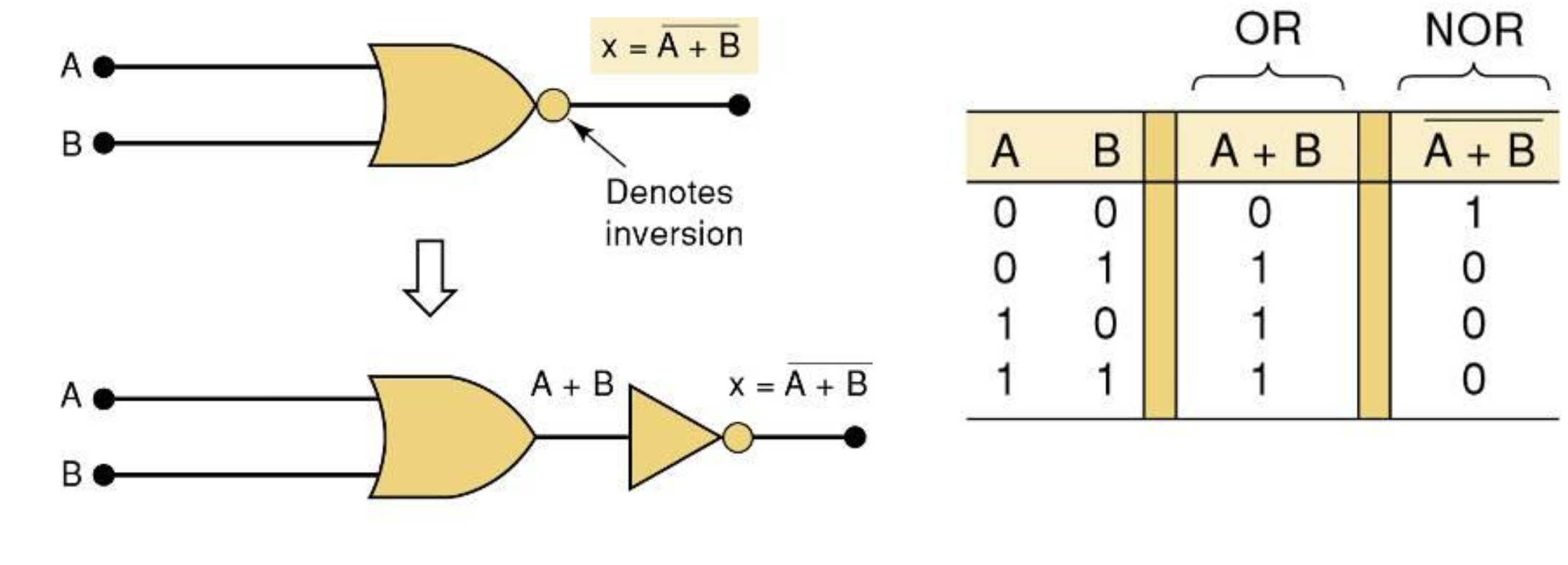
NAND Gate

AND 하고 NOT 하는 로직을 합친 게이트

---

3-10 Boolean Theorems

AND

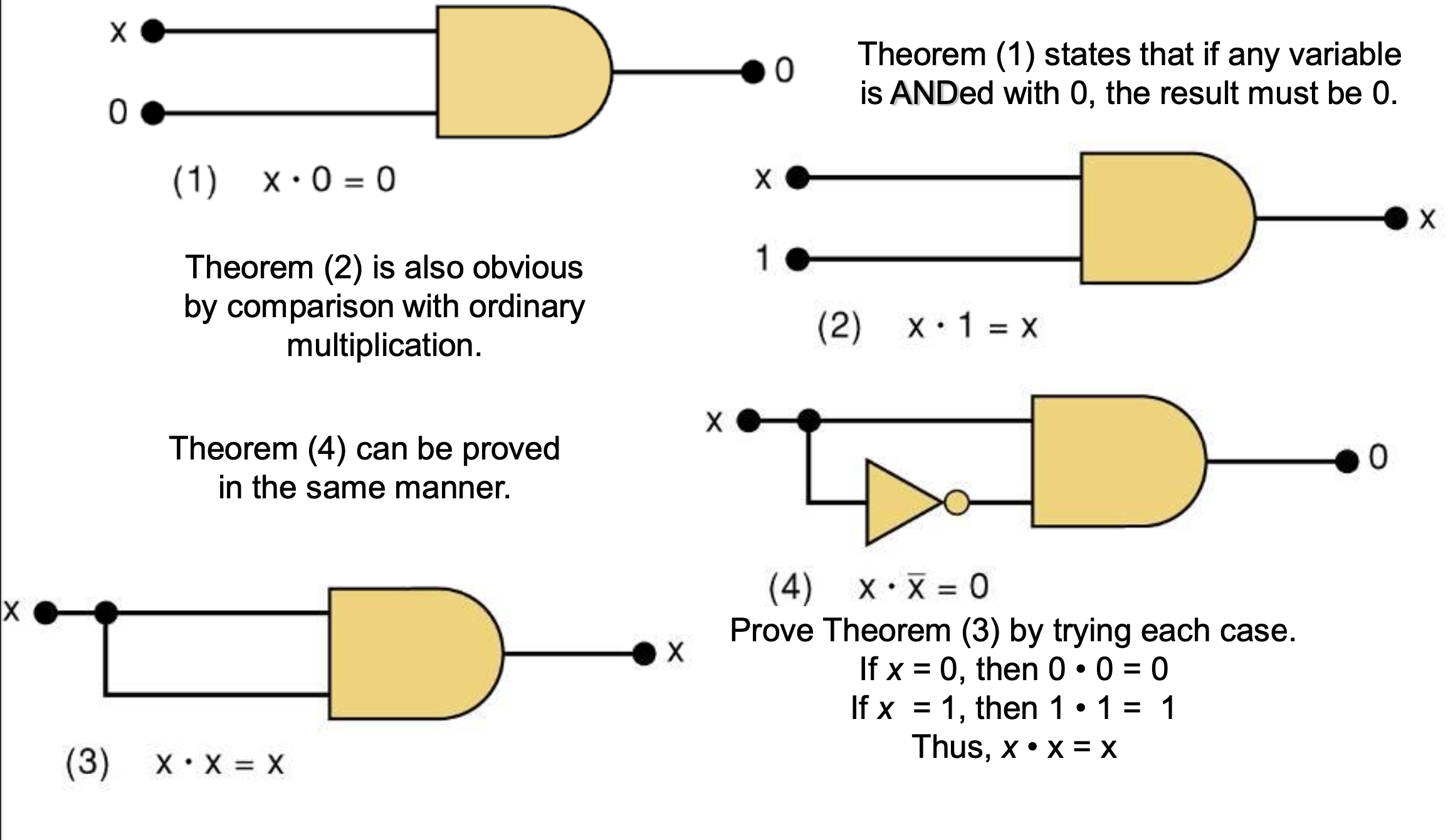
1. X*0 = 0

2. X*1 = X

3. X*X = X

4. X*!X = 0

OR

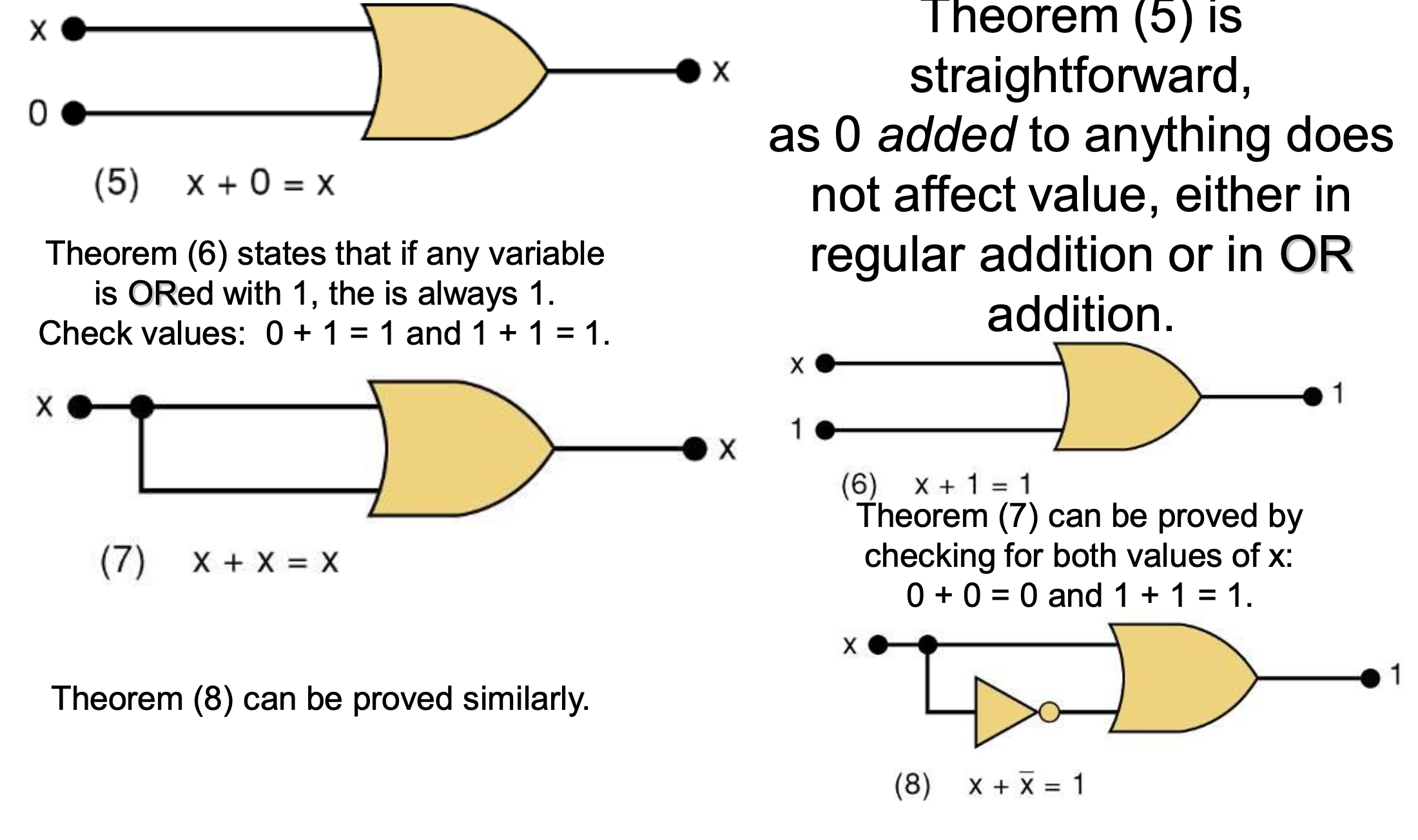
5. X + 0 = X

6. X + 1 = 1

7. X + X = X

8. X + !X = 1

Commutative laws
(교환법칙)

9. X + Y = Y + X

10. XY = YX

Associative laws
(결합법칙)

11. X + (Y + Z) = (X + Y) + Z = X + Y + Z

12. X(YZ) = (XY)Z = XYZ

Distributive law
(분배법칙)

13a. X(Y + Z) = XY + XZ

13b. (W + X)(Y + Z) = WY + XY + WZ + XZ

14. X + XY = X

X(1 + Y) = X*1 = X

15a. X + !XY = X + Y

15B. !X + XY = !X + Y

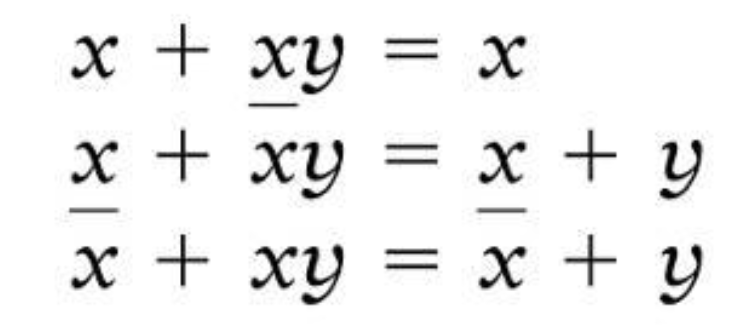
	input	output
x+y	high	high

---

3-11 DeMorgan's Theorems

16. !(X + Y) = !X*!Y

17. !(X*Y) = !X + !Y

---

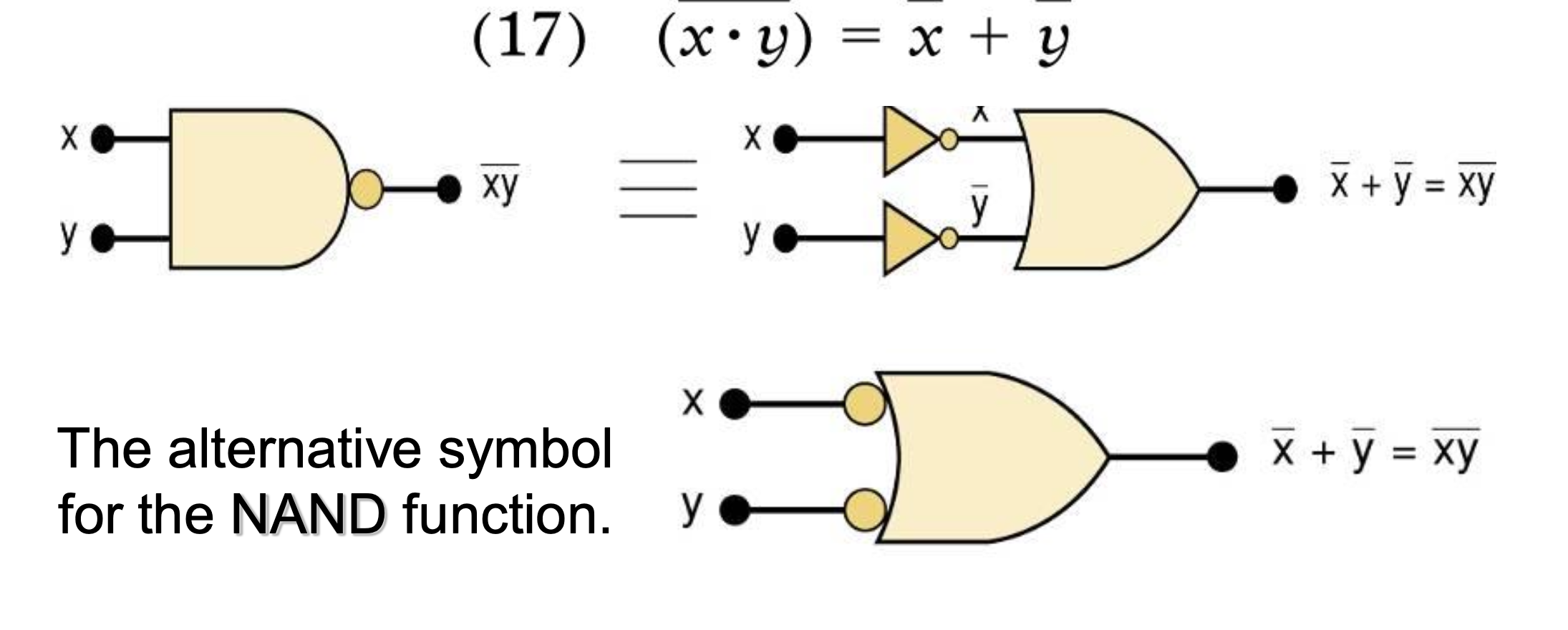
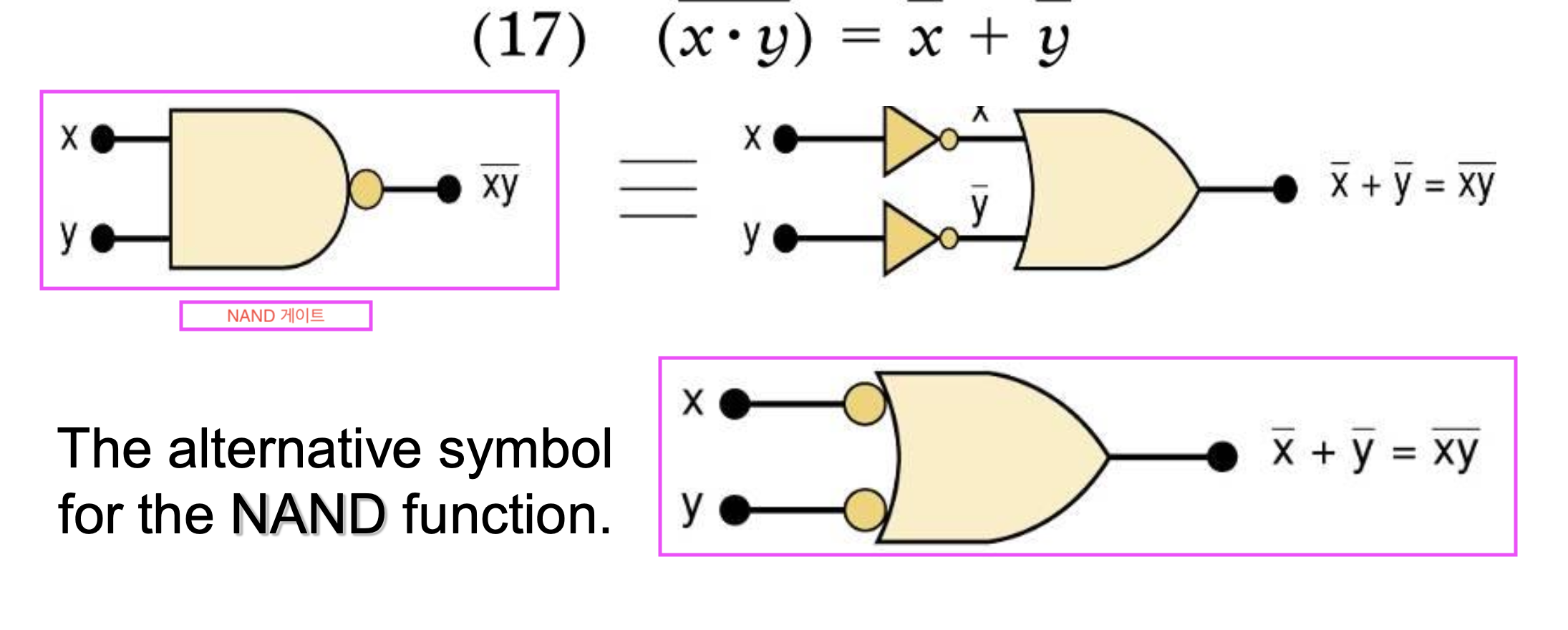
두 게이트는 서로 생김새가 다르지만, 결과값은 동일하다.
단, 관점이 다르다.

• 왼쪽 게이트: 언제 0이 되지?
• 오른쪽 게이트: 언제 1(high)가 되지?

---

3-12 Universality of NAND and NOR Gates

Basic three gate
→ OR, AND, NOT(INVERT)

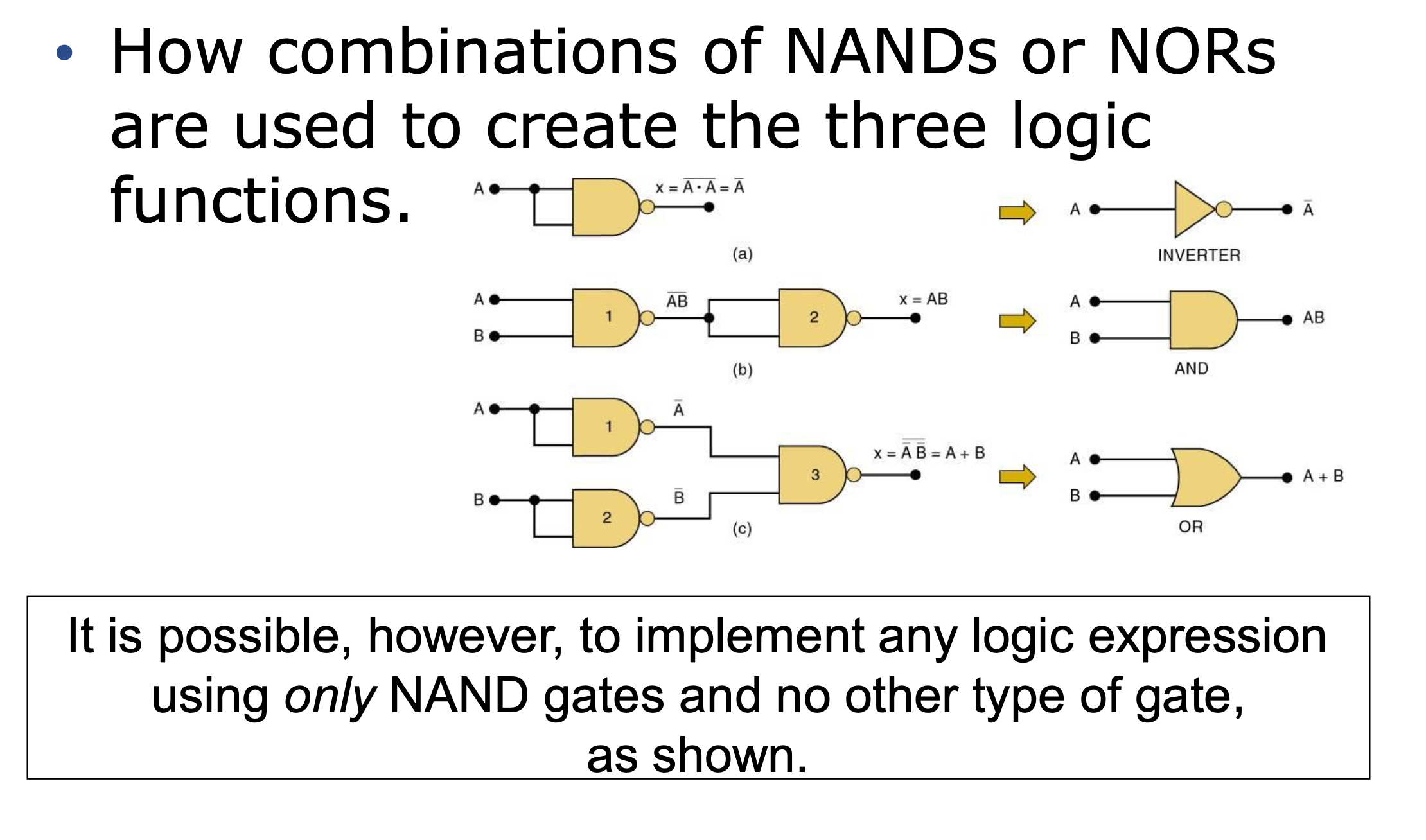
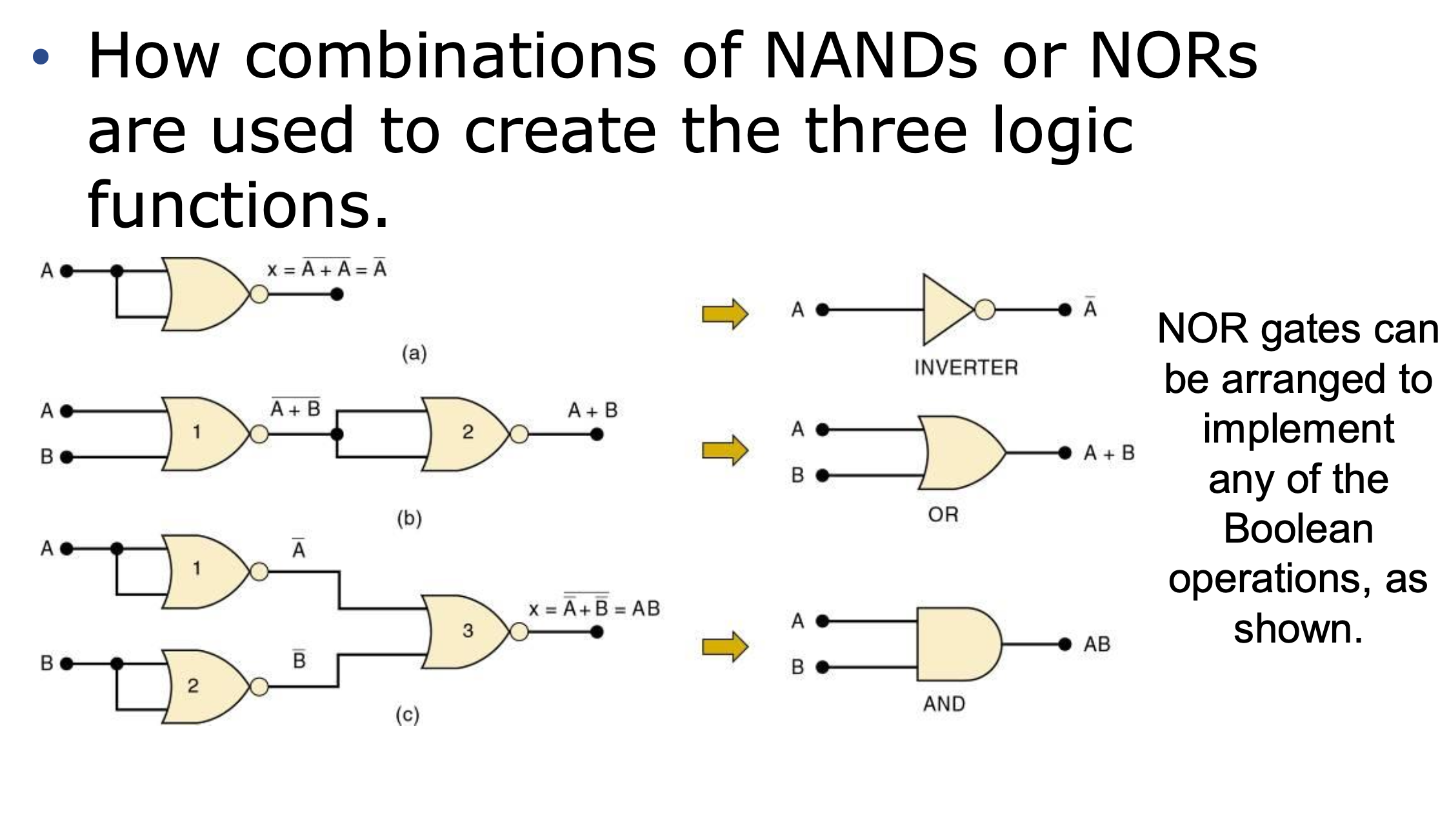
조건이 뭐든간에 항상 결과가 HIGH인 logic circuit

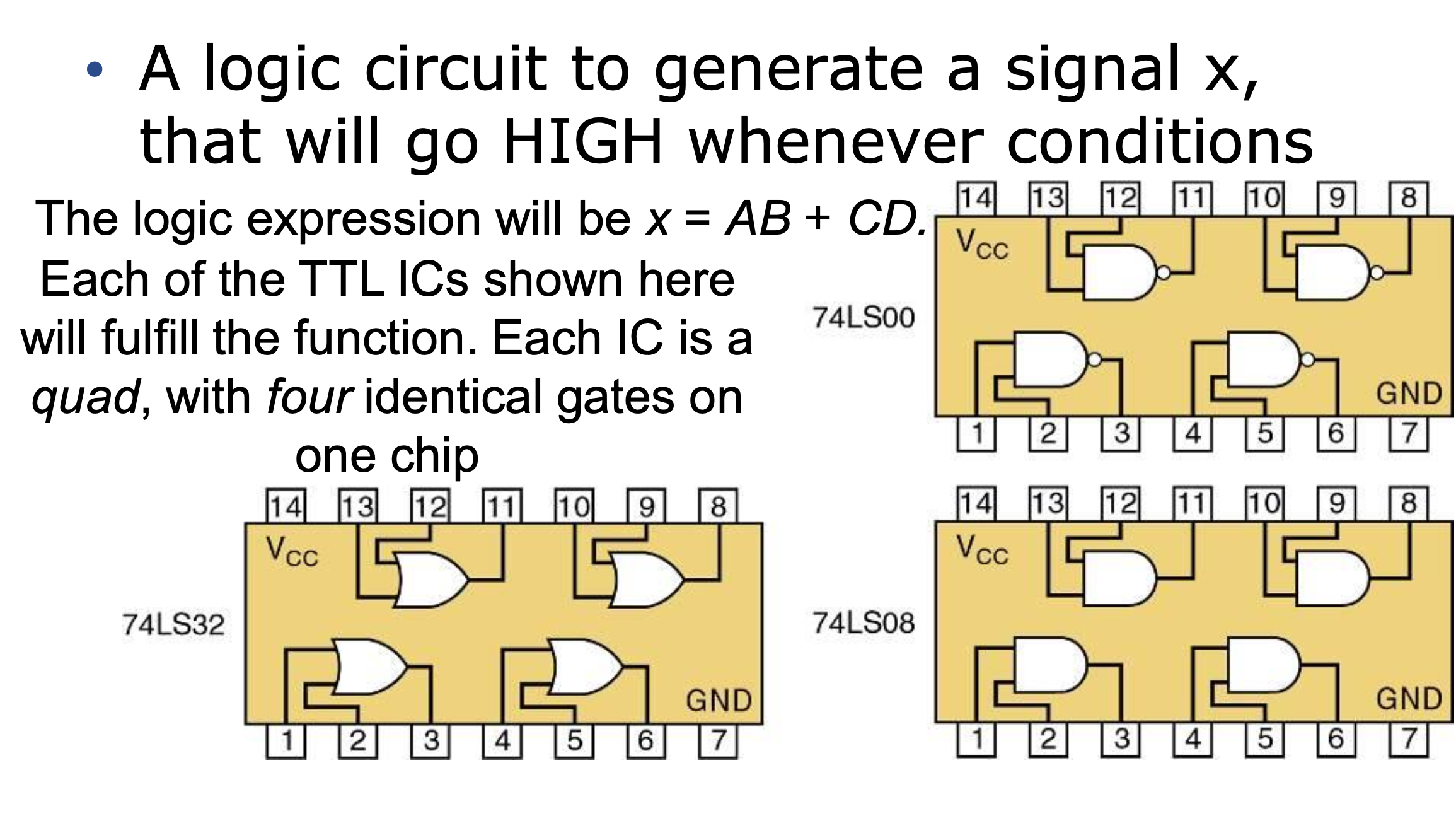
Possible Implementations # 1 ??

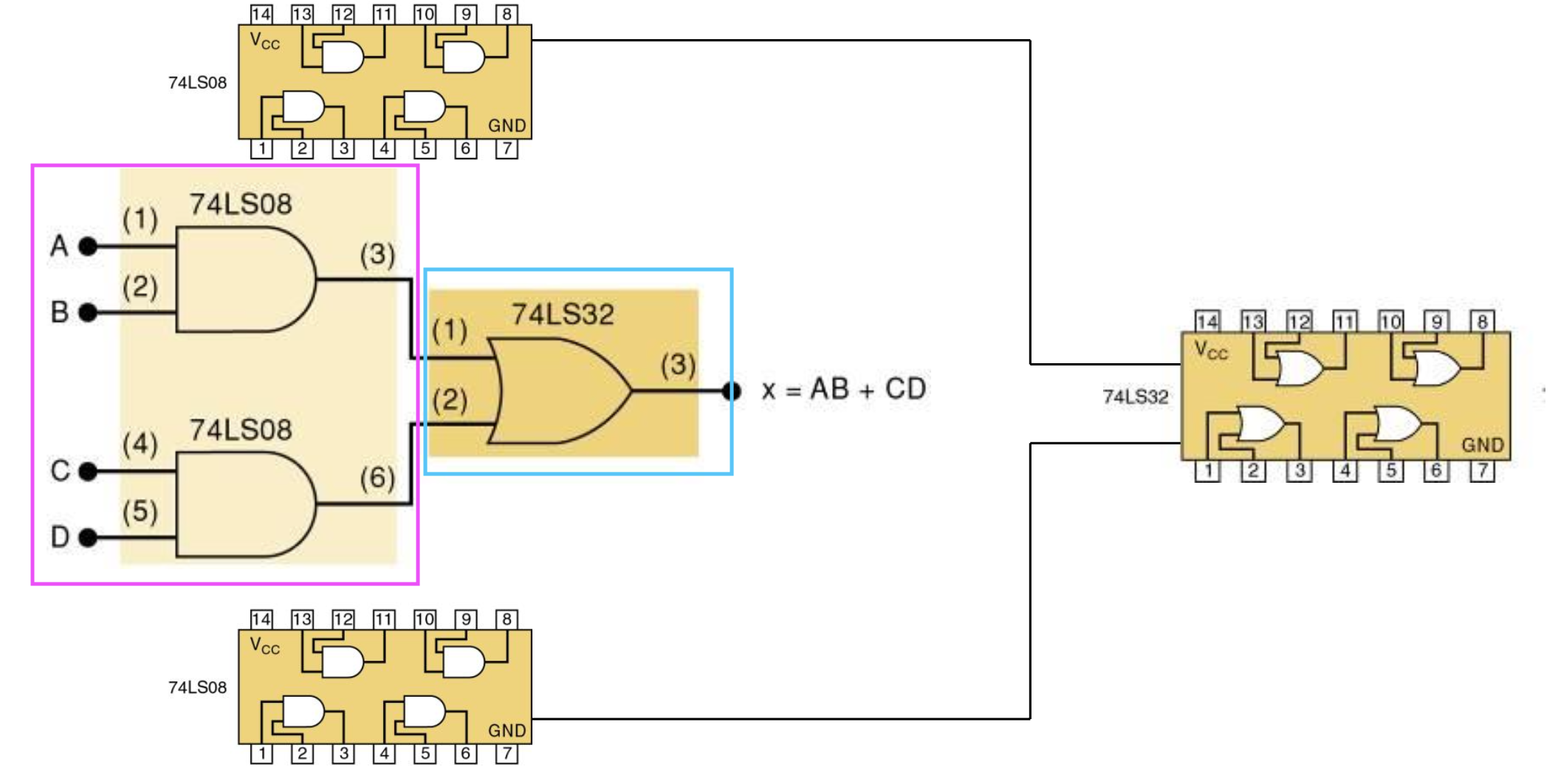
• Gate: 3개 사용
• Chip(IC Chip): 2개 사용

Possible Implementations #2 ??

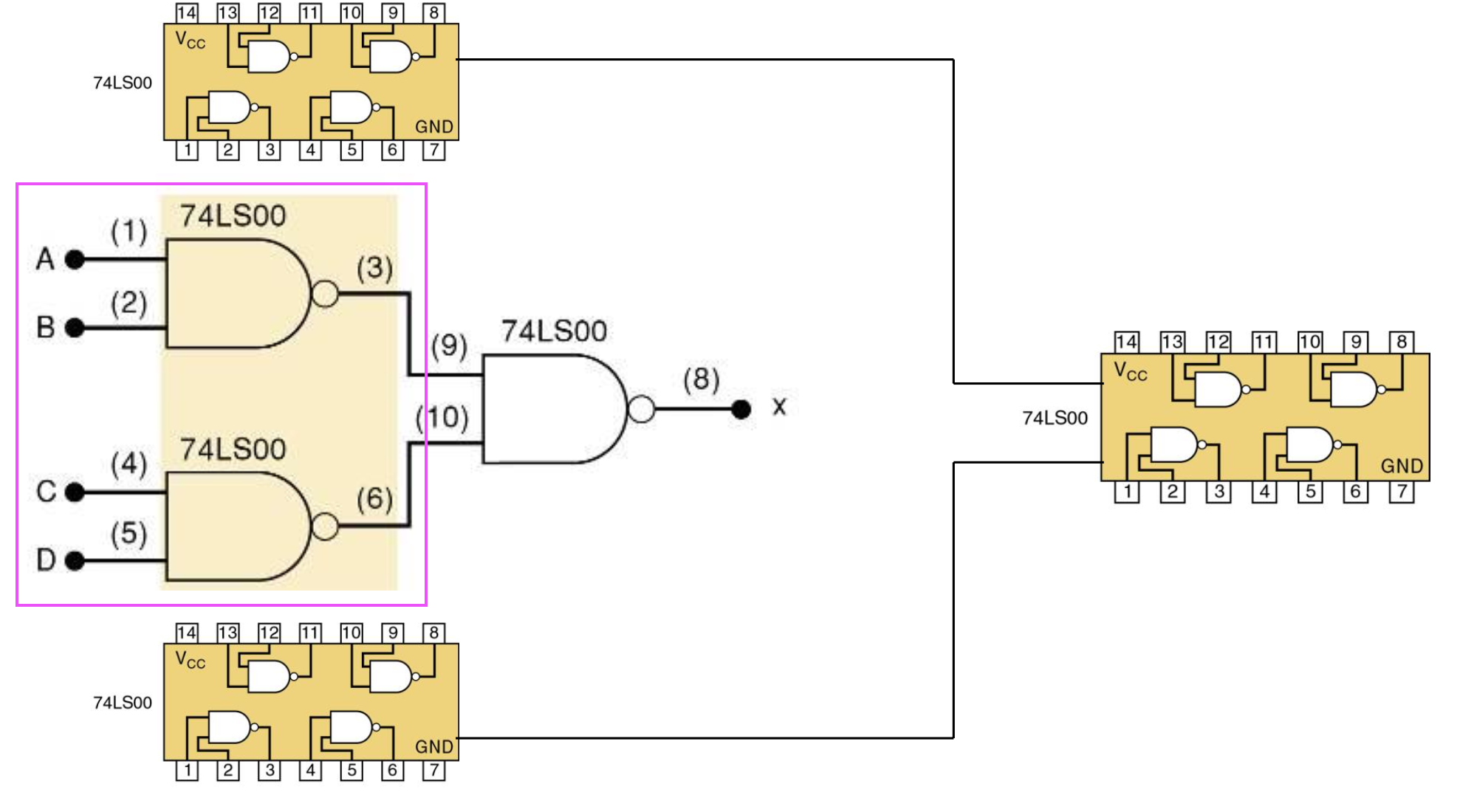
• Gate: 4개 사용
• Chip(IC Chip): 1개 사용

---

3-13 Alternate Logic-Gate Represetation

1. Bubble 은 Non-gate 를 가르킨다.

2. AND 와 OR 게이트는 버블 반대로 하면 같은 게이트가 된다.
   

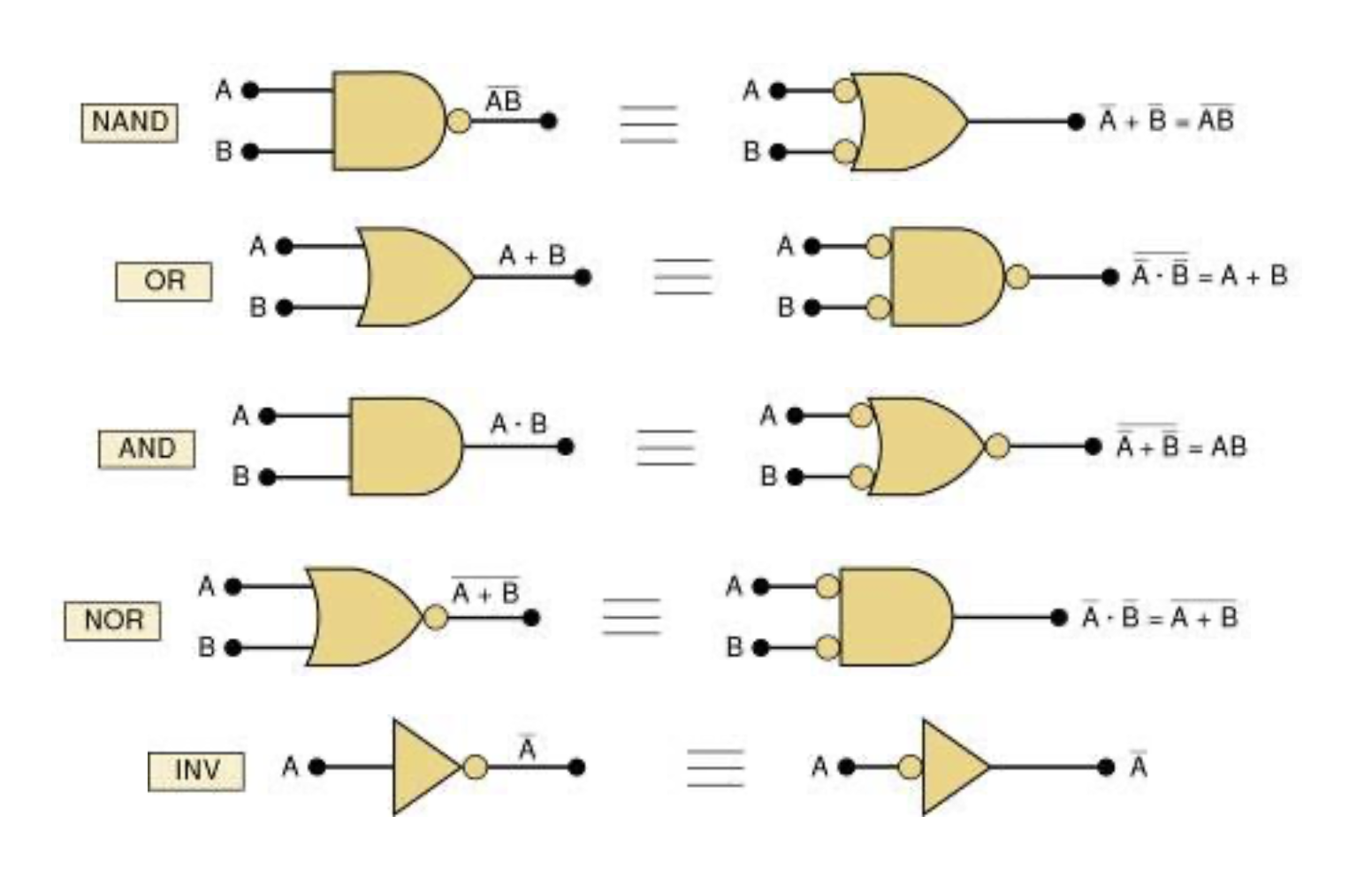
Active-HIGH

an input/output has no inversion bubble.

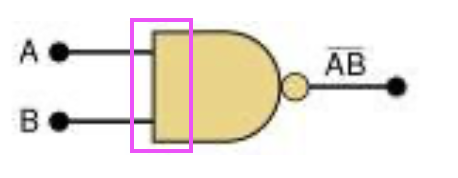
버블이 둘 다 붙어있지 않은 게이트

Active-LOW

an input or output has an inversion bubble.

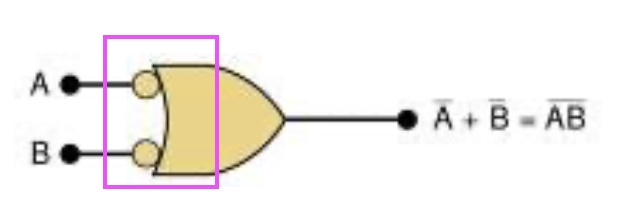
버블이 둘 다 붙어있는 게이트

두 NAND Gate symbol의 해석 차이

NAND Gate

Output goes LOW only when all inputs are HIGH.
오직 모든 입력이 High 일 때만, 결과가 LOW가 된다.

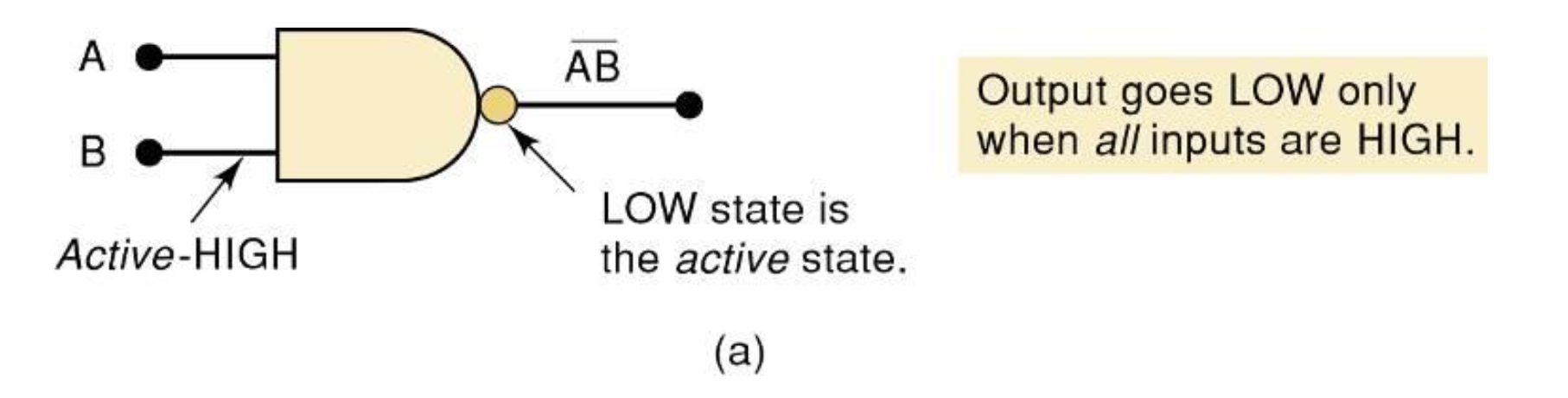
Output will be HIGH when any input will go LOW.
입력에 LOW가 있기만 해도 출력은 항상 HIGH 이다.

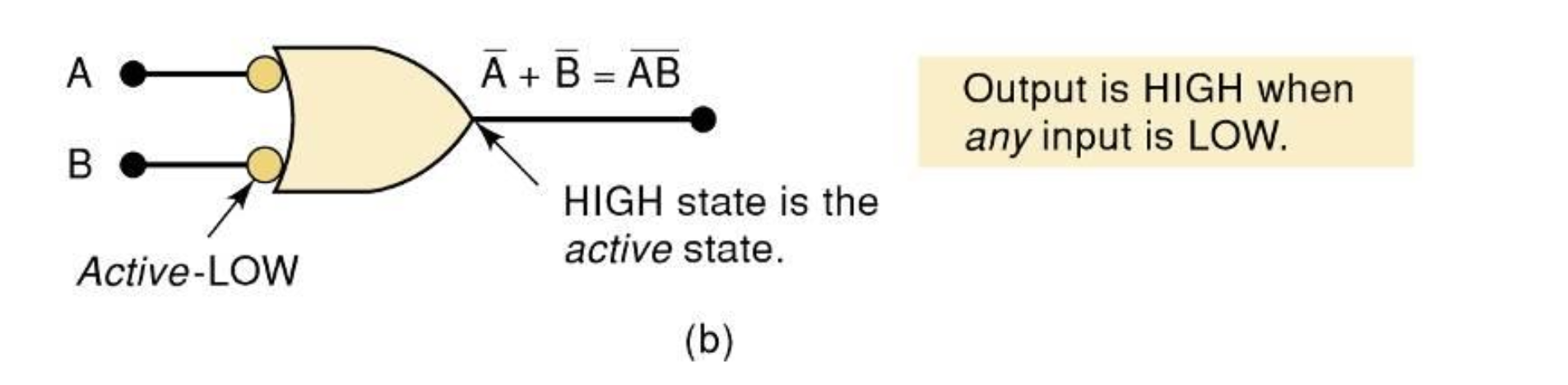
⇒ !A + !B = !(AB)

두 OR Gate symbol의 해석 차이

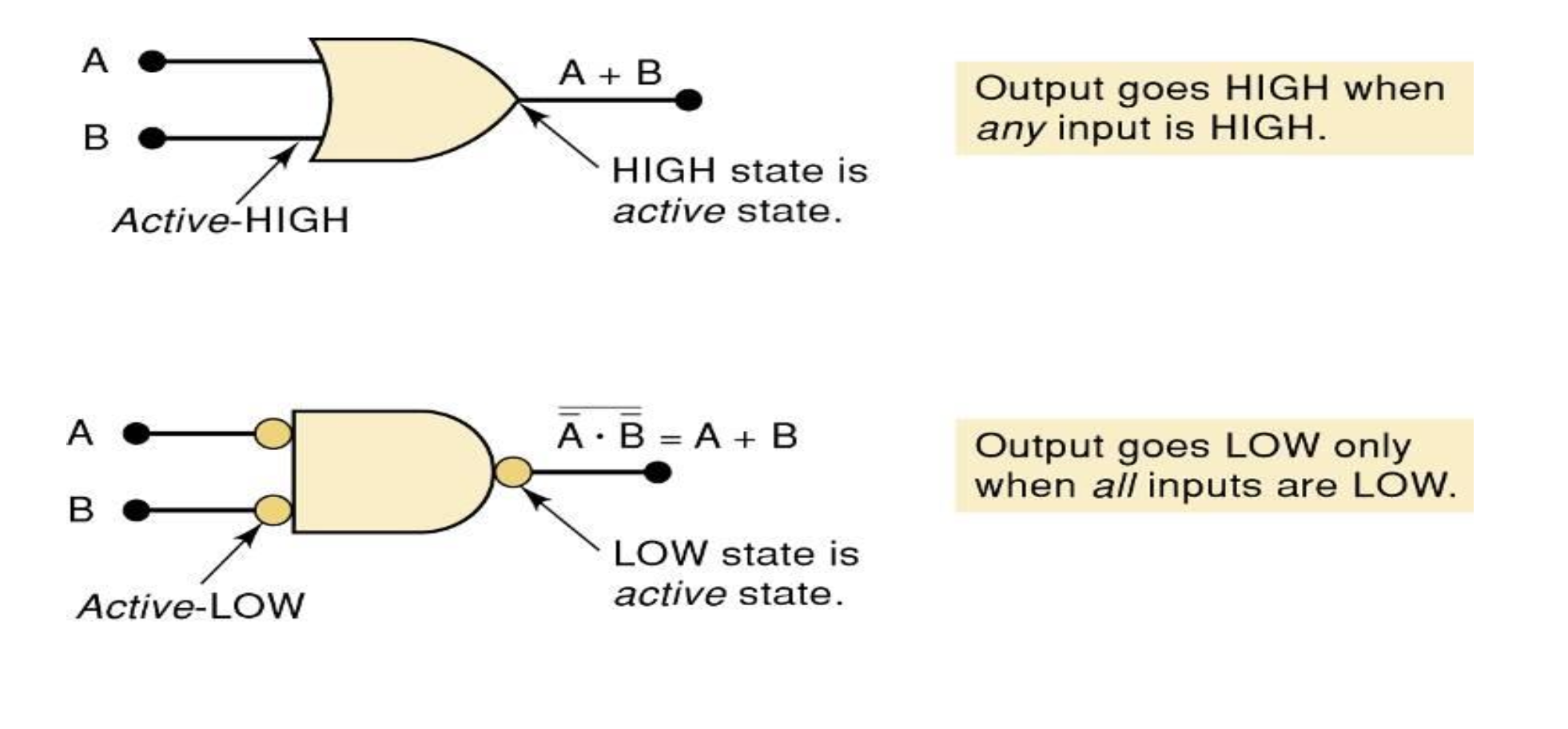
⇒ A + B = !(!A * !B)

---

5 Gates

1. OR
2. AND
3. NOT
4. NOR
5. NAND

---

Alternatice Symbols

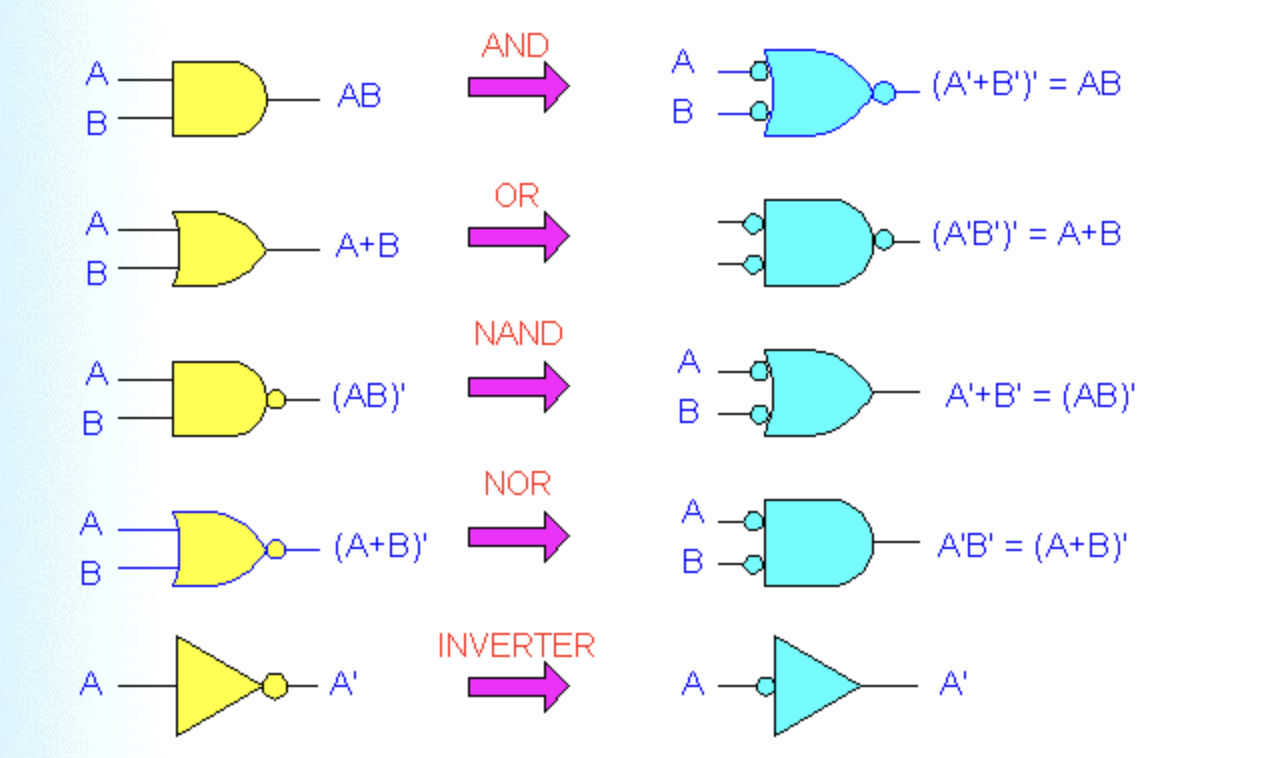
1. 마지막 NOT Gate의 INVERTER 버전은 거의 사용되지 않는다.

2. Bubble을 지우는 방법 ⇒ Alternative Symbol

---

IC = Intergrate Chip

---

3-14 Which Gate Representation to Use(중요)

Circuit diagram에서 적절한 alternative gate symbol을 사용하는 것은 Circuit operation을 훨씬 더 쉽게 사용할 수 있게해준다.

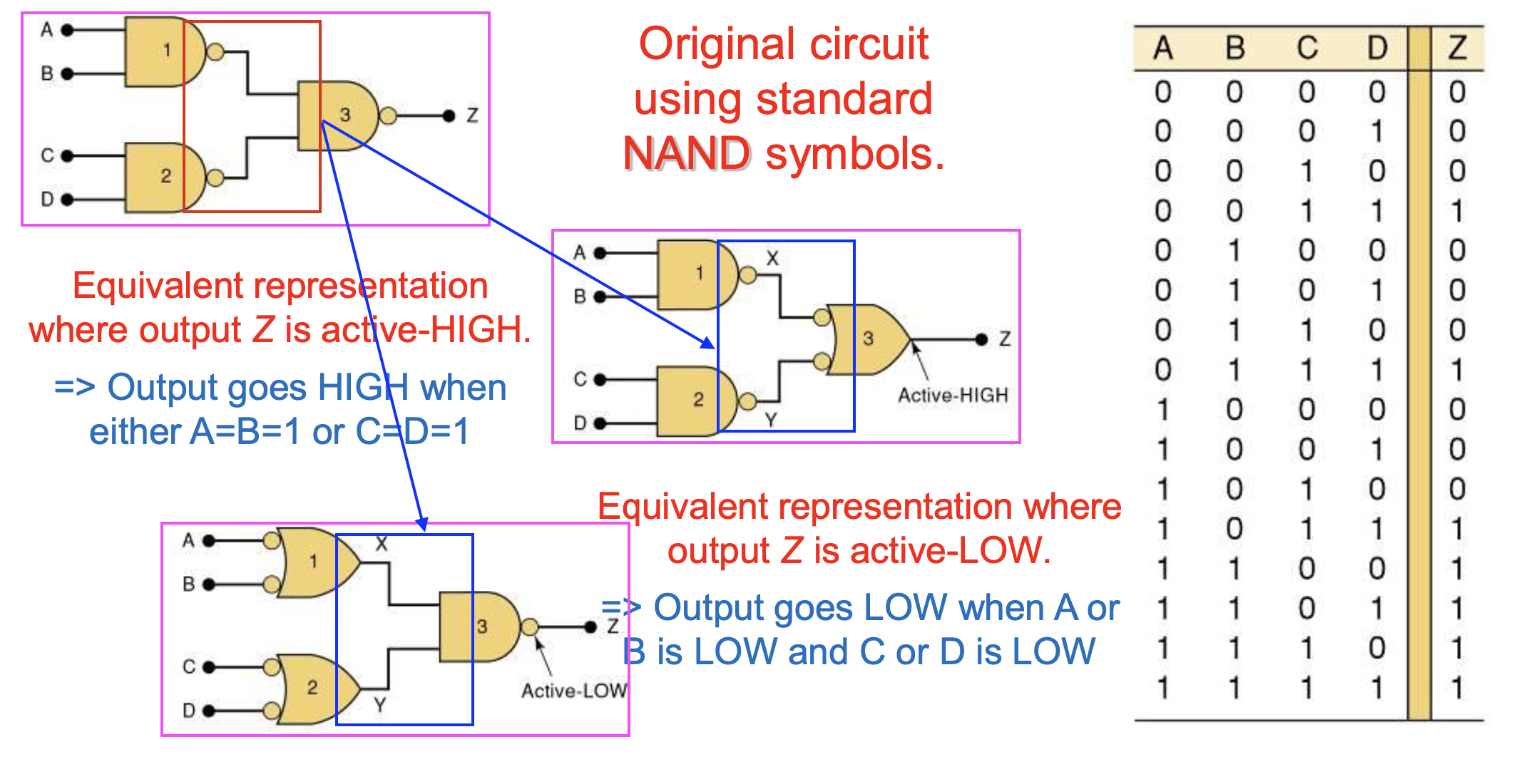
붙어있는 output과 input에 버블이 둘 다 있거나 없는 것이 좋다.
둘 다 있을 경우, 생략할 수 있다.

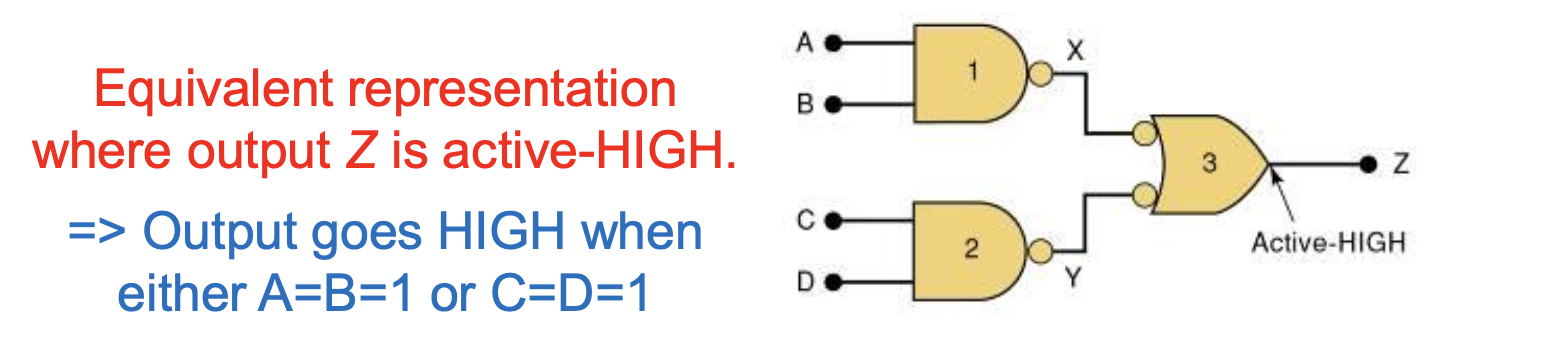
A=B=1 OR C=D=1 일 때, Output은 HIGH가 된다.

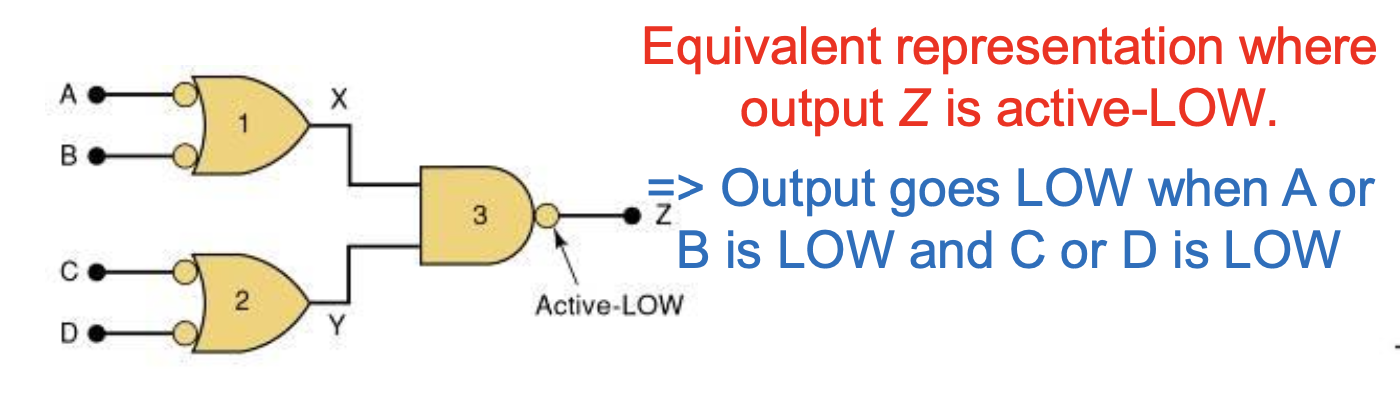
A OR B is LOW and C or D is LOW 일 때, Output은 LOW가 된다.

Logic Signal

Logic Signal이 active state(HIGH or LOW)라면 asserted(강조) 되었다고 한다.

Logic Signal이 inactive state(HIGH or LOW)라면 unasserted 되었다고 한다.

• bar가 붙으면, (active) LOW 라고 강조된다.
  

• bar가 붙지 않으면, (activate) HIGH 라고 강조된다.
  

---

가능하다면, bubble outputs은 bubble input이랑 연결되는 gate symbol을 골라라.
Nonbubble output은 nonbubble input이랑 연결되는 게 좋음.

---

알람 logic circuit

밑의 logic circuit은 Z가 HIGH일 때, 활성화된다.

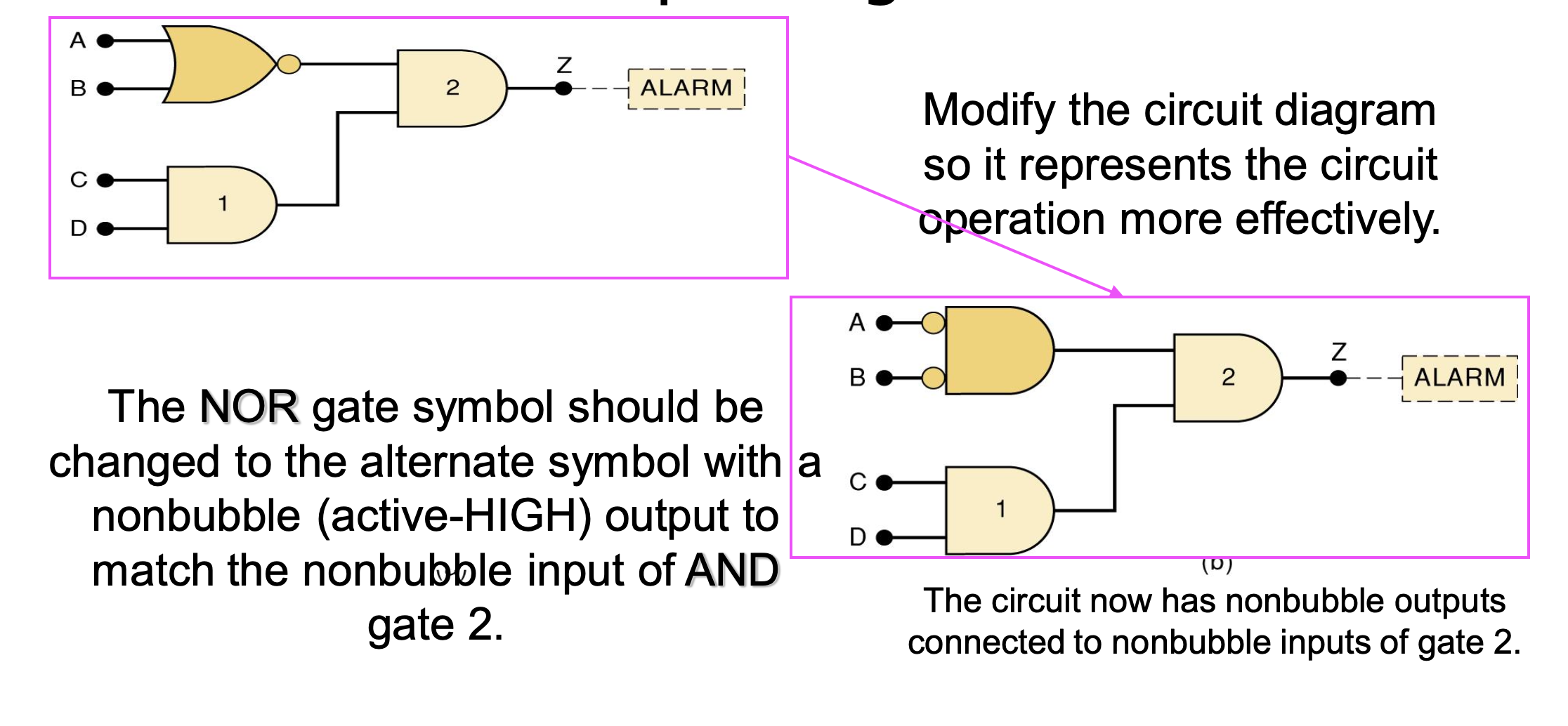
회로 다이어그램을 수정하여 회로 명령을 효율적으로 만들었다.

---

3-15 Propagation Delay
전파지연시간

Logic circuit의 속도는 Propagation Delay와 관련 있다.

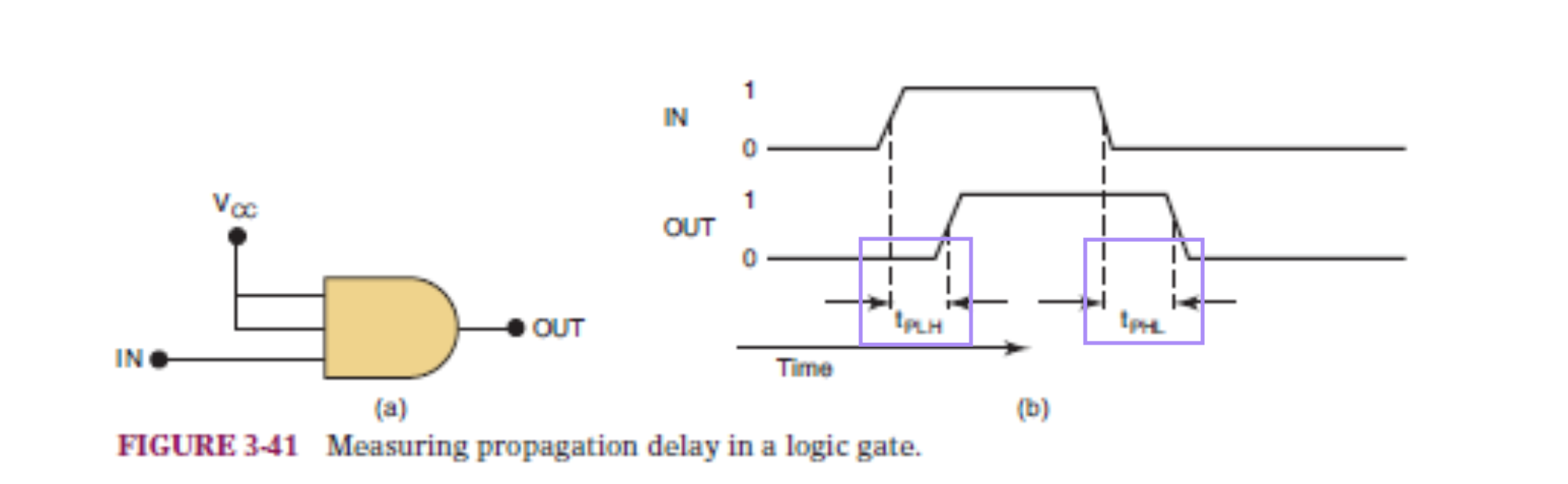
• tPLH = Propagation Low to High
• tPHL = Propagation High to Low

---

3-16 Summary of Methods To Describe Logic Circuits (중요)

다음을 사용하여 각각의 Basic Logic Functions을 표현한다.

1. Logical Statememts in our own Language
2. Truth tables
3. Traditional graphic logic symbols
4. Boolean algebra expressions
5. Timing diagrams

---

3-17 Description vs.Programming Languages

HDL (Hardware Discription Languages)

HDL을 사용하면 엄격하게 정의된 언어로 논리 회로를 나타낼 수 있다.

AHDL (Altera Hardware Description Language)

1. Altera에서 개발하여 Altera Programmable Logic Devices(PLD)를 구성한다.
2. 논리 회로를 설명하기 위한 범용 언어로 사용하기 위한 것이 아니다.

VHDL (Very High Speed Integrated circuit Hardware Description Language)

1. Developed by U.S. Department of Defense (DoD).
2. Standardized by IEEE.
3. 설계를 실제 장치를 프로그래밍하는 비트 패턴으로 변환하는 데 널리 사용된다.

HDL(Hardware Description Languages)와 Programming Language를 구별하는 것이 중요하다.

---

3-18 Implementing Logic Circuit With PLDs

PLD

Programmable Logic Devices (PLDs) 논리 기능을 수행하기 위해 다양한 방식으로 구성할 수 있는 장치이다.

→ 프로그램 장치에 대한 내부 연결이 전자적으로 이루어진다.

PLD는 전자적으로 구성되며 내부 회로는 전자적으로 함께 "wired"되어 논리 회로를 형성한다.

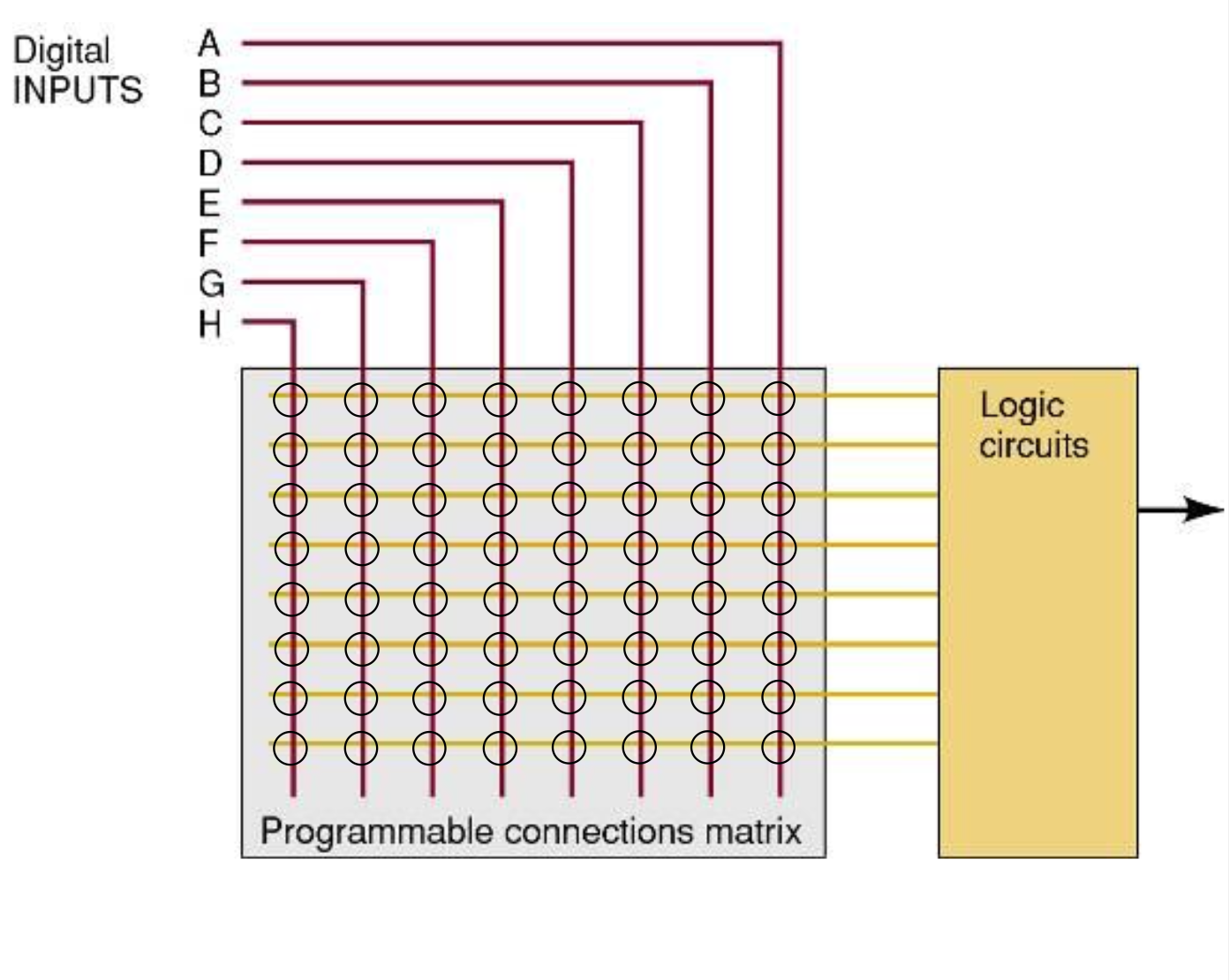
이 프로그래밍 가능한 배선은 연결되거나(1) 연결되지 않은(0) 수천 개의 연결로 생각할 수 있다.
행(수평 와이어) 및 열(수직 와이어)의 각 교차점은 프로그래밍 가능한 연결이다.

HDL은 만들 연결은 정의한다.

---

3-19 HDL Format and Syntax

컴퓨터들에 의해 해석되어진 언어들은 엄격한 syntax (구문) 규칙을 따라야한다.

• syntax 는 요소들의 순서를 나타낸다.