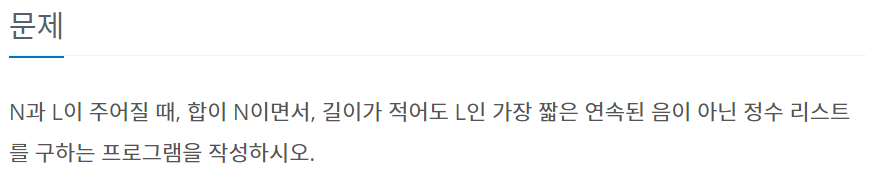
문제

풀이 과정

처음에 문제 봤을 때는 알고리즘 시간때 배웠던 LIS 문제랑 비슷해보여서 LIS 문제같이 푸는건가 싶었는데 그게 아니라 수학 공식을 활용해서 풀었다.
LIS 문제에서는 마지막 원소의 정보만 기억하면 됐는데, 이 문제에서는 시작점의 정보를 기억해야한다.
원소는 연속되어야 하고, 길이는 L 이상을 만족해야 한다.
그러면 N이라는 합을 만족시키고 길이가 적어도 L 이상인 수열의 시작점을 찾아야 한다.
시작점을 x라고 두면, 연속된 수열의 끝나는 지점은 x+L이라고 둬야 한다.
그러면 시작점은 어떻게 찾을까?
수열의 합 공식을 이용해서 시작점을 찾았다.
시작점을 찾고 나면 시작점부터 x+L-1까지를 출력하면 된다.
시작점 x는 (N - ((i - 1) * (i) / 2)) / i 이다.
시작점을 찾았으면 시작점부터 x+L-1까지의 연속된 구간의 합이 주어진 N과 맞는지 비교하는 함수 호출하여 N의 합과 맞는지 확인한다.
이후 맞으면 for문 돌려서 시작점부터 증가시킨 값을 출력한다.

코드

package backjoon;

import java.io.IOException;
import java.util.Scanner;


public class sequence_1024 {
    public static int sumofN(int x,int L){ int sum=0;
        for(int i=0;i<L;i++){
            sum+=x+i;
        }
        return sum;
    }
    public static void main(String[] args) throws IOException {
        int N, L ;
        int x ;
        Scanner sc=new Scanner(System.in);
        N=sc.nextInt();
        L=sc.nextInt();
           for(int i=L;i<100;i++) {
               x = (N - ((i - 1) * (i) / 2)) / i;
               if(N==sumofN(x,i)&&x>=0) {
                   for (int j = 0; j < i; j++) {
                       System.out.println(x + j);
                   }
                   break;
               }
               else
               {  System.out.println(-1);}
           }

        }

    }