🐰풀이 결과
def solution(triangle):
for i in range(1, len(triangle)):
for j in range(i+1):
if j==0: # 숫자가 가장 왼쪽에 있을 때
triangle[i][j] += triangle[i-1][j]
elif j==i: # 숫자가 가장 오른쪽에 있을 때
triangle[i][j] += triangle[i-1][-1]
else: # 가운데 부분에 있을 때
triangle[i][j] += max(triangle[i-1][j-1], triangle[i-1][j])
return max(triangle[-1])🐰풀이 과정
Dynamic Programming 동적 계획법 문제였다.
DP문제는 상향식 풀이법? 하향식 풀이법? 그런 것이 있는데
모르겠다. 일단 풀이 흐름을 이해하는 것이 먼저였기에..
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
이 배열들 각각의 위치에 대각선 방향에 있는 숫자들을 더한 값을 저장해 놓을까 하는 생각을 하였다. 구현은 못했지만 ^_^
근데 풀이법에 거의 접근은 하였다.
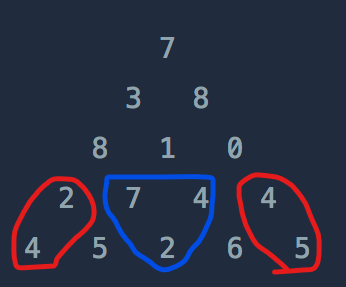
아래 사진을 봐보자
나의 풀이는 아래에서 위로 올라가며 계산식을 triangle 이라는 배열에
저장할 것이다.
정수 삼각형은 한 자리에서 왼/오 대각선으로 밖에 이동하지 못한다.
그렇다면 이때, 삼각형의 가장자리 빨간 동그라미 친구들은 선택지가 하나 밖에 없다. 위로만 갈 수 있다.
그래서
1. 숫자가 가장 왼쪽에 있을 때
2. 숫자가 가장 오른쪽에 있을 때의 경우를 찾아
그들은 자신의 바로 위 대각선의 있는 숫자들과 더해질 수 있도록 하면 된다.
파란 동그라미 친구들도 봐보자,
이들은 갈수있는 경우가 두가지 이다 왼쪽으로 가거나 오른쪽으로,
우리는 거쳐간 숫자가 최대가 되도록 하는 수를 return해야 한다.
그러면 큰 수가 있는 대각선으로 덧셈을 해나가도록 해야 한다.
그러므로 내 앞에 있는 두개의 숫자 중 가장 큰 숫자로 갈 수 있도록 Max()를 걸어두면 된다.
=> triangle[i][j] += max(triangle[i-1][j-1], triangle[i-1][j])
이렇게 덧셈이 끝난 숫자들은 triangle 배열의 각 자리에 들어가게 된다.
가장 마지막에는 모든 덧셈이 끝난 가장 최대의 수가 저장되어 있다.
그러므로 triangel[-1]을 리턴하면 된다.
