Big O Notation
- 빅오 표기법의 필요성에 대하여
- 빅오가 무엇인지
- 빅오 표기법을 표현하는 법
- "시간 복잡성"과 "공간 복합성"에 대해
- 빅오 표기법을 사용한 여러가지 알고리즘 평가
- 로그에 대하여
빅오 소개
빅오 표기법의 필요성
빅오의 핵심은 여러가지 코드를 서로 비교하고 성능을 평가하는 방법에 있다.
코드를 분류하거나 비교할 수 있는 시스템에 있어 빅오 표기법이 목적을 갖는다.
- 코드의 성능을 이야기할 때 정확한 전문 용어를 사용하는 것이 중요
- 여러 접근법의 장단점을 이야기할 때도 유용
- 코드를 디버그 할 때 느리게 만드는 것을 이해하는 것 중요
- 빅오를 이해하면 비효율적인 코드를 찾을 때 유용
- 인터뷰에 왕왕 나옴
예시
// 해결 책 1
// 해결 책 1
function solution1(n) {
let total = 0;
for (let i = 1;i <= n; i++){
total+= i
}
return total;
}
// 대략 time elapsed 141425.35490000597
// 해결 책 2
function solution1(n) {
return n * (n+1)/2
}
// 대략 time elapsed 0.00010000000894069671
let t1 = performance.now()
solution1(1000000000)
let t2 = performance.now()
console.log(`time elapsed ${(t2 - t1) / 1000} sec`) 어떤 게 더 나은 코드인가?
더 나은 코드의 의미
- 더 빠른 것?
- 메모리를 얼맘나 사용하는지?
- 얼마나 더 읽기 좋은지?
위의 두개의 코드를 속도 측면에서 얼마나 더 좋은지 어떻게 비교할 수 있을까
코드 시간 재기
시간에 문제
- 우선 기기마다 다른 방식으로 시간을 기록하여 완전히 믿을 수 없다
- 똑같은 기계가 다른 시간을 기록할 수 있다.
- 빠른 알고리즘에있어서는 속도 측정 정확도가 충분하지 않을 수 있다.
따라서 코드를 비교할 때 시간을 비교하는 것엔 문제가 있을 수 있다.
연산 갯수 세기
시간이 아니라면 무엇을 써야하는 가?
-
코드가 실행 될 때 걸리는 정확한 시간을 초로 측정하기 보단 컴퓨터가 처리해야하는 연산 갯수를 세면 된다.
-
그렇게 되면 알고리즘을 어떤 알고리즘은 실행될 때 연산은 5번 어떤건 7개를 해야한다면 걸리는 시간과 기기엔 변동이 있을 수 있지만 시간은 항상 연산의 갯수에 달려 있을 것이다.
시간 보다 컴퓨터가 실행할 수 있는 간단한 연산들의 갯수들을 세는 것


-
해당 함수의 연산을 세는 방법엔 여러가지가 있지만 간단하게 5n + 2로 표현 가능하다. 하지만 빅오를 볼 땐 이러한 정확한 숫자가 중요한게 아니라 전체적인 추세를 보는 것이다.
-
N이 커질 수록 연산의 갯수도 시간도 비례적으로 늘어난다는 것을 알 수 있다.
시간 복잡도 시각화
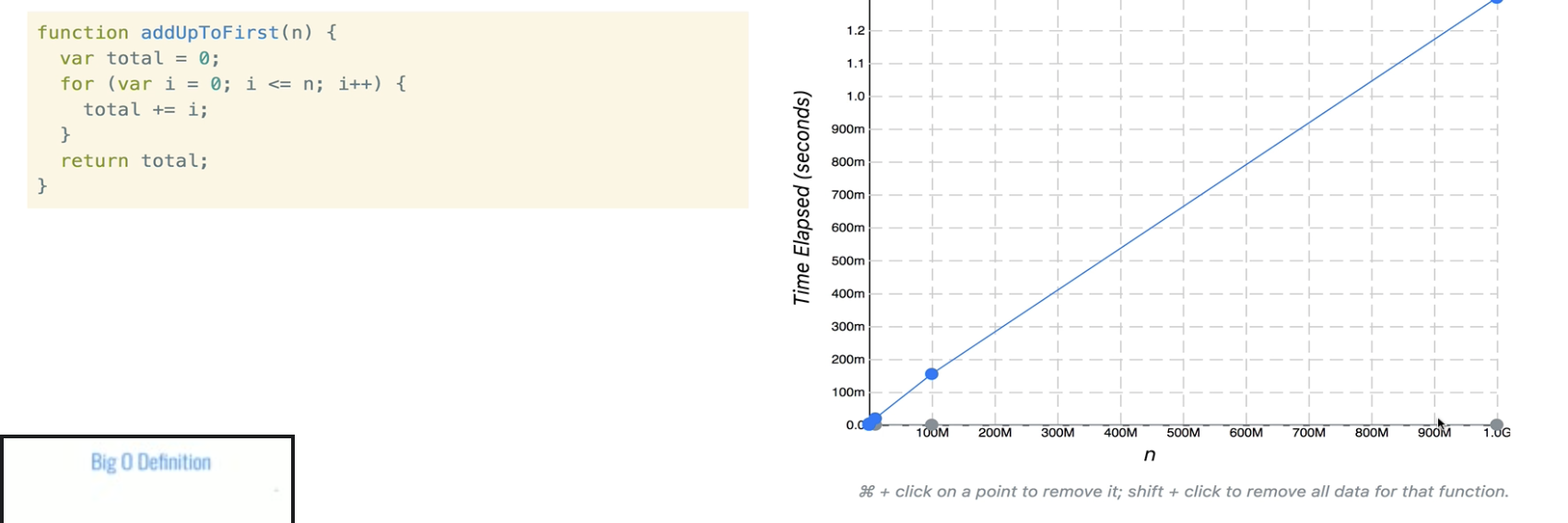
- 첫번째는 n의 값이 늘어났지만 실행되는 시간에 영향을 받지 않는 반면
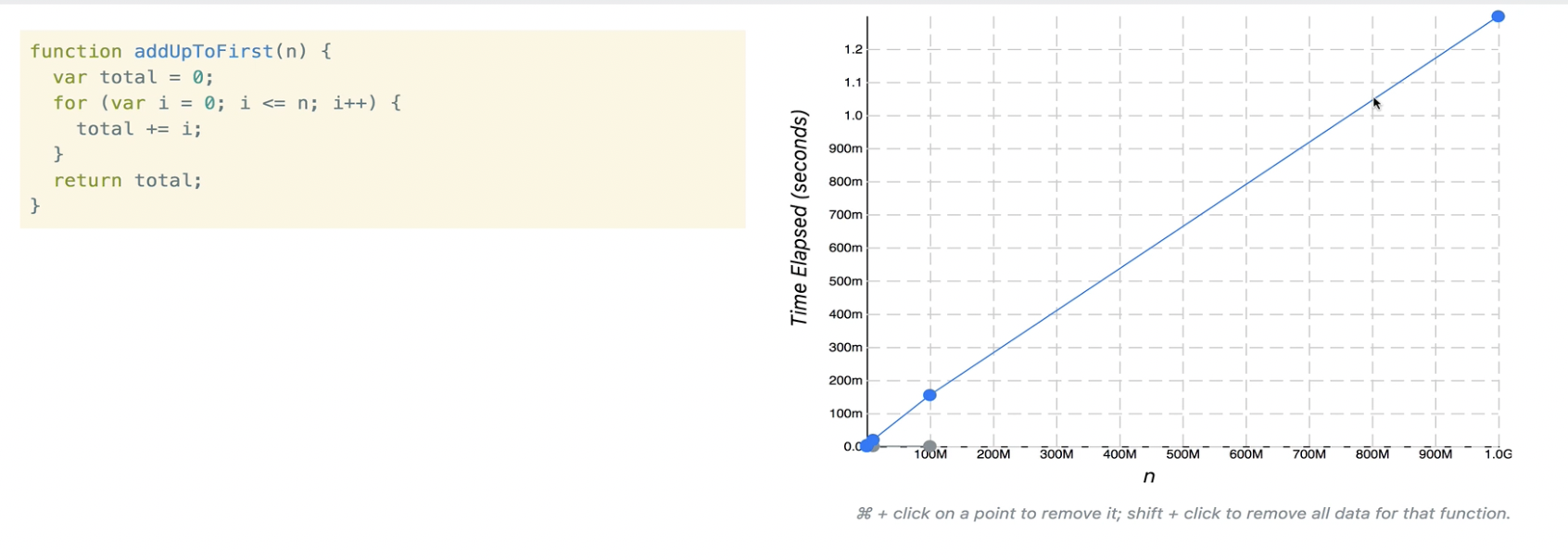
- 두번째는 실행되는 시간이 N의 값이 늘어나는 것과 비례하게 거의 1:1비율로 선형으로 늘어난다
빅오 정식 소개
- 대략적으로 숫자를 세는 것의 붙인 공식적인 표현
- 정식으로 입력된 내용이 늘어날 수록 알고리즘에 실행 시간이 어떻게 변하는지를 설명하는 공식적인 방식
- 빅오는 어떤 펑션의 입력 값이 늘어나는 것과 펑션 실행 시간이 변하는 관계,
입력의 크기와 실행시간의 관계를 의미 - 오로지 전반적인 추세에 주목을 하는 것
빅오의 정의 ? N이 커질 수록 컴퓨터가 f(n) 상수 곱하기 f(n)보다 간단한 연산을 덜 해야한 다면 그 알고리즘을 O(f(n))이라고 표현
쉽게 말해 f(n)=n은 입력과 실행 시간의 관계를 의미

- 선형 일 수 있으며 n의 값이 커질 수록 실행 시간도 늘어날 수 있음
- 실행 시간이 이차 제곱이거나 상수 일 수 도 있으며 아니면 완전히 다를 수 도 있다.
중요한 건 빅오는 실행시간이 갖을 수 있는 최대치이며
일반적으로 가장 높은 실행 시간 값들을 의미

- n의 값이 커질 수록 이 경우엔 아무 변화가 없으며 실행 시간은 변하지 않는다. O(1)
- 실행 시간이 1:1 비율로 늘어나며 연산의 갯수는 n의 곱과 연결되어있다. O(n)

function solution3(n) {
console.log('up')
for (let i = 0; i< n; i++){
console.log(i)
}
for (let j= n-1; j>=0; j--){
console.log(j)
}
console.log('down')
}- 이 역시도 O(n)이다.
function solution4(n) {
for (let i = 0; i< n; i++){
for (let j= 0; j< n; j++){
console.log(i,j)
}
}
}


- 그러나 이 경우엔 n이 커질 수록 실행 시간이 n제곱의 값으로 늘어나 상당한 차이가 난다.
- n이 커질수록 n곱하기 n만큼 늘어난다. 이것이 지수 곡선
빅오 표현식 단순화
모든 연산을 다 세어 정확한 갯수는 중요하지 않으며 전체적인 추세를 중요시한다
5n+2면 단지 n, 단지 추세가 그래프 선이 n의 값과 비례한다는 것
규칙
- 표현식을 단순화하는 가장 중요한 건 대략정인 정확한 그림이기에 상수화는 중요하지 않다.
- 작은 연산들도 중요햐지 않다.
빅오의 복잡도를 분석할 땐 매우 복잡해진다.
1.산수는 상수이며 이는 덧셈, 뺄셈, 곱셈, 나눗셈을 포함 모두 상수 시간에 포함한다.
2. 변수 배정도 상수이다.
3. 인덱스를 사용해서 엘리먼트를 접근하는 것 역시 상수
4. 루프가 있으면 복잡도가 루프의 길이 곱하기, 즉 루프 안에 있는 연산들이 된다.

빅오 그래프
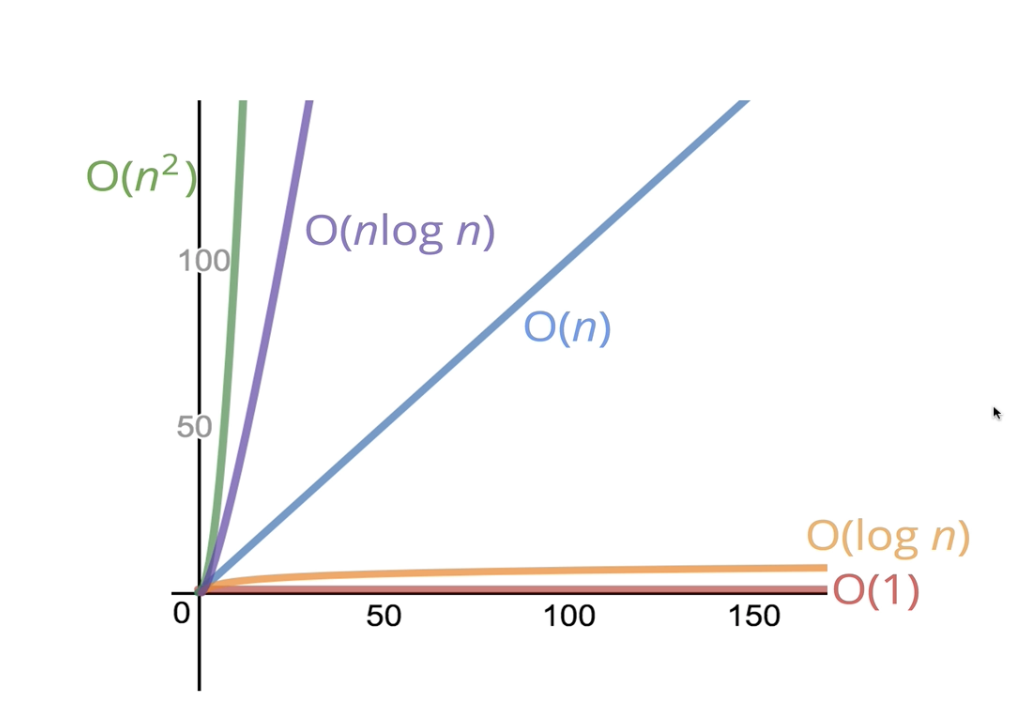
- O(1) , 수평 선으로 상수 실행 시간이 있으면 좋다.
- O(N)은 전반적인 추세
- O(n2)은 가파른 추세
