빅오 표기법

• 시간 및 알고리즘 공간 복잡도 분석을 위한 빅오 표기법 개념
• 시간(실행시간)과 공간(사용된 메모리) 관점에서 알고리즘 구현을 분석하는 법 이해

---

1. 빅오 표기법 기초

빅오 표기법

• 알고리즘 최악의 경우 복잡도를 측정
• n은 입력의 개수를 나타냄
• 알고리즘 구현 시 빅오 표기법이 해당 알고리즘이 얼마나 효과적인지 나타내기에 빅오 표기법이 중요
  

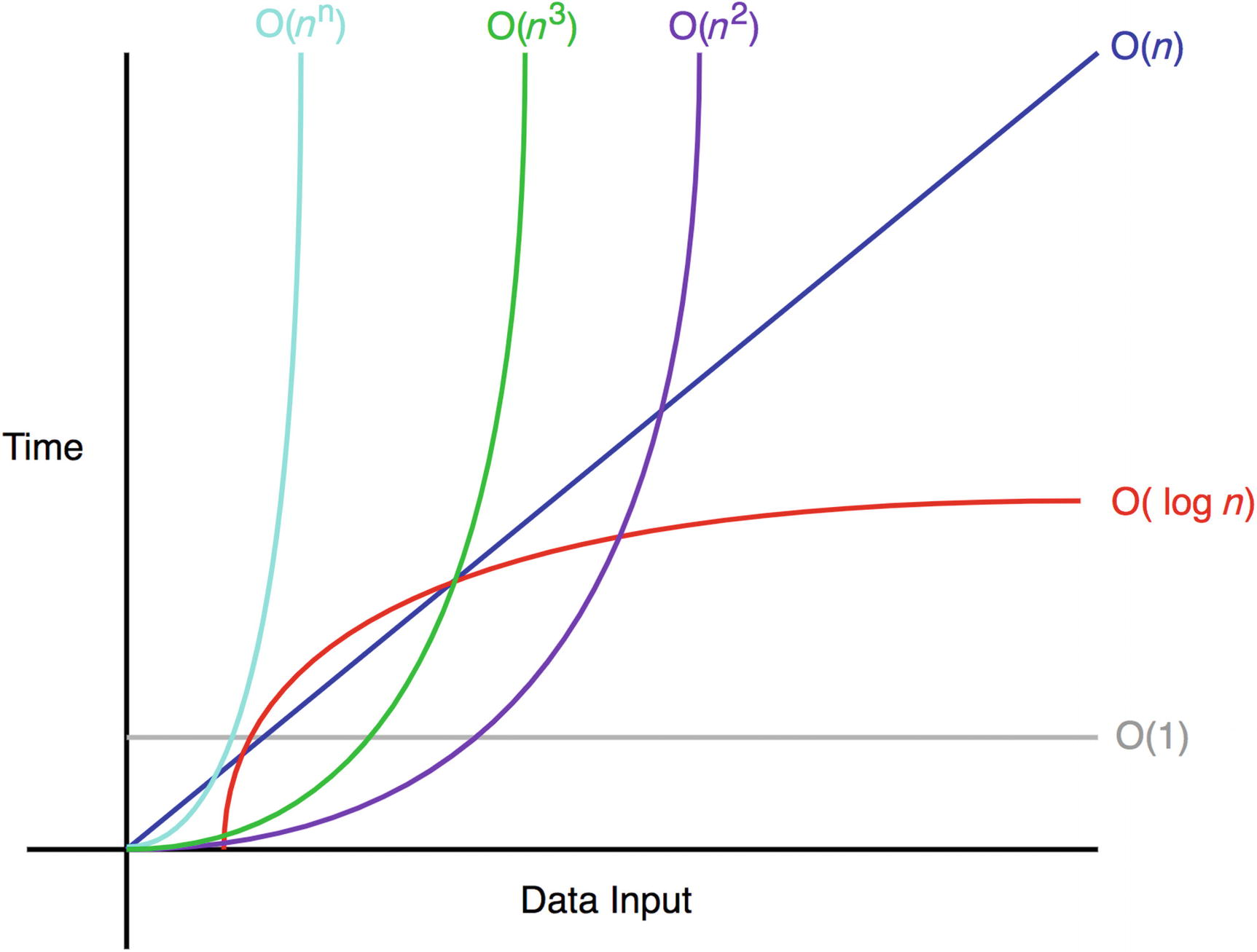
일반적인 예시

1. O(1)

• O(1)은 입력 공간에 대해 변하지 않아 상수 시간이라 부름
• 배열에 있는 항목 인덱스 사용해 접근하는 경우가 그 예시

2. O(n)

• 선형 시간이며 최악의 경우 n번의 연산을 수행해야하는 알고리즘에 적용
• 0부터 n-1까지 숫자 출력하는 경우가 그 예시

function exampleLinear(n) {
    for (var i = 0; i < n; i++) {
        console.log(i);
    }
}

3. O(n^m)

• m에 2면 2차 사긴이고 3이면 3차 시간

function exampleQuadratic(n) {
    for (var i = 0; i < n; i++) {
        console.log(i);
        for (var j = i; j < n; j++) {
            console.log(j);
        }
    }
}
function exampleCubic(n) {
    for (var i = 0; i < n; i++) {
        console.log(i);
        for (var j = i; j < n; j++) {
            console.log(j);
            for (var k = j; k < n; k++) {
                console.log(k);
            }
        }
    }
}

4. O(log n)

• 로그 시간 복잡도를 지닌 알고리즘 예는 2의 2승부터 n승까지 항목 출력 시
• 로그 시간 복잡도 효율은 백만 개의 항목과 같이 큰 입력이 있는 경우에 분명하여 n이 백만이여도 단 19개의 항목만 출력

function exampleLogarithmic(n) {
    for (var i = 1; i < n; i=i*2) {
        console.log(i);
    }
}
exampleLogarithmic(10)
// 2,4,8,16,32,64

---

2. 빅오 표기법 규칙

• 알고리즘의 시간 복잡도를 f(n)이라고 표현하면 n은 입력의 개수, f(n)은 필요한 시간, f(n)space는 필요한 공간(추가적인 메모리)를 나타냄
• 알고리즘 분석 목표는 f(n)을 계산함으로써 알고리즘 효율성 이해

f(n)을 계산하는데 도움되는 규칙

1_1. 계수 법칙

• 상수 k가 0보다 클 때, f(n)이 O(g(n))이면 kf(n)은 O(g(n))이며 이를 계수 법칙이라 함
• 입력 크기 n과 관련되지 않은 계수 제거하고 n이 무한으로 가까워지는 경우 다른 계수는 무시

1_2. "상수 제거하라"

• 입력 크기와 연관되지 않은 상수를 전부 무시
• 빅오에서 입력 크기가 클 시 계수를 무시하여 가장 중요한 법칙 중 하나
• 즉 5f(n)과 f(n) 모두 동일한 O(f(n))이라는 빅오 표기법 지님

function a(n){
    var count =0;
    for (var i=0;i<n;i++){
        count+=1;
    }
    return count

• 위 코드는 f(n)=n으로 count에 숫자를 n번 더하기에 함수의 시간 복잡도는 O(n)

function a(n){
    var count =0;
    for (var i=0;i<5*n;i++){
        count+=1;
    }
    return count;
}

• 위 코드는 f(n)=5n으로 0부터 5n까지 실행되지만 위 두 코드 예시 모두 O(n) 빅오 표기법 지님
• n이 무한대 또는 아주 큰 수에 가까워질 때 네 개의 연산이 추가적으로 존재한다 해서 달라지는 것은 없기 때문
• n이 충분히 클 때 위 코드가 n번 수행되며 빅오 표기법에서 모든 상수는 무시 가능

function a(n){
    var count =0;
    for (var i=0;i<n;i++){
        count+=1;
    }
    count+=3;
    return count;
}

• 위 코드는 f(n)=n+1으로 마지막 연산 count+=3으로 인해 +1이 추가되었지만 여전히 O(n)의 빅오 표기법
• 추가된 연산이 입력 n에 영향 받지 않고 n이 무한대로 가까워질수록 추가된 연산 무시

2_1. 합의 법칙

• f(n)이 O(h(n))이면 g(n)은 O(p(n))이면 f(n)+g(n)은 O(h(n)+p(n))임
• 결과값인 시간복잡도가 두 개의 다른 시간 복잡도의 합이라면 결과값인 빅오 표기법 역시 두 개의 다른 표기법 합을 의미

2_2. "빅오를 더하라"

• 시간 복잡도를 더할 수 있는 것으로 두 개의 다른 알고리즘을 포함하는 상위 알고리즘이 있다면 해당 상위 알고리즘의 빅오 표기법은 해당 상위 알고리즘에 포함되는 두개의 알고리즘의 합
• 단, 합의 법칙을 적용한 다음 계수 법칙이 적용된다

function a(n){
    var count =0;
    for (var i=0;i<n;i++){
        count+=1;
    }
    for (var i=0;i<5*n;i++){
        count+=1;
    }
    return count;
}

• 각 루프의 시간 복잡도는 개별적으로 계산된 다음 더해져 f(n)=n, f(n)=5n을 더해 결과값은 6n지만 여기에 계수 법칙을 적용하면 최종적 결과는 O(n)=n

3_1. 곱의 법칙

• f(n)이 O(h(n))이면 g(n)은 O(p(n))이면 f(n)g(n)은 O(h(n)p(n))임
• 두 개의 다른 시간 복잡도를 곱할 때 빅오 표기법 역시 곱해지는 것을 의미

3_2. "빅오를 곱하라"

• 빅오가 어떤 식으로 곱해지는지에 관한 것

function (n){
    var count =0;
    for (var i=0;i<n;i++){
        count+=1;
        for (var i=0;i<5*n;i++){
            count+=1;
        }
    }
    return count;
}

• 두 개의 중첩 for 루프를 포함하여 해당 중첩 for 루프에 곱의 법칙이 적용되어 f(n)= n*5n으로 내부 루프에 의해 5n번 실행되고 내부 루프가 외루 루프에 의해 n번 실행되므로 결과는 5n^2번 연산이 일어나고 계수 법칙이 적용되어 O(n)=n^2

4. 전이 법칙

• f(n)이 O(g(n))이면 g(n)은 O(h(n))이면 f(n)은 O(h(n))임
• 동일한 시간 복잡도는 동일한 빅오 표기법을 지님을 타나내기 위한 방법

5_1. 다항 법칙

• f(n)이 k차 다항식이면 f(n)은 O(n^k)임
• 직관적으로 다항 법칙은 다항 시간 복잡도가 동일한 다항 차수의 빅표기법을 지님

5_2. "빅오의 k승"

• 다항 시간 복잡도가 동일한 다항 차수를 지닌 빅오 표기법을 지님을 나타냄

function a(n){
    var count =0;
    for (var i=0;i<n*n;i++){
        count+=1;
    }
    return count;
}

• 2차 시간 복잡도를 지닌 for 루프 존재 시 n*n회 실행되기 때문인데 f(n)=n^2이 된다.

요약

• 빅오는 알고리즘 효율을 분석 및 비교 시 중요
• 빅오 분석 위해서 코드를 살펴보고 빅오 표기법을 단순화하고자 다음 규칙(법칙) 적용
  - 계수/상수 제거(계수 법칙)
  • 빅오 더하기(합의 법칙)
  • 빅오 곱하기(곱의 법칙)
  • 루프 조사해 빅오 표기법 다항 결정(다항 법칙)