• 자바스크립트 숫자 연산과 숫자 표현, Number 객체, 일반적인 숫자 알고리즘, 무작위 숫자 생성
• 프로그래밍 언어에서 숫자 연산 덕분에 숫자 값 계산 가능, 자바스크립트 숫자 연산 목록은 아래와 같음
  - + : 덧셈
  • • : 뺄셈
  • / : 나눗셈
  • • : 곱셈
  • % : 나머지 연산

1. 숫자 체계

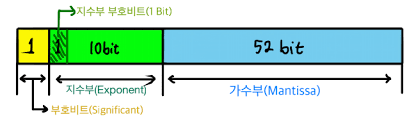
• 그림과 같이 숫자에 대해 64비트 부동 소수점 표현 사용
• 다음 예에서 값은 40으로 부호 비트가 1이면 해당 숫자가 음수 다음 여덞개의 비트는 지수 값 e를 나타내며 마지막으로 나머지 52비트가 분수 값을 나타냄
• 십진분수로 인해 자바스크립트에서 부동소수점 체계가 반오림 오류를 일으킬 수 있는데 0.1과 0.2를 정확히 표현할 수 없어 0.1 + 0.2 === 0.3의 결과는 false임

0.1 + 0.2 === 0.3; // 'false'

• 0.1을 64비트 부동수소점 숫자로 제대로 표현할 수 없는 이유 이해를 위해 이진 표기법을 이해해야함
• 이진 표기법으로 십진 수를 표현할 때 문한 개의 수가 필요한 경우 가 많아 이로 인해 이진주사 2^n으로 표현(n은 정수)
• 0.1을 계산하려 할 시 긴 나눗셈이 끝나지않고 계속되어 이진수로 1010은 10인데 0.1(1/10)을 계산하려면 소수점 아래 수가 무한히 생김

2. 자바스크립트 숫자 객체

• 자바스크립에는 위 같은 문제 해결 위해 도움되는 Number 객체의 내장된 속성이 있 음

2_1. 정수 반올림

• 자바스크립트가 모든 숫자를 나타낼 때 부동소수점을 사용하기에 정수 나눗셈은 소용없음
• 예를 들어 자바에선 정수 나눗셈의 결과는 해당 나누기의 몫으로 5/4는 1이 몫이기에 결과는 1이지만 자바스크립트에선 5/4의 결과는 부동소수점인 1.25이다
• 자바에선 명시적으로 정수를 정수형으로 선언해야하기에 결과가 부동소수점이 될 수 없어 정수 나눗셈을 원하면 다음중 하나를 사용

Math.floor(0.9); // 0 - 가장 가까운 정수로 내림
Math.floor(1.1); // 1
Math.round(0.49); // 0 - 가장 가까운 정수로 반올림
Math.round(0.5); // 1
Math.round(2.9); // 3
Math.ceil(0.1); // 1 - 가장 가까운 정수로 올림
Math.ceil(0.9); // 1
Math.ceil(21); // 21
Math.ceil(21.01); // 22

2_2. Number.EPSLION

• Number.EPSLION은 두 개의 표현 가능한 숫자 사이의 가장 작은 간격을 반환해 이는 부동소수점 근사치르 활용해 분수가 제대로 표현되지 않는 문제를 해결하는데 유용

function numberEquals(x, y) {
    return Math.abs(x - y) < Number.EPSILON;
}
0.1 + 0.2 == 0.3 // false due to little difference in floating point
numberEquals(0.1 + 0.2, 0.3); // true

• 위 함수는 두 수의 차이가 Number.EPSLION보다 작은지 검사해 작으면 true를 반환
• Number.EPSLION이 두 개의 표현 가능한 숫자 사이의 최소 차이라는 것을 기억 즉, 0.1+0.2와 0.3의 차이는 Number.EPSLION보다 작음

2_3. 최대치

• Number.MAX_SAFE_INTEGER는 가장 큰 정수 반환

Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2; // true
Number.MAX_SAFE_INTEGER + 1.111 === Number.MAX_SAFE_INTEGER + 2.022; // false

• 두 수는 더 이상 커질 수 없기에 true를 반환하지만 부동소수점에 사용하면 제대로 동작하지 않아 false를 반환

• Number.MAX_VALUE는 가능한 가장 큰 부동 소수점을 반환

Number.MAX_VALUE + 1.111 === Number.MAX_VALUE + 2.022; // true

• Number.MAX_SAFE_INTEGER와 달리 위 코드는 배정밀도 부동소수점 표현을 사용하고 부동소수점에 대해서도 잘 동작

2_4. 최소치

• Number.MIN_SAFE_INTEGER는 가장 작은 정수를 반환

Number.MIN_SAFE_INTEGER - 1 === Number.MIN_SAFE_INTEGER - 2; // true
Number.MIN_SAFE_INTEGER - 1.111 === Number.MIN_SAFE_INTEGER - 2.022; // false

• 두 수가 더이상 작아질 수 없기에 true를 반환하지만 부동소수점과 함께 사용하면 제대로 동작하지 않음

• Number.MIN_VALUE는 가장 작은 부동소수점 수를 반환
• Number.MIN_VALUE가 가능한 가장 작은 부동소수점이기 때문에 음수가 아니라 실제로 Number.MIN_VALUE는 Number.MIN_SAFE_INTEGER보다 크며 Number.MIN_VALUE는 0에 가장 가까운 부동소수점이기에 다음과 같은 코드가 가능

Number.MIN_VALUE - 1 == -1; // true

• 위 코드가 true인 이유도 0 - 1 === -1과 비슷하기 때문

2_5. 무한

• Number.MAX_VALUE보다 큰 유일한 건 Infinity고 Number.MIN_SAFE_INTEGER보다 작은 유일한 것은 -Infinity

Infinity > Number.MAX_SAFE_INTEGER; // true
-Infinity < Number.MAX_SAFE_INTEGER // true
-Infinity -32323323 == -Infinity -1; // true

• true로 평가되는 이유는 -Infinity보다 작아질 수 없기 때문

2_6. 크기 순서

• 자바스크립트 숫자의 크기를 가장 작은 것부터 큰 것 순으로 요약하면 다음과 같음

-Infinity < Number.MIN_SAFE_INTEGER < Number.MIN_VALUE < 0 < Number.MAX_SAFE_INTEGER < Number.MAX_VALUE < Infinity

2_7. 숫자 알고리즘

• 숫자가 소수, 소인수분해인지 판단하는 알고리즘은 숫자와 관련된 가장 많이 논의되는 알고리즘 중 하나

2_7_1. 소수 테스트

• 숫자가 소수인지 알아보는 방법은 n을 2부터 n-1까지 수로 나눠 나머지가 0인지 확인

function isPrime(n) {
    if (n <= 1) {
        return false
    } 
    for (let i = 2; i < n; i++) {
        if (n % i==0) {
            return false
        }
    }
    return true
}

• 위 코드에 시간 복잡도는 O(n)으로 위 알고리즘은 0부터 n까지 모든 수 확인하기 때문

• 허나 위 알고리즘은 쉽게 개선 가능한 예로 메소드가 2부터 n까지 어떤 식으로 순회되는 생각해보면 알고리즘 수행 방식에서 패턴을 찾아 더 빠르게 만들 수 있음
  - 2의 배수는 무시가능하며 최적화 가능한 부분이 더 있음
  - 소수 나열 2,3,5,7,11,13,17,19,23 ...
  - 2와 3을 제외한 모든 소스는 6k+-1(k정수) 형태를 지님
  - n이 소수인지 알아보기 위해 반복문은 n의 제곱근까지만 확인 가능하는데 n의 제곱근이 소수가 아니면 n은 수학 정의에 의해 소수가 아님

function isPrime(n) {
    if (n <= 1) return false
    if (n <= 3) return true
    // 입력된 수가 2또는 3인 경우 아래 반복문에서 다섯개 숫자 건너 띔
    if(n % 2 ==0 || n % 3 ==0) return false
    for (let i = 5; i*i <= n; i=i+6) {
        if (n % i==0 || n % (i+2) ==0) {
            return false
        }
    }
    return true
}
isPrime(123)
// 6k+-1 optimisation
function is_prime (n) {
  if (n < 3) return n > 1;
  else if (n % 2 === 0 || n % 3 === 0) return false;
  else if (n < 25) return true;
  let i = 5;
  while (i * i <= n ) {
    if (n % i === 0 || n % (i + 2) === 0) return false;
    i += 6;
    //5,7,11,13,17,19,23,25,29,31 ...
  }
  return true;
}

• 개선 된 알고리즘은 시간복잡도를 상당히 줄여 O(sqrt(n))까지 줄여줌
• 참고) 제곱근 관련, https://developerjun2.tistory.com/127

2_7_2. 소인수분해

• 어떤 숫자의 소인수분해를 구하는 알고리즘 역시 유용
• 소수는 암호화와 해싱의 기반이 되며 소인 수 분해는 주어진 숫자를 만들기 위해 어떤 소수들이 곱해져야 하는지 구하는 과정

function primeFactors(n) {
    // n이 2로 나눠진다면 나눠질 수 있는 수만큼 2가 출력
    while (n % 2 == 0) {
        console.log(2);
        n = n / 2;
    }
    // n은 이 지점에서 홀수가 확실, 따라서 수를 2개씩 증가 시킬 수 있음
    for (var i = 3; i * i <= n; i = i + 2) {
        // i가 n을 나눌 수 있는 한 계속해서 i가 출력되고 n을 i로 나눔
        while (n % i == 0) {
            console.log(i);
            n = n / i;
        }
    }
    // 다음 조건문은 n이 2보다 큰 소수를 처리
    if (n > 2) {
        console.log(n);
    }
}
primeFactors(10); // prints '5' and '2'

• 위 알고리즘은 i로 나머지가 없이 나눌 수 있는 모든 수를 출력해 소수가 함수의 입력 값으로 전달된 경우 아무 수도 출력되지 않다가 마지막 조건문에서 n이 2보다 큰지 확인 후 큰 경우 n이 출력

2_7_3. 무작위 수 생성기

• 무작위 수 생성은 어떤 조건이 어떤 식으로 동작하는지 확인하는 데 있어 중요
• 자바스크립트는 숫자 생성을 위한 내장 함수인 Math.random() 존재
• Math.random()은 0과 1 사이 부동소수점 반환하며 1보다 큰 수를 얻기 위해 Math.random()에 범위를 곱하고 나서 곱한 값에 어떤 수를 더하거나 빼서 기준 범위를 만들면 됌

Math.random() * 100; // 부동 소수점 0 부터 100
Math.random() * 25 + 5; // 부동 소수점 between 5 부터 30
Math.random() * 10 - 100; // 부동 소수점 between -100 부터 -90

• 무작위 정수 얻기 위해선 Math.floor()와 Math.round(), Math.ceil()을 사용해 부동소수점을 정수로 만들면 됌

Math.floor(Math.random()) * 100; // integer between 0 and 99
Math.round(Math.random()) * 25 + 5; // integer between 5 and 30
Math.ceil(Math.random()) * 10 - 100; // integer between -100 and -90

연습문제 1번

• x와 y,p 세개 숫자에 대해 (x^y) % p 계산 (= 모듈러 제곱거듭)
• 여기서 x는 기저, y는 지수, p는 모듈러로 모듈러 제곱 거든은 모듈러에 대해 수행하는 종류의 제곱 거듭
• 컴퓨터 과학에 유용하며 공개 키 알고리즘 분야에 사용

function modularExponentiation(base, exponent, modulus) {
    return Math.pow(base, exponent) % modulus;
}
modularExponentiation(4,3,5); // 4

• 위 코드는 큰 지수를 다룰 수 없으며 암호화 알고리즘에 사용된다는 점을 기억 시 강력한 암호의 경우 대개 기저가 최소 256비트(78개 수)
• 가령 기저가 6x10^77이고 지수가 27 모듈러가 497이면 ((6x10)^77)^27은 매우 큰 수로 32비트 부동소수점에 저장할 수 없어 수학을 좀 더 심도있기 활용한 접근법을 사용해야 함

• 임의의 a와 b에 대해 다음 속성 성립
• 위 수학적 속성 활용해 1부터 지수까지 순회하며 현재 모듈러 마지막 모듈러와 곱함으로써 매번 재계산 가능
• 기저 4, 지수 3, 모듈러 5인 경우
  c % m = (a b) % m
  c % m = [(a % m) (b % m)] % m
  4 ^ 3 & 5 = 64 % 5 = 4
  value = (lastValue x base) % module:
  value = (1 x 4) % 5 = 4 % 5 = 4
  value = (4 x 4) % 5 = 16 % 5 = 1
  value = (1 x 4) % 5 = 4 % 5 = 4
• 최종 코드는 아래와 같으며 시간복잡도는 O(n)으로 n은 지수값과 동일

function modularExponentiation(base, exponent, modulus) {
    if (modulus == 1) return 0;
    var value = 1;
    for (var i = 0; i < exponent; i++) {
        value = (value * base) % modulus;
    }
    return value;
}

연습문제 2번 - 소수 출력

• n보다 작은 모든 소수 출력 0부터 n까지 순회하면서 isPrime()이 true 평가되는 모든 소수 출력

function allPrimesLessThanN(n) {
    for (var i = 0; i < n; i++) {
        if (isPrime(i)) {
            console.log(i);
        }
    }
}
allPrimesLessThanN(15);

연습문제 3번 - 소인수 집합 확인

• 소인수가 2 또는 3 또는 5뿐인 숫자를 못생긴 숫자라 정의 시 (11개 못생긴 숫자는 1,2,3,4,5,6,8,9,10,12,15 이며 1이 관례상 포함) n개의 못생긴 숫자 찾기

• 숫자가 나머지 없이 나눠질 수 없을 때까지 숫자를 제수(2,3,5)로 나눠보고 숫자가 모든 제수에 의해 나눠질 수 있다면 나눗셈이 끝난 다음 1이 돼야 함

function maxDivide(number, divisor) {
    while (number % divisor == 0) {
        number /= divisor;
    }
    return number;
}
function isUgly(number) {
    number = maxDivide(number, 2);
    number = maxDivide(number, 3);
    number = maxDivide(number, 5);
    return number === 1;
}

• n에 대해 이를 반복하면 못생긴 숫자 목록 반환

function arrayNUglyNumbers(n) {
    var counter = 0,
        currentNumber = 1,
        uglyNumbers = [];
    while (counter != n) {
        if (isUgly(currentNumber)) {
            counter++;
            uglyNumbers.push(currentNumber);
        }
        currentNumber++;
    }
    return uglyNumbers;
}
arrayNUglyNumbers(12); // [ 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16 ]

요약

• 자바스크립트 모든 숫자는 64비트 부동소수점 형태
• 가장 작은 부동소수점 증가 얻기 위해선 Number.EPSLION을 사용
• 자바스크립트 가장 큰수와 작은 수는 다음 등식과 같이 요약
  jsInfinity < Number.MIN_SAFE_INTEGER < Number.MIN_VALUE < 0 < Number.MAX_SAFE_INTEGER < Number.MAX_VALUE < Infinity
• 소수 검증과 소인수분해는 암호화 같이 다양한 컴퓨터 과학 분야에 사용되는 개념
• 무작위 수 생성 위해 Math.random()사용