
요즘 알고리즘 개념 공부를 하는데, 피보나치 수열을 여기저기서 만난다. 그래서 찾아보던 중, 피보나치 수열을 while 반복문, 재귀함수, 메모이제이션의 각 풀이법으로 아주 잘 정리한 블로그가 있어 소개를 하고자 하는데 - 영어기도 하고 해서, 여기에 다시 한 번 정리해본다. 세 풀이법의 비교를 통해 메모이제이션이 어떻게 프로그램 실행의 효율성을 달성하는지 배울 수 있었다.
🙋🏻♀️ 메모이제이션이 뭐예요?
컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다.
💡 코드 예제를 살펴보기에 앞서, 피보나치 수열 리마인드.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
자, 여기서 아무 숫자나 하나 골라보자. 그 숫자는 직전 두 숫자의 합이다.
즉, F(n) = F(n-2) + F(n-1) 과 같은 패턴을 가진다.
🙋🏻♀️ 반복문으로 피보나치 수열 풀어주세요!
짠.
function fibonacci(n) {
if(n <= 1) return n;
let cur = 1, sum = 0, temp;
while (n > 1){
temp = cur;
cur = cur + sum;
sum = temp;
n--;
}
return sum;
}피보나치 수열이 배열에 담겨있다고 생각하면, 여기서 n 은 인덱스의 역할을 하며, n번만큼 while loop가 돌게 된다. sum 이 계속 n-1 번째까지의 합을 축적해나간다. fibonacci(10) 은 반복문이 10번 돌테니, O(n)의 시간복잡도를 가지는 것을 알 수 있다.
🙋🏻♀️ 재귀함수로 피보나치 수열을 푼다면요?
짠.
function fibonacci(n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}두 줄짜리 아름다운 코드이다. 재귀함수는 반드시 탈출조건(base case) 을 설정해주어야 하는데, n이 1인 경우로 간단히 해결했다.
하.지.만! 재귀함수의 시간복잡도는 아름답지 않다. 아래와 같이 Big O notation 으로 시간복잡도를 나타낸 그래프를 보면, 이 코드는 주황색에 해당하는 O(2^n) 의 지수함수 그래프를 따르게 된다. 왜냐하면, n이 1이 아닌 이상, fibonacci 함수를 한 번 부를 때마다, 자기 자신을 2번씩 재호출하게 되므로, 흡사 binary tree 같은 형태를 가지며 함수 호출 횟수를 기하급수적으로 증식시키게 된다. 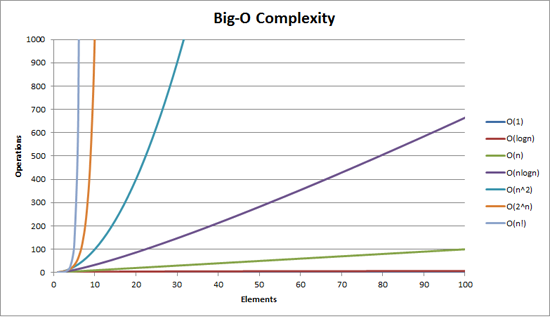
🙋🏻♀️ 메모이제이션으로 피보나치 수열을 풀 차례입니다!
옛쓰!! 👍🏼
function fibonacci(n, memo) {
memo = memo || {};
if (memo[n]) return memo[n];
if (n <= 1) return n;
return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);
}이번 코드에는 memoization 의 준말로, memo 라는 파라미터가 하나 더 생겼다. 이 memo는 데이터 저장소처럼, 피보나치로 계산한 값을 저장하는 역할을 할 것이다. 우리는 n번째 인덱스의 값을 저장하기 위해 O(n) 만큼의 공간복잡도를 추가해야하겠지만, 이미 계산한 값은 또 재귀로 계산할 필요가 없으므로 2N의 시간복잡도, 즉 O(n) 의 시간복잡도를 달성하게 된다.
앞서 소개한 블로그 원문의 주인이 Fibonacci(50) 을 기준으로 Benchmark 를 통해 퍼포먼스 비교한 값은 아래와 같다.
반복문 (While loop)
시간복잡도: O(N)
공간복잡도: Constant
함수호출횟수: 51
실행시간: 0.000001ms재귀함수 (Recursion)
시간복잡도: O(2^N)
공간복잡도: O(n)
함수호출횟수: 20.365.011.074
실행시간: 176.742ms메모이제이션 (Memoization)
시간복잡도: O(2N)
공간복잡도: O(n)
함수호출횟수: 99
실행시간: 0.000001ms
JSPerf 를 통해 Fibonacci(20) 을 기준으로 퍼포먼스 비교한 값은 아래와 같다.
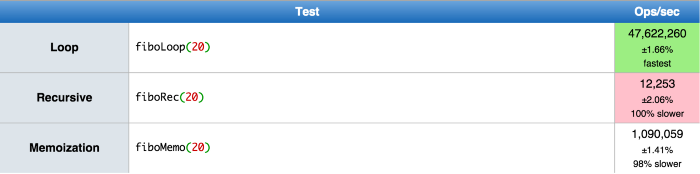
[참고 자료]
