노드 임베딩 Node2Vec. 간단한 추천시스템 구현

민죵·2024년 9월 3일

GNN공부

목록 보기

5/12

https://ysg2997.tistory.com/27 (노드 임베딩 (Node2Vec으로 간단한 추천시스템 구현))

위 링크의 게시글을 보고 공부한 내용입니다.

노드 표현 방법: DeepWalk, Word2Vec

DeepWalk
- 머신러닝 기법을 그래프에 적용하기 위한 성공적인 방법 중 하나이다.
- NLP에서 사용하는 방법과 같이 인접 노드에 대한 정보를 바탕으로, 현재 노드의 상태를 학습한다. Word2Vec기법의 아이디어를 통해, 풍부한 노드 표현을 얻는 것을 목표로 한다.

: 인접한 노드를 랜덤 하게 탐색하는 Random walk알고리즘을 적용한다. 각 스탭에서 무작위로 이웃노드를 선택하기 때문에 노드는 동일한 시퀀스에서 여러번 나타날 수 있다.

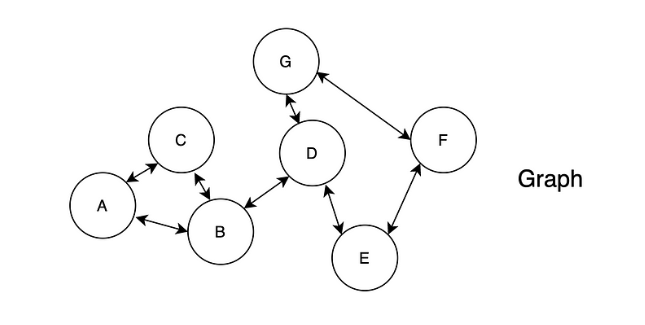
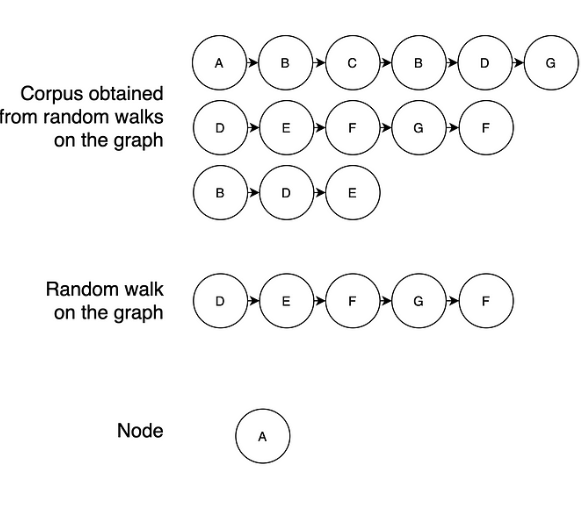
(NLP에서는 Randomwalk로 만들어진 시퀀스를 새로운 문장으로 이해할 수 있다.)

=> 노드가 무작위로 선택되더라도, 동일한 시퀀스에서 자주 함께 나타나는 것은 그들이 서로 가까이에 있다는 것을 의미한다. 이는 network homophily 이론을 기반으로한다. 따라서 서로 가까이 연결된 노드는 성질이 유사하다는 것을 의미한다. 이 아이디어는 Deep Walk 알고리즘의 핵심이다. 노드가 서로 가까울 때, 높은 유사도를 가지며 노드가 멀리 떨어져있을 때는 낮은 점수를 갖는다.

정리: Deep walk알고리즘은 Random Walk알고리즘을 기반으로한다. Random walk알고리즘은 각 스탭에서 무작위로 이웃노드를 선택하여 동일한 시퀀스에서 여러번 나올 수 있다. 여러번 나온다는 것은 서로 가까이 연결되어있고, 가까움을 유사함으로 보게된다. 빈도가 높으면 높은 유사도라고본다.

[랜덤워크 구현 코드]

그래프를 만든다.

 
# Create a graph
# 노드의 개수는 10으로 고정
# 두 노드 간의 엣지를 만드는 확률은 0.3으로 설정함
G = nx.erdos_renyi_graph(10, 0.3, seed=1, directed=False)
        # 무작위 그래프의 한 종류로, 주어진 노드 수와 엣지의 존재 확률에 따라 그래프를 생성합니다.
# Plot graph
plt.figure()
plt.axis('off')
nx.draw_networkx(G,
                 pos=nx.spring_layout(G, seed=0),
                 node_size=600,
                 cmap='coolwarm',
                 font_size=14,
                 font_color='white'
                 )

랜덤 워크 함수

랜덤 워크 함수는 시작 노드와 원하는 시퀀스의 길이 두가지 파라미터를 받는다.
매 스탭마다 랜덤하게 이웃노드를 선택한다. (np.random.choice)를 사용한다.
시퀀스의 길이만큼 반복문을 진행한다.

import random
random.seed(0)
 
def random_walk(start, length):
    walk = [str(start)]  # starting node
 
    for i in range(length):
        neighbors = [node for node in G.neighbors(start)]
        next_node = np.random.choice(neighbors, 1)[0]
        walk.append(str(next_node))
        start = next_node
 
    return walk
 
# Create a list of random walks
print(random_walk(0, 10))

### result ###
 
['0', '1', '9', '1', '0', '4', '6', '7', '6', '5', '6']

Word2Vec

karate_club_graph 그래프이론에서 유명한 소셜 데이터이다. 데이터는 두그룹으로 나누어진다.


import networkx as nx
import matplotlib.pyplot as plt
# Load dataset
G = nx.karate_club_graph()  #카라테 클럽의 소셜 네트워크를 나타내는 그래프를 생성합니다. 이 그래프에서 노드(점)는 클럽의 구성원을 나타내고, 엣지(선)는 구성원 간의 친분 관계를 나타냅니다.
 
# Process labels (Mr. Hi = 0, Officer = 1)
labels = []
for node in G.nodes:
    label = G.nodes[node]['club']
    labels.append(1 if label == 'Officer' else 0)
    
    # 각 노드(클럽 회원)에는 해당 회원이 속한 클럽이 'Mr. Hi' 그룹인지 아니면 'Officer' 그룹인지를 나타내는 레이블이 있습니다. 이 부분에서는 각 노드를 순회하며, 'Officer' 그룹이면 1을, 'Mr. Hi' 그룹이면 0을 labels 리스트에 추가합니다.
    
# Plot graph
plt.figure(figsize=(12,12))
plt.axis('off')
nx.draw_networkx(G,
                 pos=nx.spring_layout(G, seed=0),
                 node_color=labels,
                 node_size=800,
                 cmap='coolwarm',
                 font_size=14,
                 font_color='white'
                 )
#그래프를 시각화합니다.
#plt.figure(figsize=(12,12))는 12x12 크기의 플롯을 생성합니다.
#plt.axis('off')는 축을 숨깁니다.
#nx.draw_networkx() 함수는 그래프를 그립니다.
#pos=nx.spring_layout(G, seed=0)는 그래프의 레이아웃을 정의합니다. #spring_layout은 노드 간의 거리를 자연스럽게 배치하는 레이아웃입니다.
#node_color=labels는 노드의 색상을 앞서 정의한 labels 리스트에 따라 지정합니다. #coolwarm 컬러맵을 사용하여 0과 1에 해당하는 색상을 지정합니다.
#node_size=800은 노드의 크기를 설정합니다.
#font_size=14, font_color='white'는 노드 레이블의 글꼴 크기와 색상을 설정합니다.

카라테 클럽 구성원들의 관계 (gpt)

"Mr. Hi"와 "Officer" 그룹은 Zachary's Karate Club 데이터셋에 등장하는 두 파벌(faction)을 나타냅니다. 이 데이터셋은 사회학자 Wayne Zachary가 1977년에 한 카라테 클럽의 구성원들 간의 관계를 연구한 결과로 유명합니다.

배경 설명:

Zachary는 카라테 클럽에서 발생한 분열을 관찰하고 이를 네트워크로 모델링했습니다. 클럽의 지도자였던 "Mr. Hi"(가명)와 클럽의 행정 책임자였던 "Officer"(가명) 사이에 갈등이 생기면서, 결국 클럽이 두 개의 파벌로 나뉘었습니다.

Mr. Hi 그룹: 클럽의 창립자이자 지도자인 "Mr. Hi"를 지지한 사람들로 구성된 파벌입니다.
Officer 그룹: 클럽의 행정 책임자인 "Officer"를 지지한 사람들로 구성된 파벌입니다.
이 데이터셋에서는 각 클럽 구성원이 어느 그룹에 속해 있는지를 나타내는 정보가 포함되어 있습니다. 이 정보를 바탕으로 노드를 두 가지 색상으로 구분하여 시각화할 수 있습니다. 예를 들어, 코드에서 'Officer' 그룹은 1로, 'Mr. Hi' 그룹은 0으로 레이블링하여 그래프의 노드 색상을 다르게 표현한 것입니다.

따라서 이 그룹 나누기는 클럽 구성원들이 결국 어느 쪽에 가담했는지를 보여주며, 그래프 시각화에서는 각 파벌 간의 사회적 관계를 명확하게 드러내줍니다.

이후 길이가 10인 랜덤워크를 생성한다. 이때 학습을 충분하게 진행하기 위해, 각 노드별로 80번의 랜덤 한 시퀀스를 생성하였다.

  # Create a list of random walks
  walks = []
  for node in G.nodes:
      for _ in range(80):
          walks.append(random_walk(node, 10))

  # Print the first random walk
  print(walks[0])
  
  ### result ###
 
['0', '10', '0', '17', '0', '2', '13', '0', '2', '9', '33']

하나의 시퀀스는 NLP에서 길이가 10인 sentence들로 볼 수가 있다. 따라서 각 노드의 임베딩을 얻기 위해 word2vec을 사용한 코드이다.

노드 9와 유사성이 높은 애들을 출력해본다.

from gensim.models import Word2Vec

# Create Word2Vec
model = Word2Vec(walks,
               hs=1,   # Hierarchical softmax
               sg=1,   # Skip-gram
               vector_size=100,
               window=10,
               workers=1,
               seed=1)

print(f'Shape of embedding matrix: {model.wv.vectors.shape}')

# Build vocabulary
model.build_vocab(walks)

# Train model
model.train(walks, total_examples=model.corpus_count, epochs=30, report_delay=1)

# Most similar nodes
print('Nodes that are the most similar to node 9:')
for similarity in model.wv.most_similar(positive=['9']):
  print(f'   {similarity}')

# Similarity between two nodes
print(f"\nSimilarity between node 0 and 4: {model.wv.similarity('0', '4')}")

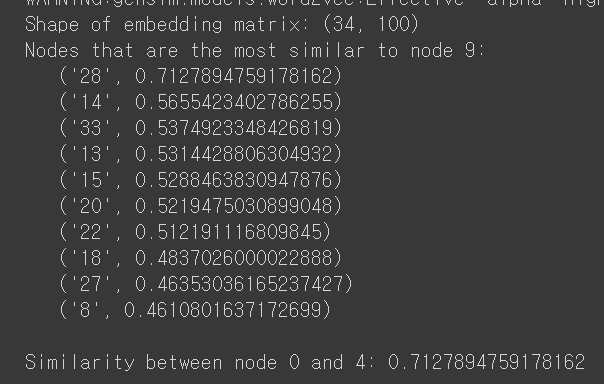
9와 28이 연관성이 높은것으로 나타난다.

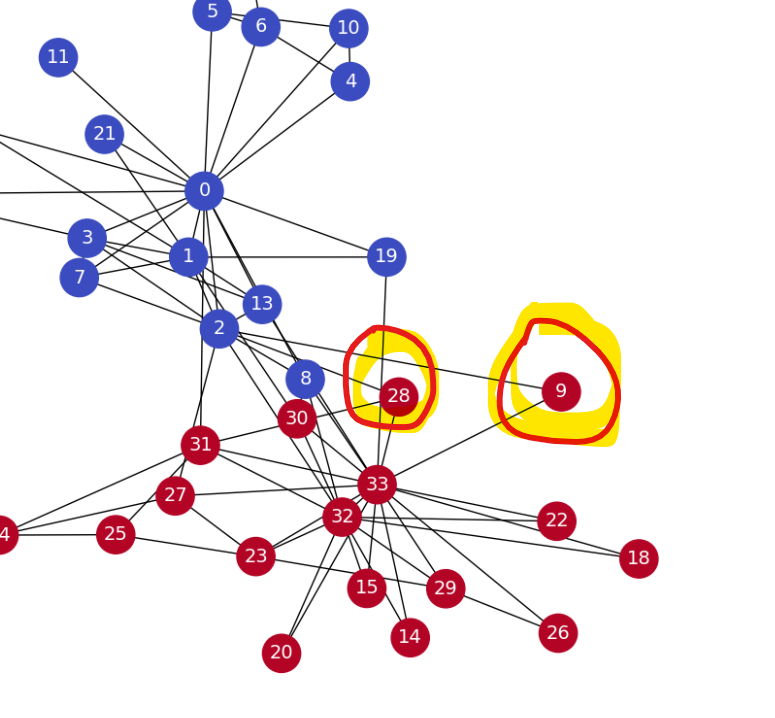
노드에 대한 임베딩: Node2Vec

Biased Node2Vec

Biased random walk는 그래프 이론 및 네트워크 분석에서 자주 사용되는 개념으로, 노드를 따라 무작위로 이동하되, 특정 조건이나 편향(bias)을 적용해 이동하는 방법을 말합니다. 이는 전통적인 random walk와는 달리, 각 이동에서 단순히 무작위로 다음 노드를 선택하지 않고, 특정 규칙이나 확률을 통해 방향성을 부여하는 방식입니다.

노드를 무작위로 선택하되, 특정 기준에 따라 이동 확률에 편향(bias)을 주는 방식입니다. 편향은 여러 방식으로 적용될 수 있으며, 일반적으로 다음과 같은 형태를 가집니다:
가중치 기반 편향: 엣지(노드 간의 연결)에 가중치가 부여되어 있으면, 가중치가 높은 노드로 이동할 확률이 높아집니다.
이전 노드 고려: 이전에 방문한 노드를 고려하여, 방문했던 노드로 돌아가지 않거나 돌아가는 확률을 낮추는 식의 편향이 적용될 수 있습니다.
노드의 특성에 따른 편향: 노드의 중요도(예: 중앙성, 차수 등)에 따라 더 중요한 노드로 이동할 확률이 높아질 수 있습니다.

Biased random walk에서 p와 q 값은 특히 Node2Vec 알고리즘에서 중요한 역할을 합니다. 이 두 파라미터는 그래프 내에서 무작위 보행을 수행할 때 탐색 방향을 조정하여, 그래프의 다양한 구조적 특성을 캡처하는 데 사용됩니다. 아래에서 p와 q 값이 무엇을 의미하는지 설명드리겠습니다.

p 값 (Return Parameter)
p는 이전에 방문했던 노드로 되돌아가는 확률을 조정하는 파라미터입니다.
p 값이 클 경우: 이전 노드로 되돌아가는 것을 어렵게 만듭니다. 따라서 이 경우 탐색이 그래프 내에서 멀리 떨어진 노드들로 이동하는 경향이 있습니다.
p 값이 작을 경우: 이전 노드로 되돌아갈 확률이 높아집니다. 이는 깊이 우선 탐색(DFS)와 유사한 동작을 하게 하여, 특정 지역(노드 근처)에 더 집중된 탐색을 수행합니다.

q 값 (In-out Parameter)
q는 현재 노드에서 새로운 노드로 이동할 때의 탐색 폭을 조정하는 파라미터입니다.
q 값이 클 경우: 그래프의 가까운 이웃 노드로의 이동 확률이 높아집니다. 이는 넓이 우선 탐색(BFS)과 유사한 탐색을 수행하게 하며, 이웃 노드들을 우선적으로 탐색합니다.
q 값이 작을 경우: 멀리 떨어진 노드로 이동할 가능성이 더 높아집니다. 이는 깊이 우선 탐색(DFS)과 유사한 방식으로, 그래프의 더 먼 영역을 탐색하게 됩니다.
p와 q 값의 조합
이 두 파라미터의 조합에 따라 탐색 경로가 다양하게 결정됩니다:
p > 1, q > 1: 탐색이 넓이 우선 탐색에 더 가깝게 이루어집니다. 탐색이 현재 노드의 이웃 노드들에 집중되며, 특정 지역에서 탐색이 멈출 수 있습니다.
p < 1, q > 1: 깊이 우선 탐색과 비슷한 방식으로, 현재 지역을 더 깊게 탐색하지만 멀리 이동하지는 않습니다.
p > 1, q < 1: 넓이 우선 탐색에 가깝지만, 더 먼 노드들로 이동할 가능성이 높아져 탐색이 지역적으로 넓게 이루어집니다.
p < 1, q < 1: 깊이 우선 탐색과 비슷하며, 탐색이 더욱 멀리 이루어집니다. 이는 그래프의 넓은 영역을 탐색하고, 전반적인 구조를 파악하는 데 유리합니다.
요약
p 값은 이전 노드로의 되돌아감(탐색의 집중도)을 조절하고,
q 값은 현재 노드의 이웃 탐색(탐색의 폭)을 조절합니다.
이 두 값을 조정함으로써, Node2Vec은 그래프의 구조를 보다 유연하고 효과적으로 탐색하여, 노드 간의 관계를 반영하는 벡터 임베딩을 생성할 수 있습니다.

이때, DeepWalk는 p와 q가 모두 1인 Node2Vec의 특별한 케이스로 이해할 수 있다.

간단한 추천시스템 구현

biased randomwalk를 사용하여 노드의 임베딩을 나타내는 Node2Vec 기법을 적용하여 간단한 추천 시스템을 구현

추천 시스템을 구현하기 위해서 유저 - 아이템의 이분 그래프를 생성해야 한다. 이 섹션에서는 간단하고 직관적인 접근 방식을 구현하였다. movielens 데이터를 사용하여 동일한 사용자가 좋아하는 영화들을 연결하였다. 이러한 정보를 그래프로 표현하여 Node2Vec을 통해 아이템인 영화 임베딩을 학습하였다.


 from io import BytesIO
 from urllib.request import urlopen
 from zipfile import ZipFile

 url = 'https://files.grouplens.org/datasets/movielens/ml-100k.zip'
 with urlopen(url) as zurl:
     with ZipFile(BytesIO(zurl.read())) as zfile:
         zfile.extractall('.')

 import pandas as pd

 ratings = pd.read_csv('ml-100k/u.data', sep='\t', names=['user_id', 'movie_id', 'rating', 'unix_timestamp'])

 movies = pd.read_csv('ml-100k/u.item', sep='|', usecols=range(2), names=['movie_id', 'title'], encoding='latin-1')

 # 4점 이상 평점을 준 레이팅 정보만 사용한다.
 ratings = ratings[ratings.rating >= 4]
 ratings

그래프 만들기


  from collections import defaultdict

  # defaultdict을 통해 자동적으로 결측 값을 무시하는 딕셔너리를 생성함.
  # 링크가 존재하는 영화를 저장하기 위해 사용함
  pairs = defaultdict(int)

  # Loop through the entire list of users
  for group in ratings.groupby("user_id"):
      # List of IDs of movies rated by the current user
      user_movies = list(group[1]["movie_id"])

      # Count every time two movies are seen together
      for i in range(len(user_movies)):
          for j in range(i+1, len(user_movies)):
              pairs[(user_movies[i], user_movies[j])] += 1

  pairs


### result ###
 
defaultdict(int,
            {(61, 33): 4,
             (61, 160): 6,
             (61, 20): 4,
             (61, 202): 4,
             (61, 171): 6,
             (61, 265): 8,
             ...

- 두 영화 페어가 20번 이상 같은 유저에 의해 시청된, 페어만을 필터링하여 그래프를 그린다.

이때 두 영화가 얼마나 가까운지를 나타내는 edge의 weight는 두 영화가 함께 시청된 횟수를 지정하였다.


# Create a networkx graph
G = nx.Graph()
 
# Try to create an edge between movies that are liked together
for pair in pairs:
    movie1, movie2 = pair
    score = pairs[pair]
 
    # The edge is only created when the score is high enough
    if score >= 20:
        G.add_edge(movie1, movie2, weight=score)
 
print("Total number of graph nodes:", G.number_of_nodes())
print("Total number of graph edges:", G.number_of_edges())

### result ###
 
Total number of graph nodes: 410
Total number of graph edges: 14936

마지막으로 Node2Vec을 적용하여 생성된 그래프에 대해 노드 임베딩을 학습한다.
각 노드를 표현하는 dimension은 64, 노드 시퀀스의 길이는 20, 시퀀스의 개수는 200, p값과 q값은 각각 2, 1이다. 이후 recommend 함수에 인자를 입력하여, 가장 유사도가 높은 노드, 즉 영화 5개를 추천해 준다.


from node2vec import Node2Vec
 
node2vec = Node2Vec(G, dimensions=64, walk_length=20, num_walks=200, p=2, q=1, workers=1)
 
model = node2vec.fit(window=10, min_count=1, batch_words=4)
 
def recommend(movie):
    movie_id = str(movies[movies.title == movie].movie_id.values[0])
    for id in model.wv.most_similar(movie_id)[:5]:
        title = movies[movies.movie_id == int(id[0])].title.values[0]
        print(f'{title}: {id[1]:.2f}')
 
recommend('Star Wars (1977)')

### result ###
 
Return of the Jedi (1983): 0.61
Raiders of the Lost Ark (1981): 0.55
Godfather, The (1972): 0.49
Indiana Jones and the Last Crusade (1989): 0.46
White Squall (1996): 0.44