문제

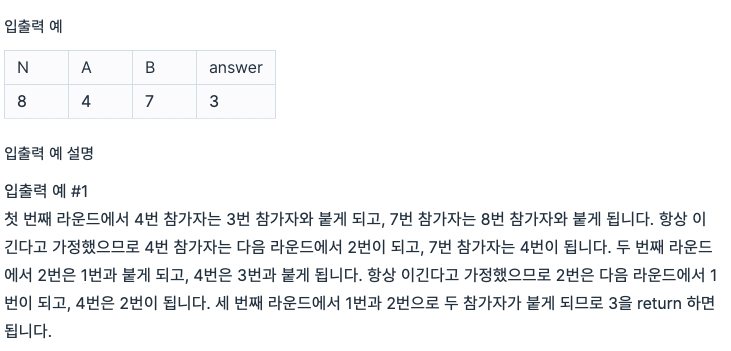
풀지 못한 이유
- 문제를 너무 복잡하게 생각해서 리스트에 대결 상대들을 묶고 한 팀씩 돌아가며 승자를 다음 라운드에 올려 이를 반복하려고 했다. (N이 최대 2^20이기 때문에 반복문을 반복적으로 사용하는(or 재귀 함수) 것은 매우 안 좋다.)
- 또한, 반복문을 돌고 있는 리스트의 값을 변경하면 안 되기 때문에 따로 리스트를 두어 다음 라운드에 올라갈 사람을 넣고 다시 그 리스트를 반복하여 결과 값을 도출하려고 했지만 구현하지 못했다.
풀이 1) ceil 이용
질문하기에서 a와 b의 값을 ceil 값으로 2로 계속 나눠주면 된다는 내용을 참고한 후 작성한 코드다. 이 풀이가 성립하는 이유는 문제에서 a와 b는 서로 붙게 되기 전까지 항상 이긴다고 가정했기 때문이다.
from math import ceil
def solution(n,a,b):
answer = 1 # 1라운드에서 시작
for i in range(n):
# a와 b를 다음 라운드 번호로 갱신
a, b = ceil(a/2), ceil(b/2)
if a == b: break # a와 b가 서로 붙음
answer += 1 # 다음 라운드
return answer문제의 입출력 예를 적용해서 살펴보자.
총 참가자는 8명이기 때문에 1라운드에서 서로의 대결 상대는 다음과 같다.
1 vs 2 | 3 vs 4 | 5 vs 6 | 7 vs 8여기서 4번 참가자와 7번 참가자는 무조건 이겨서 다음 라운드에 진출하기 때문에 다음 라운드에서의 번호는 2번과 4번이 된다. 이 부분이 for 문을 처음 돌았을 때의 상태다. a와 b의 값(참가자의 번호)을 반으로 나누고 올리면 다음 라운드에서의 두 참가자의 번호로 갱신된다.
정리하자면 1라운드에서 a는 4번, b는 7번이다. 2라운드에서 a는 2번, b는 4번이다. 3라운드에서 a와 b 모두 1번이다. 이렇게 a와 b의 값이 같아졌을 때의 라운드(answer)가 결과 값이 된다.
풀이 1) 회고
너무 간단한 풀이로 해결돼서 당황했다. 코드는 짧지만 이 방법을 생각하지 못했다. 문제를 리스트나 딕셔너리를 이용해 풀려고 해서 더 복잡하게 생각한 것 같다. 다음부턴 단순하게 접근해 보려고 하자.
풀이 2) XOR 연산 이용
다른 사람의 풀이에 있는 방법이다.
a와 b의 위치를 2진수로 표현했을 때, 서로 가까워지려면 두 비트가 같을 때 0을, 다를 때는 1을 더하는 XOR 연산을 수행하면 된다. (XOR 연산은 서로 다를 때 1을 출력하는 연산이다.)
def solution(n,a,b):
return ((a-1)^(b-1)).bit_length()문제의 입출력 예를 적용하여 살펴보면, (a-1)^(b-1)는 3^6이고, 연산 결과는 5가 된다. 여기서 a와 b의 값을 1씩 빼주는 이유는 참가자의 위치를 인덱스 형태로 바꾸는 것이다. 즉, 리스트에서 시작 인덱스가 0이기 때문에 4번째 원소의 인덱스가 3인 것과 같다.
3(4번째 참가자의 인덱스): 011
6(7번째 참가자의 인덱스): 110
XOR 연산 결과: 101 => 5그리고 bit.length()로 XOR 연산 결과의 길이를 알아낸다. 즉, 이 값이 두 참가자가 만나는 라운드인 셈이다.
풀이 2) 회고
아니 이건 더 짧다. 단 2줄로 문제를 해결하다니, 도대체 어떻게 하면 이런 사고를 가질 수 있는지. 컴퓨터가 아니냐는 댓글에 정말 공감했다. 이번 문제는 얼마나 참신하고 컴퓨터식 사고를 지니고 있는지를 보는 문제인 것 같다.

