[Swift | 프로그래머스 Lv.2] 거리두기 확인하기 (2021 카카오 채용연계형 인턴십)

Minji Kim·2021년 12월 31일
level2swift거리두기확인하기카카오코딩테스트프로그래머스
0

프로그래머스 코딩테스트 Lv.2

목록 보기
6/12
post-thumbnail

문제

문제 설명

개발자를 희망하는 죠르디가 카카오에 면접을 보러 왔습니다.

코로나 바이러스 감염 예방을 위해 응시자들은 거리를 둬서 대기를 해야하는데 개발 직군 면접인 만큼
아래와 같은 규칙으로 대기실에 거리를 두고 앉도록 안내하고 있습니다.

  1. 대기실은 5개이며, 각 대기실은 5x5 크기입니다.
  2. 거리두기를 위하여 응시자들 끼리는 맨해튼 거리가 2 이하로 앉지 말아 주세요.
  3. 단 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.
  • 맨해튼 거리 : 두 테이블 T1, T2가 행렬 (r1, c1), (r2, c2)에 각각 위치하고 있다면, T1, T2 사이의 맨해튼 거리는 |r1 - r2| + |c1 - c2| 입니다.

예를 들어,

위 그림처럼 자리 사이에 파티션이 존재한다면 맨해튼 거리가 2여도 거리두기를 지킨 것입니다.


위 그림처럼 파티션을 사이에 두고 앉은 경우도 거리두기를 지킨 것입니다.


위 그림처럼 자리 사이가 맨해튼 거리 2이고 사이에 빈 테이블이 있는 경우는 거리두기를 지키지 않은 것입니다.


응시자가 앉아있는 자리(P)를 의미합니다.


빈 테이블(O)을 의미합니다.


파티션(X)을 의미합니다.

5개의 대기실을 본 죠르디는 각 대기실에서 응시자들이 거리두기를 잘 기키고 있는지 알고 싶어졌습니다. 자리에 앉아있는 응시자들의 정보와 대기실 구조를 대기실별로 담은 2차원 문자열 배열 places가 매개변수로 주어집니다. 각 대기실별로 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.

제한사항

  • places의 행 길이(대기실 개수) = 5
    • places의 각 행은 하나의 대기실 구조를 나타냅니다.
  • places의 열 길이(대기실 세로 길이) = 5
  • places의 원소는 P,O,X로 이루어진 문자열입니다.
    • places 원소의 길이(대기실 가로 길이) = 5
    • P는 응시자가 앉아있는 자리를 의미합니다.
    • O는 빈 테이블을 의미합니다.
    • X는 파티션을 의미합니다.
  • 입력으로 주어지는 5개 대기실의 크기는 모두 5x5 입니다.
  • return 값 형식
    • 1차원 정수 배열에 5개의 원소를 담아서 return 합니다.
    • places에 담겨 있는 5개 대기실의 순서대로, 거리두기 준수 여부를 차례대로 배열에 담습니다.
    • 각 대기실 별로 모든 응시자가 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 담습니다.

입출력 예

placesresult
[["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"], ["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"], ["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]][1, 0, 1, 1, 1]

입출력 예 설명

입출력 예 #1
첫 번째 대기실

  • 모든 응시자가 거리두기를 지키고 있습니다.

두 번째 대기실

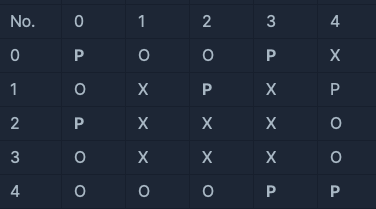
  • (0, 0) 자리의 응시자와 (2, 0) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
  • (1, 2) 자리의 응시자와 (0, 3) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
  • (4, 3) 자리의 응시자와 (4, 4) 자리의 응시자가 거리두기를 지키고 있지 않습니다.

세 번째 대기실

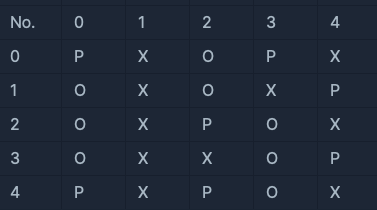
  • 모든 응시자가 거리두기를 지키고 있습니다.

네 번째 대기실

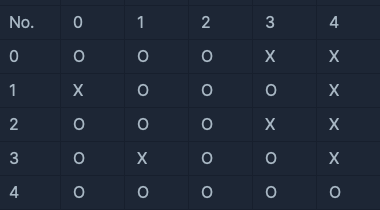
  • 대기실에 응시자가 없으므로 거리두기를 지키고 있습니다.

다섯 번째 대기실

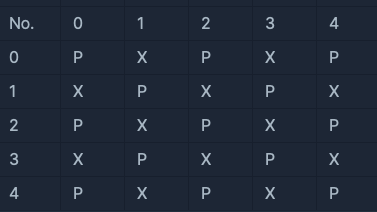
  • 모든 응시자가 거리두기를 지키고 있습니다.

두 번째 대기실을 제외한 모든 대기실에서 거리두기가 지켜지고 있으므로, 배열 [1, 0, 1, 1, 1]을 return 합니다.

제한시간 안내

  • 정확성 테스트 : 10초

풀이

나의 풀이

// TODO:
1. P, O, X의 위치 좌표를 담은 딕셔너리(location) 만들기
2. 대기실 별로 거리두기 지키는지 확인하기 - isKeepDistance
  2-1. 응시자(P) 없으면 거리두기 지킴
  2-2. 응시자(P) 있으면 P끼리 맨해튼 거리 구하기
3. 맨해튼 거리가 2 이하면 근처에 파티션 있는지 확인하기 - findPartion
  3-1. 두 좌표의 x가 같으면 y 사이에 파티션이 위치하는지
  3-2. 두 좌표의 y가 같으면 x 사이에 파티션이 위치하는지
  3-3. 두 좌표의 x, y가 모두 다르면 교차하여 확인
import Foundation

func solution(_ places:[[String]]) -> [Int] {
    var location = [String: [(Int, Int)]]()
    var arr = [(Int, Int)]()
    var result = [Int]()
    
    places.map { place in
        place.indices.map { x in
            let line = place[x].map { String($0) }
            line.indices.map { y in
                // location 딕셔너리에 값 넣기
                // ex) ["P":[(0, 0)], "O":[(0, 1)], "X":[(0, 2)]]
                if location[line[y]] == nil {
                    location[line[y]] = [(x, y)]
                } else {
                    arr = location[line[y]]!
                    arr.append((x, y))
                    location.updateValue(arr, forKey: line[y])
                }
            } // 한 행(줄) 다 돌음
        } // 대기실 한 곳 다 돌음
        
        // 거리두기 확인해서 result 배열에 Int 값 넣기
        result.append(isKeepDistance(location))
        
        // arr, location 초기화
        arr = []
        location = [:]
        
    } // 모든 대기실 다 돌음
    
    return result
}

func isKeepDistance(_ location: [String: [(Int, Int)]]) -> Int {
    var isKeep = 1
    
    // 응시자 없으면 거리두기 지키고 있으므로 1 반환
    guard let p = location["P"] else { return isKeep }
    
    // 재귀로 P(응시자) 좌표 조합 생성
    func getCombination(_ arr: [(Int, Int)], _ r: Int, _ res: inout [[(Int, Int)]], _ now: [(Int, Int)] = [(Int, Int)]()) {
        let n = arr.count
        guard n > 0 else { return }
        
        if r == 0 {
            res.append(now)
        } else if n == r {
            res.append(now + arr)
        } else {
            getCombination(Array(arr[1...]), r - 1, &res, now + [arr.first!])
            getCombination(Array(arr[1...]), r, &res, now)
        }
    }
    var pCombi = [[(Int, Int)]]()   // P(응시자) 좌표 조합
    getCombination(p, 2, &pCombi)
    
    pCombi.forEach {
        // (r1, c1), (r2, c2) = |r1 - r2| + |c1 - c2|
        let distance = ($0[0].0 - $0[1].0).magnitude + ($0[0].1 - $0[1].1).magnitude    // 맨해튼 거리
        if distance < 3 {
            // 맨해튼 거리 2이하이면 findPartion 함수로 근처에 파티션있나 확인
            guard let x = location["X"] else { return isKeep = 0 }
            if !findPartion($0, x) {
                isKeep = 0
            }
        }
    }
    return isKeep
}

func findPartion(_ p: [(Int, Int)], _ x: [(Int, Int)]) -> Bool {
    if p[0].0 == p[1].0 {
        // x가 같은 경우 y 사이에 파티션 확인
        // ex) (2, 1), (2, 3)
        return !(x.filter { $0 == ((p[0].0, p[0].1 + 1)) }.isEmpty)
    } else if p[0].1 == p[1].1 {
        // y가 같은 경우 x 사이에 파티션 확인
        // ex) (1, 3), (3, 3)
        return !(x.filter { $0 == ((p[0].0 + 1, p[0].1)) }.isEmpty)
    } else {
        // xy 둘다 다르면(대각선에 위치한 경우) 교차하여 확인
        // ex) (0, 1), (1, 0)
        // 이때, 두 군데 모두 파티션이 있어야 함 (&&연산자 사용)
        return !(x.filter { $0 == ((p[1].0, p[0].1)) }.isEmpty) && !(x.filter { $0 == ((p[0].0, p[1].1)) }.isEmpty)
    }
}
정확성테스트정확성테스트
테스트 1 〉통과 (0.74ms, 16.6MB)테스트 2 〉통과 (0.71ms, 16.7MB)
테스트 3 〉통과 (0.41ms, 16.6MB)테스트 4 〉통과 (0.45ms, 16.5MB)
테스트 5 〉통과 (0.42ms, 16.7MB)테스트 6 〉통과 (0.38ms, 16.6MB)
테스트 7 〉통과 (0.51ms, 16.5MB)테스트 8 〉통과 (0.46ms, 16.3MB)
테스트 9 〉통과 (0.40ms, 16.3MB)테스트 10 〉통과 (0.55ms, 16.7MB)
테스트 11 〉통과 (0.46ms, 16.6MB)테스트 12 〉통과 (0.54ms, 16.5MB)
테스트 13 〉통과 (0.42ms, 16.7MB)테스트 14 〉통과 (0.35ms, 16.6MB)
테스트 15 〉통과 (0.39ms, 16.6MB)테스트 16 〉통과 (0.37ms, 16.7MB)
테스트 17 〉통과 (0.55ms, 16.6MB)테스트 18 〉통과 (0.60ms, 16.6MB)
테스트 19 〉통과 (0.51ms, 16.5MB)테스트 20 〉통과 (0.71ms, 16.5MB)
테스트 21 〉통과 (0.82ms, 16.6MB)테스트 22 〉통과 (0.41ms, 16.5MB)
테스트 23 〉통과 (0.27ms, 16.5MB)테스트 24 〉통과 (2.96ms, 16.6MB)
테스트 25 〉통과 (0.23ms, 16.5MB)테스트 26 〉통과 (0.24ms, 16.5MB)
테스트 27 〉통과 (0.40ms, 16.5MB)테스트 28 〉통과 (0.41ms, 16.4MB)
테스트 29 〉통과 (0.36ms, 16.6MB)테스트 30 〉통과 (0.32ms, 16.6MB)

다른 사람의 풀이

func isManhattanDistance(_ places:[[String]]) -> Bool {
    // (1, 0), (2, 0), (0, 1), (0, 2), (1, 1), (-1, 1)
    let dx = [ 1, 2, 0, 0, 1, -1]
    let dy = [0, 0, 1, 2, 1, 1]
    for x in places {
        print(x)
    }
    for row in 0..<5 {      // 행 5개
        for col in 0..<5 {  // 열 5개
            if places[row][col] == "P" {    // 응시자인 경우
                for i in 0..<6 {
                    let (nx, ny) = (row+dx[i], col+dy[i])
                    
                    // 맨해튼 거리가 2이하인 곳에 다른 응시자(P)가 있을 때
                    if (0..<5).contains(nx) && (0..<5).contains(ny) && places[nx][ny] == "P" {
                        
                        if row == nx {          // 같은 행에 다른 응시자가 있을 때
                            if ny - col == 0 {  // 바로 옆에 있을 때
                                return false
                            } else {            // 한 칸 떨어져 있을 때
                                if places[row][col+1] != "X" {
                                    return false
                                }
                            }
                            
                        } else if col == ny {   // 같은 열에 다른 응시자가 있을 때
                            if nx - row == 0 {  // 바로 옆에 있을 때
                                return false
                            } else {            // 한 칸 떨어져 있을 때
                                if places[row+1][col] != "X" {
                                    return false
                                }
                            }
                        } else {    // 대각선에 다른 응시자가 있을 때
                            if row > nx {
                                if places[row-1][col] != "X" || places[row][col+1] != "X"{
                                    return false
                                }
                            } else {
                                if places[row+1][col] != "X" || places[row][col+1] != "X"{
                                    return false
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    return true
}

func solution(_ places:[[String]]) -> [Int] {
    
    // places를 [[[String]]] 형태로 만들기
    // ex) [[["P", "O", "O", "O", "P"], ["O", "X", "X", "O", "X"], ...]]
    let places = places.map {$0.map{$0.map{String($0)}}}
    var res:[Int] = []
    
    for place in places {
        // 대기실 별로 거리두기 확인하기
        res.append(isManhattanDistance(place) ? 1:0)
    }
    
    return res
}

dx와 dy는 아래 그림 처럼 P(0, 0)을 기준으로 맨해튼 거리가 2 이하인 곳에 또 다른 응시자(P)가 있는지 확인하기 위한 x, y좌표를 미리 만들어둔 것이다.

// (1, 0), (2, 0), (0, 1), (0, 2), (1, 1), (-1, 1)
let dx = [ 1, 2, 0, 0, 1, -1]
let dy = [0, 0, 1, 2, 1, 1]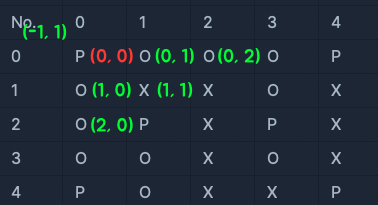

정확성테스트정확성테스트
테스트 1 〉통과 (0.22ms, 16.4MB)테스트 2 〉통과 (0.33ms, 16.4MB)
테스트 3 〉통과 (0.21ms, 16.6MB)테스트 4 〉통과 (0.19ms, 16.6MB)
테스트 5 〉통과 (0.19ms, 16.5MB)테스트 6 〉통과 (0.20ms, 16.5MB)
테스트 7 〉통과 (0.22ms, 16.4MB)테스트 8 〉통과 (0.21ms, 16.5MB)
테스트 9 〉통과 (0.19ms, 16.4MB)테스트 10 〉통과 (0.21ms, 16.2MB)
테스트 11 〉통과 (0.34ms, 16.4MB)테스트 12 〉통과 (0.34ms, 16.4MB)
테스트 13 〉통과 (0.37ms, 16.5MB)테스트 14 〉통과 (0.21ms, 16.5MB)
테스트 15 〉통과 (0.19ms, 16.5MB)테스트 16 〉통과 (0.20ms, 16.4MB)
테스트 17 〉통과 (0.21ms, 16.4MB)테스트 18 〉통과 (0.21ms, 16.6MB)
테스트 19 〉통과 (0.21ms, 16.6MB)테스트 20 〉통과 (0.20ms, 16.7MB)
테스트 21 〉통과 (0.21ms, 16.6MB)테스트 22 〉통과 (0.19ms, 16.3MB)
테스트 23 〉통과 (0.21ms, 16.4MB)테스트 24 〉통과 (0.27ms, 16.4MB)
테스트 25 〉통과 (0.20ms, 16.4MB)테스트 26 〉통과 (0.18ms, 16.6MB)
테스트 27 〉통과 (0.19ms, 16.6MB)테스트 28 〉통과 (0.20ms, 16.7MB)
테스트 29 〉통과 (0.30ms, 16.6MB)테스트 30 〉통과 (0.21ms, 16.4MB)

정리

⏰
목표 풀이 시간 : 1시간
실제 풀이 시간 : 3시간 46분

이 문제는 2021년 카카오의 여름 인턴십을 위해 출제된 문제로 총 5문제 중 두 번째로 출제되었다.

해설

참고
주어진 5×5 크기의 대기실을 다음과 같은 그래프로 볼 수 있습니다.

  • 하나의 칸을 정점으로 봅니다.
  • 모든 칸에는 상하좌우 인접한 칸으로의 간선이 있습니다.
  • 단, 파티션이 있는 칸에서 나오거나 파티션이 있는 칸으로 들어가는 간선은 없습니다.

그러면 이 문제는 사람이 있는 정점에서 거리 2 이내에 다른 사람이 있는 정점이 있는지를 검사하는 그래프 탐색 문제로 볼 수 있습니다.

따라서 사람이 있는 정점들에서 시작하는 깊이 우선 탐색(DFS) 또는 너비 우선 탐색(BFS) 알고리즘을 사용하면 해결이 가능합니다. 이때, 거리 2 이내만 확인하면 된다는 점에 유의하여 구현해야 합니다.

이 방법 이외에도, 거리 2 이내까지만 확인하면 문제를 풀 수 있기 때문에 이중 반복문을 사용해서 직접 한 칸씩 확인하는 것도 충분히 가능한 방법입니다.

후기

프로그래머스 질문하기에서 DFS로 풀었다는 내용이 많아서 DFS가 뭐지 싶었는데, 정보처리기사 공부할 때 배웠던 깊이 우선 탐색이었다.

해설에도 나와있듯이 깊이 우선 탐색 또는 너비 우선 탐색 알고리즘을 이용해 풀 수 있는 문제였다.

나는 이중 반복문으로 일일이 확인하여 풀었는데, 확실히 다른 사람의 풀이가 더 깔끔하다. (탭 단계가 깊긴 하지만)

문제를 풀긴 풀었지만 총 시험 시간(4시간)을 한 문제에 할애한 셈이다..🥲 분발하자..!🔥

profile
Minji Kim
iOS Developer
이전 포스트

[Swift | 프로그래머스 Lv.2] [1차] 뉴스 클러스터링 (2018 KAKAO BLIND RECRUITMENT)

다음 포스트

[Swift | 프로그래머스 Lv.2] 튜플 (2019 카카오 개발자 겨울 인턴십)

1개의 댓글

comment-user-thumbnail
Henry
2023년 8월 13일

다른사람의 풀이에서 (-1, 1)의 좌표가 잘못 나온것 같아요! 오른쪽 위를 나타내는게 아닌가 싶습니당

답글 달기