
오늘의 주제는 '완전탐색'
[최소 직사각형]
문제

입력과 출력
코드
def solution(sizes):
#가장 큰수들의 최댓값
#가장 작은 수들의 최댓값
width=[]
length=[]
for i in range(len(sizes)):
if sizes[i][0]>sizes[i][1]:
temp=sizes[i][0]
sizes[i][0]=sizes[i][1]
sizes[i][1]=temp
width.append(sizes[i][0])
length.append(sizes[i][1])
answer=max(width)*max(length)
return answer알고리즘
명함을 넣을 수 있는 가장 작은 지갑의 크기를 계산해야 한다.
단순히 가장 큰수들의 최댓값과 가장 작은 수들의 최댓값을 곱하면 나온다고 생각했지만
가로 세로가 매칭되어 있기 때문에 이 점을 고려해야한다.
따라서 가로 세로를 비교하여 작은 수를 왼쪽으로 옮겨주고, 큰 수는 오른쪽에만 남게 구성한다.
그리고 sizes[i][0]을 width 배열에 담아주고
sizes[i][1]을 length 배열에 담아준다.
각각의 배열에서 최댓값을 추출하여 곱해주면 답이 된다.

문제를 이해하는 데 조금 오래걸렸다.
갈피를 잡지 못할때 검색을 해서 힌트를 얻었고, 단순히 '가장 작은 수들의 최댓값과 가장 큰 수들의 최댓값을 찾아 곱하자'라고 생각해서 처음 짠 코드는
def solution(sizes):
#가장 큰수들의 최댓값
#가장 작은 수들의 최댓값
arr=[]
for i in range(len(sizes)):
arr.append(sizes[i][0])
arr.append(sizes[i][1])
arr.sort()
arr_b=arr[0:len(arr)//2]
arr_a=arr[len(arr)//2:len(arr)]
answer=arr_b[-1]*arr_a[-1]
return answer이 코드였다..!
통과되는 듯 하였으나
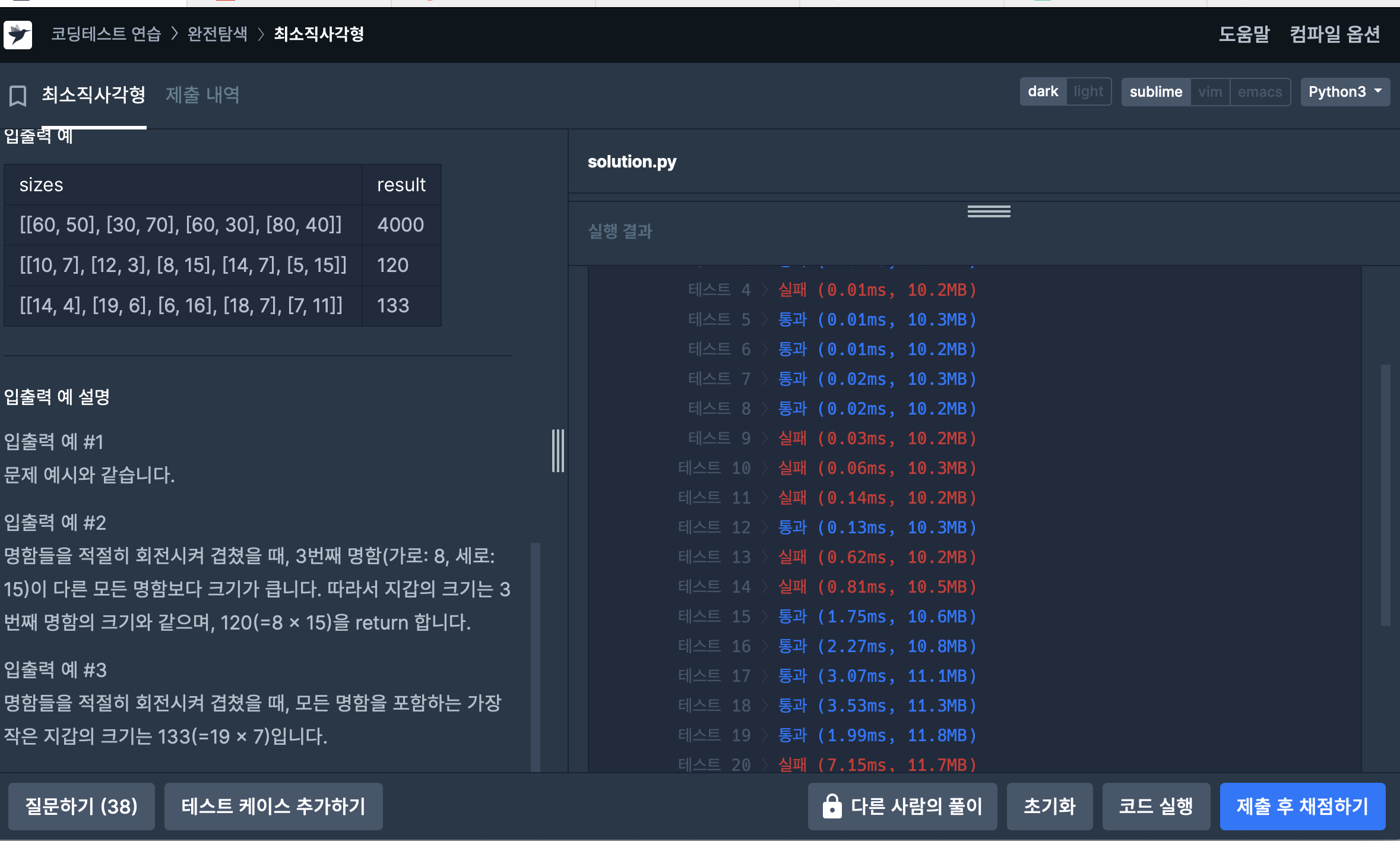
특정 케이스들에서 실패하여
요리조리 살펴보고 생각해 본 결과...
가로 세로가 매칭되어있는데 이 배열을 한꺼번에 정렬하고 작은수 중 최댓값 큰 수중 최댓값을 고르면...! 안되겠구나...!
이 두값다 한쪽 변으로 쏠려있다면...? 문제가 있구나 드디어 깨달았다 ㅎㅎ..

그래서 다시 생각해보던 중, 그러면 두 변중에 작은수 큰수를 구분해주면 되지않을까...?!해서 (여기까지 생각이 닿는 시간은 2시간이었다..)
그러나
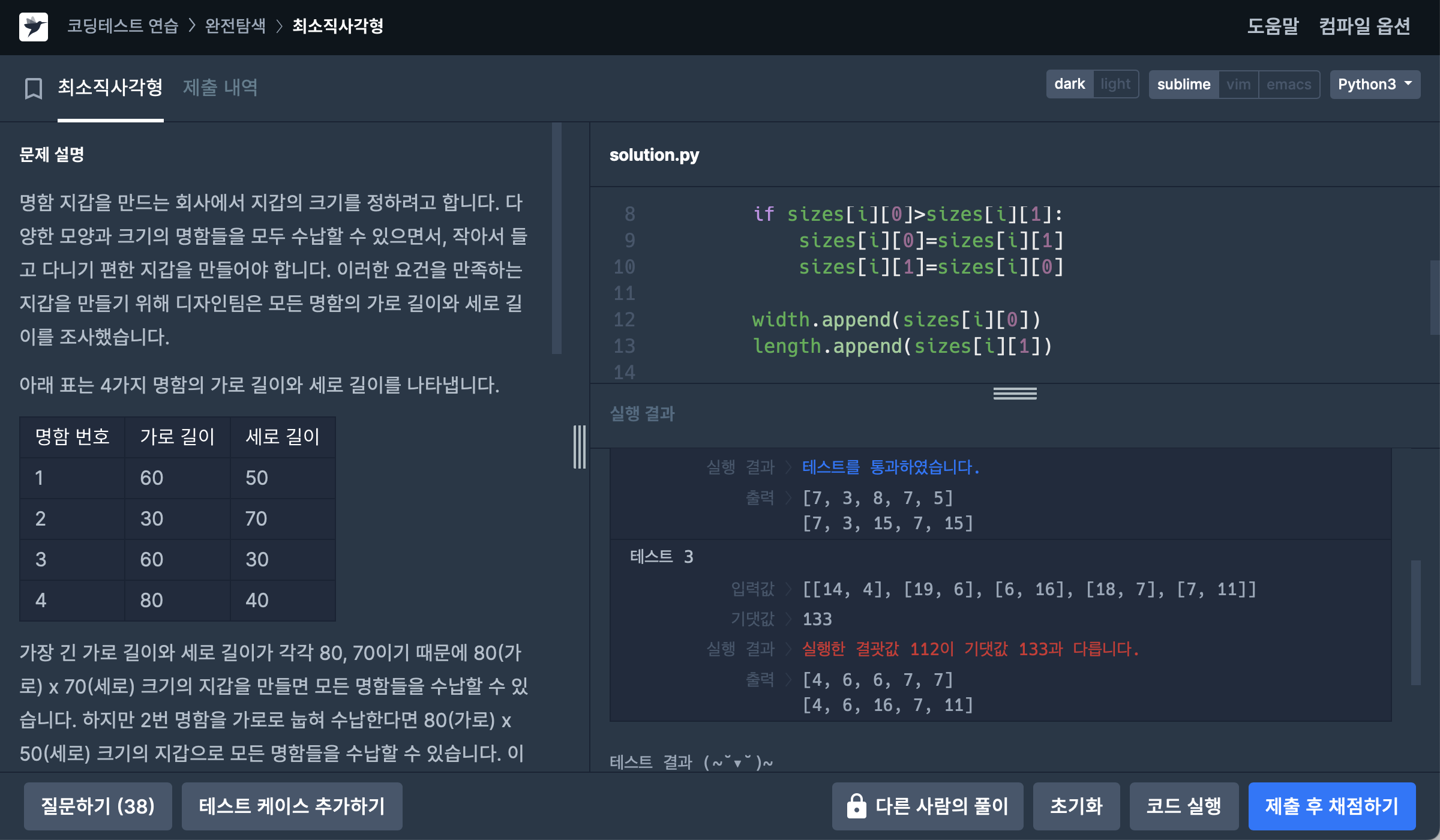
또 뭐가 문제야 ㅜㅜㅜ 싶어서 print해서 배열들의 출력을 보니.. 또다시 바보가튼 나...
두 변을 바꿔주는데, 다른 변수에 담지 않고 바꿔준게 문제였다 ㅎ
그래도 바로 알아차린 나.. 칭찬해..!
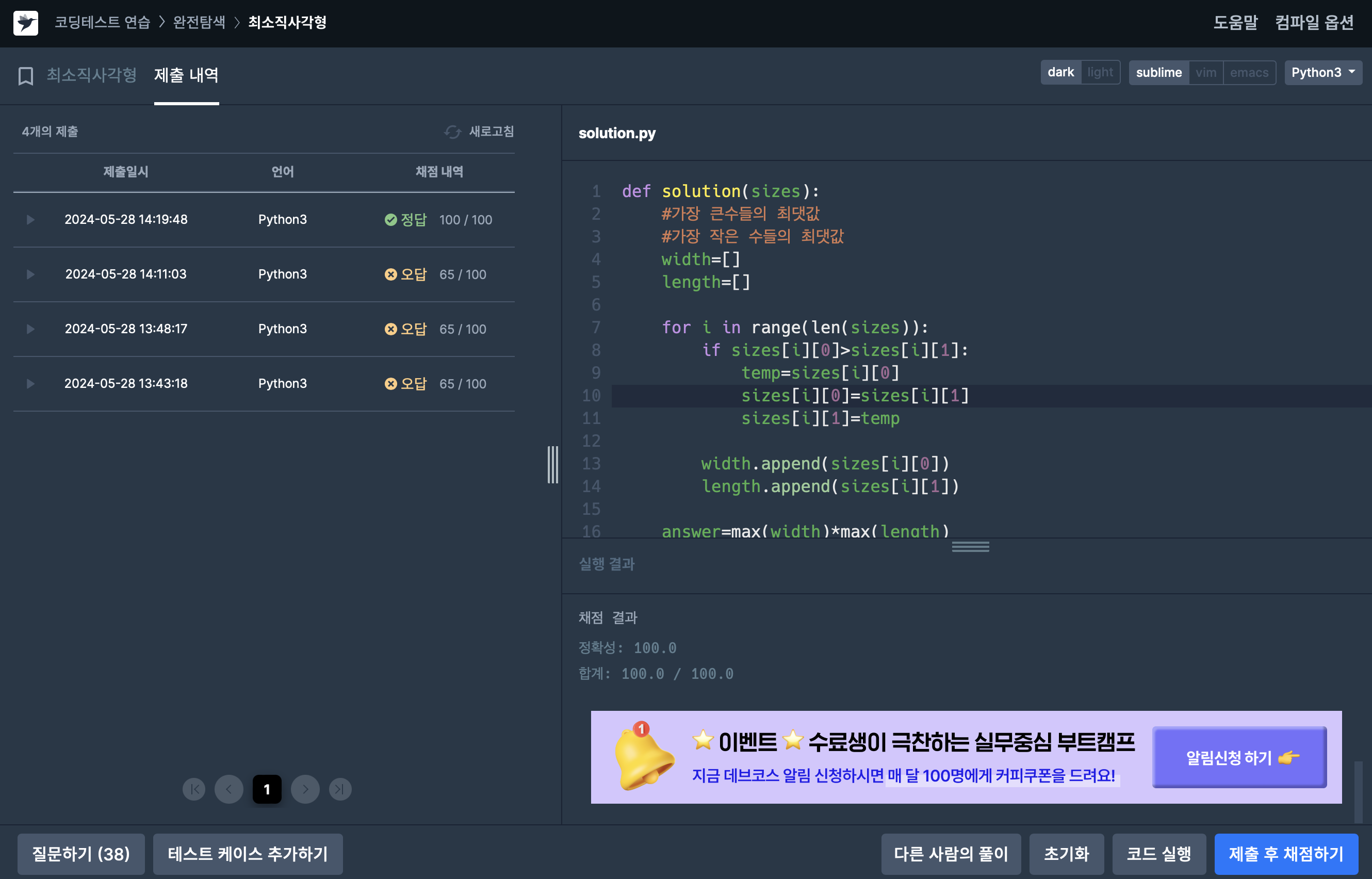
드디어 성공이다..!!!
Something new I learned
- 바로 코딩을 시작하기 전에 문제를 이해하는 시간을 좀 더 가져야할 것 같다..! 이번 문제는 코딩 실력보다는 문제 이해가 부족햇다,,
- 완전탐색
To do List
- 완전탐색 알고리즘
- 시간 복잡도
이번 주말에는 이 두 개념을 공부해서 정리해볼까 한다..
