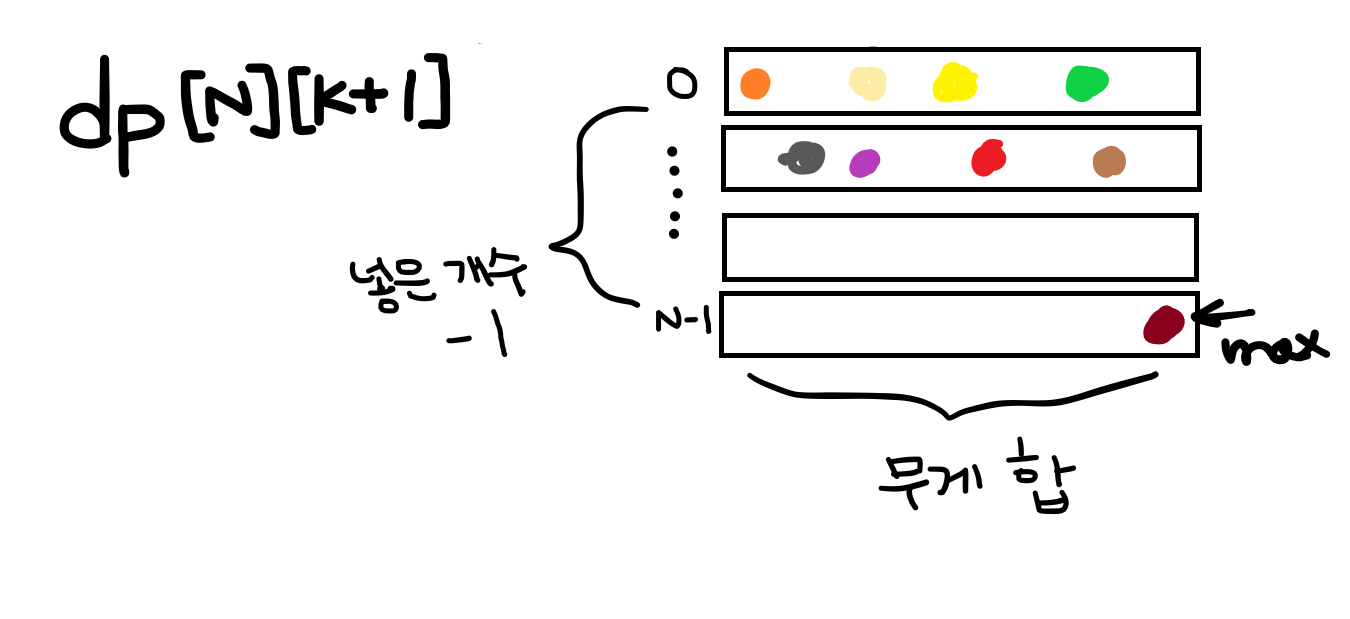
Knapsack 알고리즘
Fraction 냅색 알고리즘
분할이 가능한 경우 그리디 알고리즘으로 풀 수 있다.
배낭에 담을 수 있는 용량이 있으면, A,B,C 물건 중 무게 당 가치가 순서로 정렬을 한다.
가치가 큰 물건부터 넣고 남은 용량은 잘라서 담아주면 된다.
| a | b | c | |
|---|---|---|---|
| 무게 | 2 | 5 | 3 |
| 가치 | 10 | 20 | 30 |
| 무게 당 가치 | 5 | 4 | 10 |
Q . 총 가방의 용량이 8일 때 최대 가치는?
A . 무게당 가치가 높은 순서가 c > a > b 이므로 c와a를 먼저 담고, 남은 1만큼의 무게를 c/3으로 채워주면 된다.
0/1 냅색 알고리즘
분할이 불가능 한 경우 DP 알고리즘으로 풀 수 있다.
0/1 은 물건을 포함하거나 포함하지 않거나의 의미이다.
무게와 가치라고 했을 때
1. 가치 높은 순으로 넣어보거나
2. 무게 낮은 순으로 넣어보기 해도 반례가 있기 때문에!
개수가 n개가 들어오면, 포함/미포함 * 포함/미포함 ... 포함/미포함의 경우의수를 모두 알아봐야 한다.
n개의 모든 부분 집합의 개수 (2n)만큼 탐색해야 한다
재귀 DP 설계
- 포함하는 경우:
현재물건의 가치 + dfs(개수+1, 현재 물건의 무게)- 지금까지의 무게와 현재물건의 무게의 합이 용량보다 작을 때만 포함한다.
- 포함하지 않는 경우:
가치0 + dfs(개수+1, 무게0) - return값: Math.max(포함하는경우의 가치, 포함하지 않는 경우의 가치)
- 종료 조건: 현재물건의 인덱스가 개수n과 같다.
백준 평범한 배낭 문제 풀이
import java.io.*;
import java.util.Arrays;
import java.util.Comparator;
import java.util.stream.Stream;
//230122
public class Main{
static int[][] dp;
static int N;
static int K;
static int[] W;
static int[] v;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] line = br.readLine().split(" ");
N = Integer.parseInt(line[0]); // 개수
K = Integer.parseInt(line[1]); //무게
int result = 0; // 출력: 가치최대
dp = new int[N][K+1];
W = new int[N];
v = new int[N];
for(int i =0;i<N;i++) {
String[] str = br.readLine().split(" ");
W[i] = Integer.parseInt(str[0]);//무게
v[i] = Integer.parseInt(str[1]);//가치
}
System.out.println(search(0,0));
}
private static int search(int i, int w){ //현재 몇번째 인지 , 지금 무게 얼만지
if(i == N) return 0; //더이상 개수를 담을 수 없으면 0을 더한다
if(dp[i][w] > 0) return dp[i][w]; //이미 탐색했으면 탐색한거 반환
int n1 = 0;
//포함
if(W[i] + w <= K){
n1 = v[i] + search(i+1,W[i] + w); 현 가치를 더해준다
}
//미포함
int n2 = 0 + search(i+1,w);
return dp[i][w] = Math.max(n1,n2);
}
}