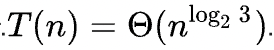Karatsuba Algorithm
- divide and conquer 개념을 적용하여 곱셈의 시간복잡도를 낮춘 알고리즘
일반적으로 n자리 수 곱셈의 시간복잡도는 O(N^2)이다.
코드만 봐도 이중 for문을 쓰고 있음을 알 수 있다.
Karatsuba Algorithm을 사용하면 시간복잡도를 N의 로그 승까지 빠르게 할 수 있다.
알고리즘
다음과 같은 두 수 n-digits의 x,y가 있고, 다음과 같이 분해하여 쓸 수 있다.
B는 2진수이면 2, 10진수이면 10이 들어갈 수 있다.
또한 m은 n보다 작은 양수이다.
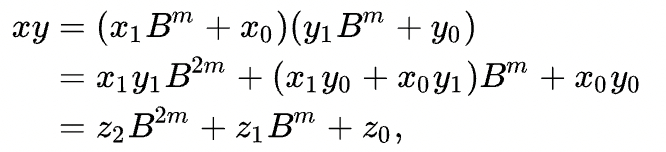
위에 나와있는 z0, z1, z2를 구하는 공식은 다음과 같다.
이 공식은 4번의 곱셈이 필요하다.
그러나 다음과 같이 z1의 식을 덧셈으로 바꾸면 3번의 곱셈으로 해결할 수 있다.
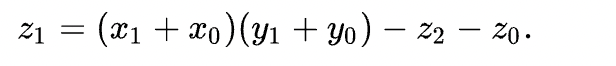
예시
먼저 12345와 6789를 다음과 같이 적는다.
B=10, m=3이다.
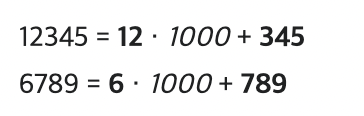
그리고 아래와 같이 z2, z0, z1을 순서대로 구한다.
결과값은 m 오른쪽 시프트를 사용한 값을 곱해줘서 만들 수 있다.
시간복잡도
이 알고리즘에서 발생하는 곱셈, 뺄셈, 시프트 연산은 n에 비례하므로 n이 증가함에 따라 비용을 무시할 수 있다.
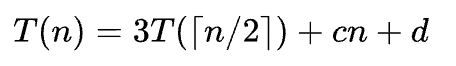
위와 같은 식에 따라서 총 시간복잡도는 다음과 같다.
참고
Game Programmer