Min-max tree는 경우의 수가 많은 게임에서 실제 적용이 어렵다
많은 수를 내다보아야 하는데,
Depth에 따라 move에 수가 빠르게 증가하고
컴퓨터 연산에 한계로 인해 깊게 탐색하기 어려운 경우가 존재한다
특히 실시간성을 요구하거나 시간제약이 있는 경우 Min-max tree를 사용하기에는 더욱 어렵다
이럴 때 Monte-Carlo Tree Search은 Min-max tree의 단점을 보완하고 있다
Monte-Carlo Tree Search 특징
- Bandit-based method
- UCB 수식을 트리에 적용한 UCT값을 사용한다
- Min-max와 달리 모든 노드를 확장하지 않고 정해진 개수만큼만 확장하고 이 중 best를 찾는다
- 이전에 탐색하면서 생긴 reward를 누적해서 그 reward를 최대화한다 (UCT값 이용)
- 휴리스틱을 사용하지 않는다
- 휴리스틱을 사용하지 않고 랜덤 시뮬레이션을 통해 얻은 값을 기반으로 탐색을 진행한다
- 따라서 게임에 대한 사전 지식이 없어도 금방 적용할 수 있다
- 언제라도 탐색을 중단할 수 있다
- simulation 중에 시간 제약에 걸린다면 그 즉시 탐색을 멈추고
탐색한 부분까지의 리워드를 반환할 수 있다
- Exploration과 Exploitation의 밸런스가 잘 맞는다
- Exploration: 아직 탐색되지 못한 쪽의 트리를 탐색할 기회를 주는 것
- Exploitation: 좋은 UCT값을 가진 쪽의 트리를 계속 더 탐색하는 것
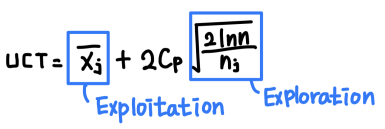
- Cp는 두 값 사이의 밸런스를 조정할 수 있는 상수
- n은 부모 노드의 방문 횟수
- nj는 해당 노드의 방문 횟수
- Xj의 평균은 해당 노드의 누적된 reward의 평균값
Monte-Carlo Tree Search Algorithm
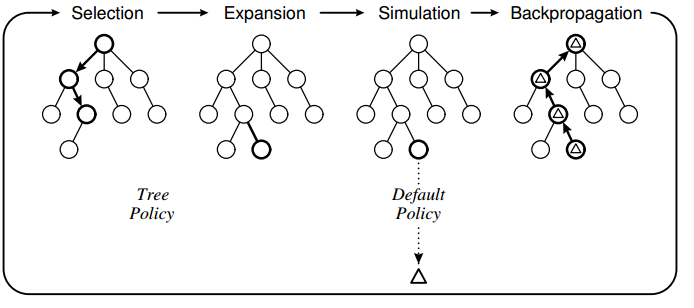
-
Selection
- 여러 후계노드들 중 UCT값이 좋은 쪽의 노드를 탐색 노드로 결정한다 -
Expansion
- Tree policy에 따라 1개 혹은 그 이상의 후계노드를 만들어 트리를 확장한다 -
Simulation
- 후계노드들 중 첫번째 자식 노드를 탐색한다
- default policy를 따라 게임을 진행하여 reward를 얻는다 -
Backpropagation
- 얻은 reward를 부모에게 노드들에게 반영시킨다
이 때 partial tree의 역할이 중요한데,
처음에 partial tree가 없는 상태에서 시작하면 어느 정도 기본적 tree를 갖추기 위해 위 단계를 많이 진행해야 한다
그러나 partial tree가 build된 상태에서 시작하게 되면
불필요한 단계의 반복을 줄일 수 있고 자원도 덜 사용하게 된다
즉 몇 번 반복만으로도 각 노드의 값을 많이 채울 수 있다
Tree policy와 Default policy
- Tree policy
- leaf node를 selection하고 expansion하는 과정에 영향을 준다
- Exploitation과 Exploration의 밸런스를 맞추기 위해 Bandit-based method를 사용한다 - Default policy
- Simulation 단계에 영향을 준다
게임 후반에는 휴리스틱이 생겨서 Selection 전략에 변화가 생긴다
1. Max - 나의 이익을 최대로 하는 노드 선택
2. Robust - 방문횟수를 신뢰의 기준으로 삼아 방문횟수가 많은 노드를 선택
3. Max-Robust - 혼합 (보통 많이 쓰임)
