수업 필기를 목적으로 작성했기 때문에 해석하기 많이 어렵습니다..

Equivalence relations

각 집합에 파티션으로 구분이 되어있으면

THM 1)

Let Q be a partition of a set X. Define xRy to mean that for some set S in Q, both x and y belong to Q. Then R is reflexive, symmetric, transitive.

각 파티션는 reflexive, symmetric, transitive 하다.

ex)

Consider the partition Q={{1,3,5}, {2,6}, {4}} of X={1,2,3,4,5,6}.
The complete relation R is ={(1,1)(1,3)(1,5) (3,1)(3,3)(3,5) (5,1)(5,3)(5,5)
(2,2)(2,6)(6,2)(6,6) (4,4)}

THM 2)

THM 2) Let X be a set and R a relation on X, R is an equivalence relation on
X ↔ R is reflexive, symmetric and transitive.

X에 대한 relation R이 equivalence relation 이라는 것은 R이 reflexive, symmetric, transitive 하다는 것.

ex) Let X= S5, R= {(1,1)(1,3)(1,5)(2,2)(2,4)(3,1)(3,3) (3,5)(4,2) (4,4) (5,1)(5,3) (5,5)} E.R?

ex28) R={(a,a)(b,c)(c,b)(d,d)} on X= {a,b,c,d} ER?
(sol) (c,c) !$\in$R, (b,c) (c,b) → (b,b) !$\in$ R

not reflex not transit

set of equivalence classes (동치류)

모든 원소에 대해서

[a] (세트 a) 라는 것은 a와 관련된 모든 원소의 집합이다.

그러므로 S 는 모든 X의 원소 a에 대하여 [a]의 집합이다.

S를 X의 파티션이라고도 한다.

• X의 모든 원소들은 적어도 하나의 동치류에 속한다.

ex) Let R={(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)(2,2) (2,6)(6,2) (6,6)(4,4)}

[1] = [3] = [5] = {1, 3, 5}

[2] = [6] = {2, 6}

[4] = {4}

따라서 X는 3개의 동치류로 구성되어 있다.

S = [1] U [2] U [4] = {1,3,5} U {2, 6} U {4}

ex)

Let S={1,2,3,4,5,6}. For x,y $\in$ S. Let xRy if x-y is divisible by 2.
Show that R is an E.R. - Find E.C. relative to R.
(sol)
1) R is reflexive
2) R is SYM => since x-y / 2 이면 <=> y-x / 2 이기 때문에
3) Suppose, xRy and yRz, then there exist k and m, such that
x-y = 2k and y-z = 2m. // since it is divisible by 2
x-z = (x-y) + (y-z) = 2k+2m=2(k+m). so R is TRAN
4) by 1)2)3), it is E.R on S.
5) E.C:

[1] = {x$\in$S6: x-1 is divisible by 2} = {1,3,5}
[2] ={x$\in$S6: x-2 is divisible by 2} ={2,4,6}

Which leads to a natural partition of set S6 into [1] and [2], and [1]U[2] = S6.

equivalence classes 가 맞는지 증명

1) for all x $\in$ S, [x] ≠ 0 모든 동치류는 공집합이 아니다.

2) if [x] ≠ [y], then [x]$\cap$[y] = $\empty$ 모든 동치류끼리는 mutually disjoint

3)$\cup${[x] | x $\in$ S } = S 모든 동치류끼리 union 하면 집합이 된다.

Closure

Relation 은 reflesive, symmetric, transitive 의 성질을 가지고 있지 않을 수 있다.

이런 relation들을 그 성질을 갖도록 relation에 관련된 순서쌍을 첨가할 수 있다.

따라서 우리가 원하는 성실을 가지며 관계 R을 포함하는 최소의 관계 R1을 찾는게 CLOSURE

1) reflexive closure

R1 = R $\cup$ $\nabla$ : R을 포함한 A에 대해 가장 작은 반사적 관계

R의 reflexive closure 는 R $\cup$ $\nabla$ 라고 표현한다.

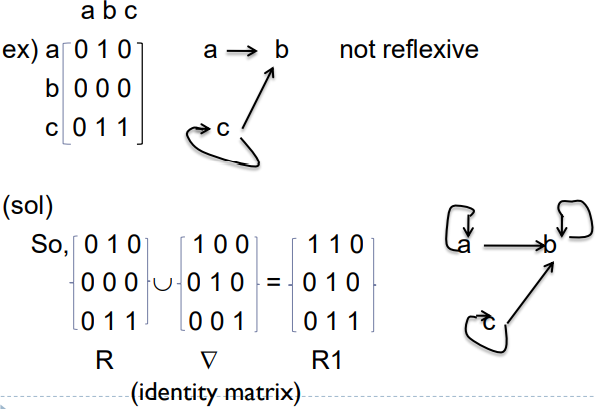
2) symmetric Closure

if $\exist$(x,y) $\in$ R, such that (y,x) !$\in$ R,

then R U $R^{-1}$

R U $R^{-1}$ is smallest symmetric closure containg R.

R에 (x,y) 가 있을 때 (y, x) 가 없다면 symmetric 관계가 아니므로

R의 역을 포함시키면 symmetric 관계가 된다.

따라서 $R \cup R^{-1}$ 은 R의 symmetric Closure 이다.

ex) A={a,b,c,d}. R={(a,b)(b,c)(a,c)(c,d)}
Then R-1 = {(b,a)(c b)(c a)(d c)}
so symmetric closure of R is
R $\cup$ R-1 = {(a b)(b c)(a c)(c d)(b a)(c b)(c a)(d c)}

3) Transitive Closure

R이 추이관계가 아닐 때

R* is transitive closure of R

transitive closure 을 구하기 위한 알고리즘이 있다.

Warshall's algorithm

그래프나 매트릭스를 이용해서 transitive closure 를 구하는 건 비효율적이다.

따라서 transitive closure를 찾기 위해 와셜 알고리즘을 사용한다.

알고리즘의 주장 : find $W_k$ from $W_{k-1}$

1. 오리지널 매트릭스의 1들을 다음 매트릭스에 덮어쓴다.

2. k 번째 열과 행의 원소들을 (p, q) 라고 하면 행은 p, 열은 q 이런식으로 표현해서 집합을 만들고 cartesian product를 한다.

   (p1, p2) x (q1, q2, q3) = (p1, q1) (1, 2) (1, 3) (2, 1) (2, 2) (2, 3)

이중에서 1인 부분만 쓴다.

1. nxn 매트릭스라면 n번 2. 를 반복한다.