해시 테이블

해시테이블은 해시 함수를 통해 O(1)의 시간 복잡도로 빠르게 데이터에 접근이 가능한 자료구조다. 리스트 자료구조와 비교했을 때 리스트는 O(N)의 시간 복잡도로 데이터를 찾는 반면 (문자열이면 O(NM)의 시간이 걸린다.) O(1)의 시간 복잡도로 데이터를 접근할 수 있다.
해시의 작동 원리는 해시 함수에서 알 수 있다.

해시 함수

• 해시함수: 임의의 값을 임의의 길이의 값으로 매핑하는 함수. 특정한 구간에서만 매핑이 되기 때문에 아무리 큰 데이터라도 정해진 구간에서 벗어나지 않는 값으로 매핑이 된다. (해시 함수나 bloom filter에서 사용된다.)

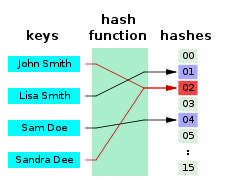
출처 [위키백과 - 해시]

따라서 위 사진처럼 (임의의 값) -(해시 함수)> (임의의 길이의 매핑된 값)으로 매핑한 후 그 값을 통해 데이터를 저장한 구역을 찾는다.

해시 충돌

하지만 아무리 큰 데이터도 정해진 구간에 벗어나지 않는 값으로 매핑된다는 뜻은 다른 데이터도 같은 값으로 매핑될 수 있다는 의미가 될 수 있다.
예를 들어 숫자 해시 함수가 있다고 가정했을 때 함수는 x가 입력으로 주어졌을 때 x % 10을 출력으로 내보낸다. 그러면 x가 2 이던 12 이던 2라는 같은 값으로 매핑이 된다.

이 문제를 "해시 충돌" 이라고 부른다.
위 사진에서 "John Smith"와 "Sandra Dee" 같은 경우다.

import java.util.*;
class HelloWorld {
    public static void main(String[] args) {
        HashMap<String, Integer> hashMap = new HashMap<>();
        hashMap.put("abc...", 2); // 충분히 긴 문자열
        hashMap.put("abc...", 3); // 충분히 긴 문자열
    }
}

만약 해시 충돌을 생각하지 않고 위와 같이 구현한다면 해시 충돌이 일어났음에도 개발자는 알아차리지 못할 수 있다. 아무리 큰 문자열이라도 정해진 구간을 벗어나지 않는 해시값으로 매핑이 되기 때문이다.

• 증명
  해시 충돌은 비둘기집 원리로 증명할 수 있다. 1에서 100까지 해시값으로 만드는 해시함수에 1에서 101까지 숫자를 넣는다고 했을 때 한 해시값에 2개 이상 매핑될 수 있다(해시충돌). 이를 증명하기 위해 귀류법을 사용한다. 한 해시값에 오직 한개의 숫자만 매핑이 된다. 그렇다면 해시값을 전부 더하면 100개다. 그러나 101개를 한 해시값에 오직 한개의 숫자만 매핑이 될 수 있다는 가정은 틀리다. 때문에 한 해시값에 2개 이상 매핑될 수 있다.

이를 해결하기 위해

• 개방 주소법: 다른 해시 값으로 이동해서 저장하는 방법
• 해시 체이닝: 하나의 해시 값에 Linked List 자료구조를 연결해서 저장하는 방법. 이 방법을 자주 사용한다.

를 이용한다.

해시체이닝

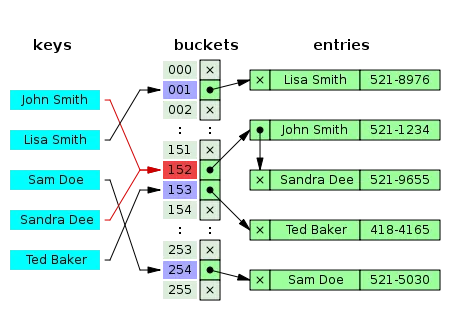
출처 [C++ 11 Hash Table, Hash Map, Dictionaries, Set, Iterators - Abu Obaida (Medium)]

같은 해시값을 가질 때는 위 사진처럼 버킷에 연결리스트 형태로 데이터를 저장한다.
하지만 연결리스트이기 때문에 만약의 경우 해시값이 편향되게 나오게 되었을 때 하나의 데이터를 찾는데 오랜 시간이 걸릴 수 있다.

HashMap<String, ArrayList<Object> hashMap = new HashMap<>();
...
if(!hashMap.containsKey(str)){
    hashMap.put(object, new ArrayList<>());
}    
hashMap.get(str).add(object);