Red Black Tree

Associate Container 중에 하나로 map이나 set 자료구조의 기반이 되는 Tree

기본적으로 Self Balancing Binary Search Tree이기 때문에 편향 트리로 구성될 일이 없으며, 때문에 검색, 삽입, 삭제의 시간복잡도가 O(logN)을 기록한다.

AVL 과의 차이

AVL과는 차이가 있다. 두 트리 다 Self Balancing Binary Search Tree라는 점은 같지만 AVL이 트리의 높이가 편향되는 것을 더 민감하게 체크한다.

예를들면 다음과 같은 트리는 RB 트리에서는 가능하지만 AVL Tree에서는 불가능하다.

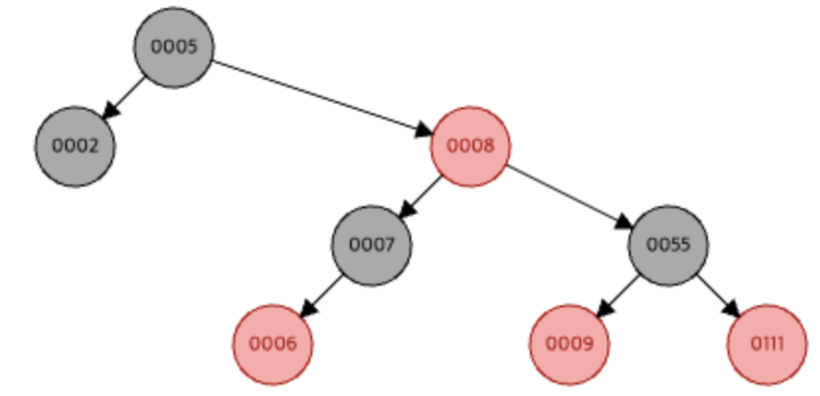
루트 노드의 입장에서는 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이는 2(Balance Factor)가 되어 AVL 트리에서는 Rotation이 일어나야하지만 RB 트리는 아래의 5가지 조건을 만족하기 때문에 가능하다.

5가지 조건

1. 노드의 색상은 빨강 혹은 검정이다.
2. 루트 노드는 검정이다.
3. 모든 리프노드는 검정이다.
4. 빨간 노드가 연달아 있을 순 없다.
5. 어떤 노드의 입장에서 모든 리프노드까지 경로의 검정 노드의 개수는 같다.

삽입

RB 트리는 삽입되는 노드는 무조건 빨강이어야 한다.

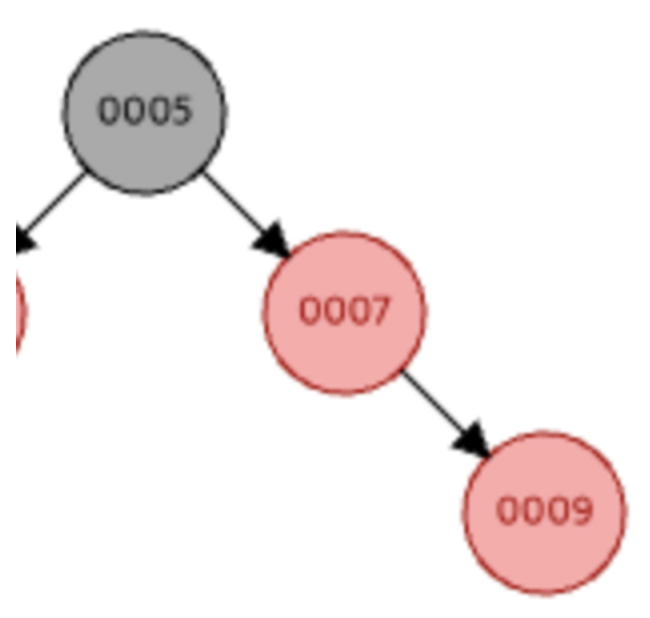
때문에 다음과 같이 삽입 될 수 있고 이는 4번을 위반한다. 4번을 지키기 위해 다음의 두가지 상황에 맞는 동작을 해야한다.

1. 삼촌 노드가 빨강일 경우 (Recoloring)

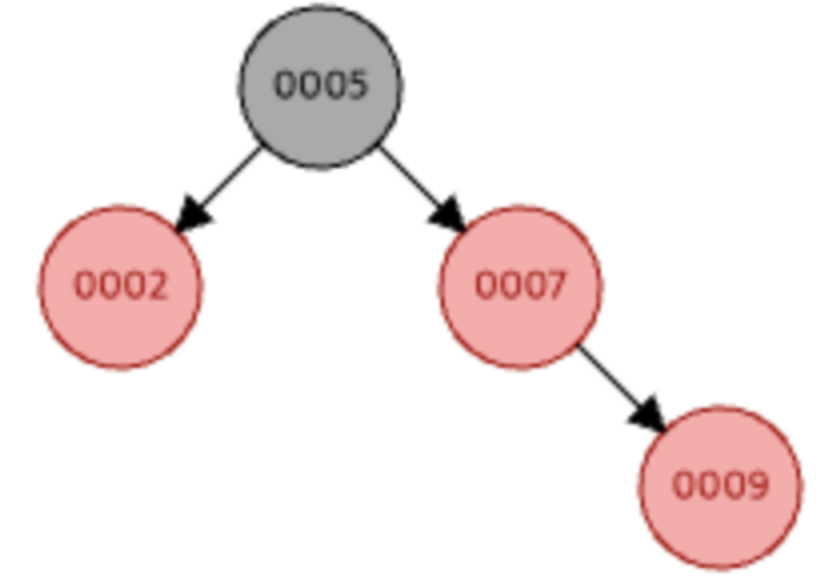
(삼촌 노드: 9번 노드의 입장에서 2번 노드는 삼촌 노드이다.)

삼촌 노드가 빨강일 경우는 삼촌과 부모 노드를 검정으로 다시 색칠해야한다. 그리고 조부모 노드는 빨강으로 색칠한다.

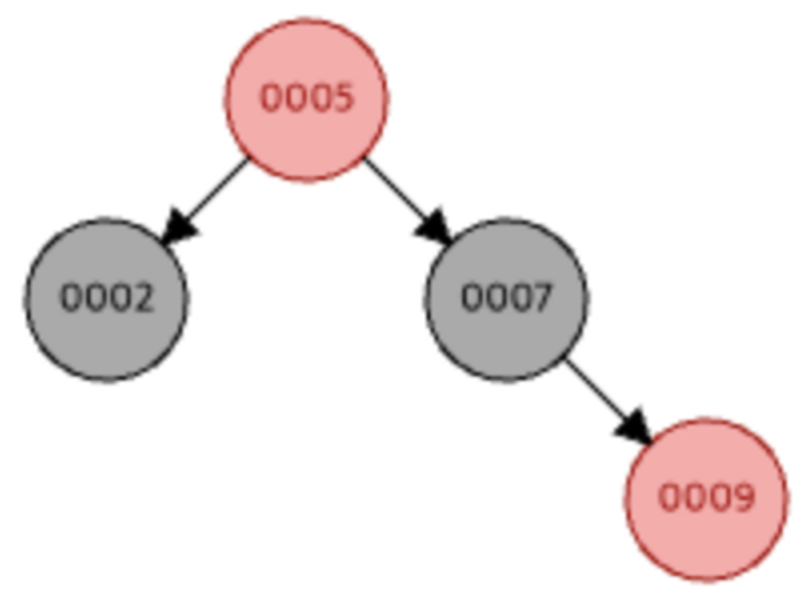
여기서 5번 노드는 루트 노드이기 때문에 2번 성질을 위반한다. (루트가 아닌 경우 그 노드부터 성질을 갖추는 지 재귀적으로 확인해야한다.)

따라서 5번 노드는 검정 노드가 된다.

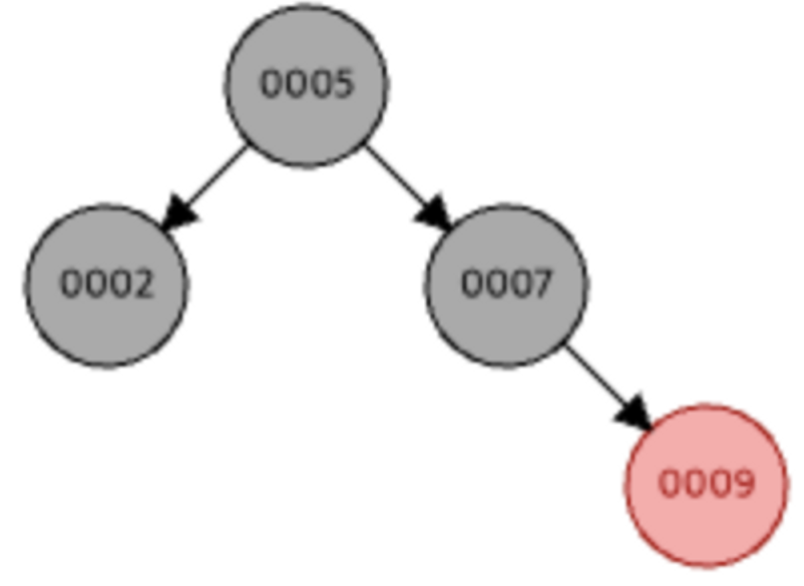
2. 삼촌 노드가 검정일 경우 (Restructuring)

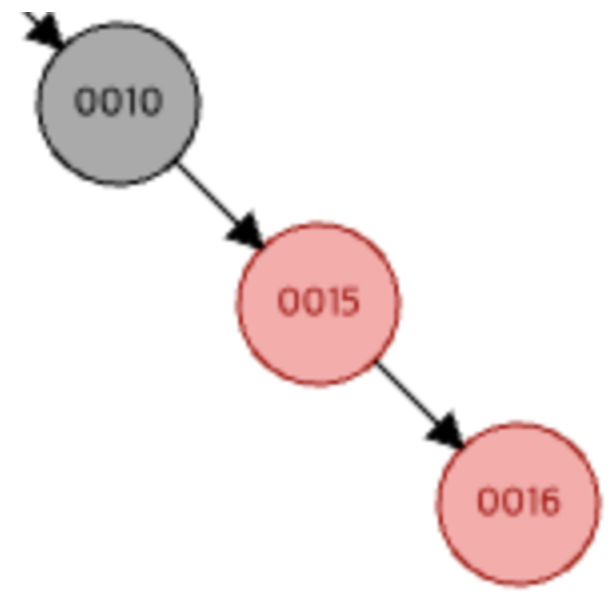
다음과 같은 경우가 삼촌 노드가 검정일 경우이다. 의아한건 16번 노드는 삼촌이 없는 것 같은데 왜 삼촌 노드가 검정이냐는 것이다.

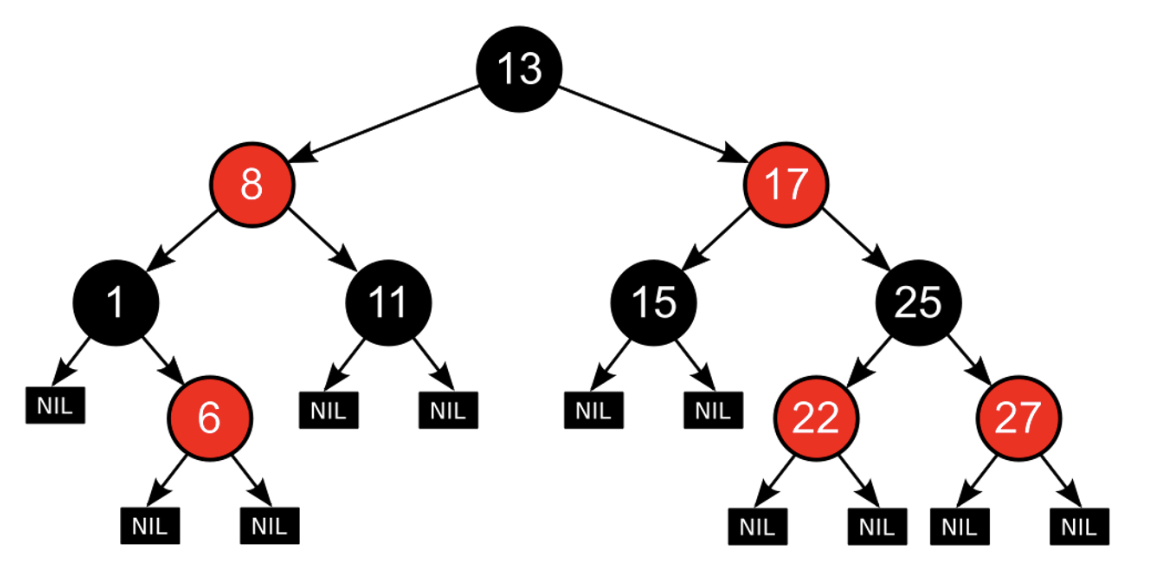[출처 - 위키피디아]

사실 3번 성질에 따라서 모든 리프 노드는 검정 노드이며 NIL이라고 불린다. 빨강 노드가 리프처럼 보여도 사실은 리프가 아니다.

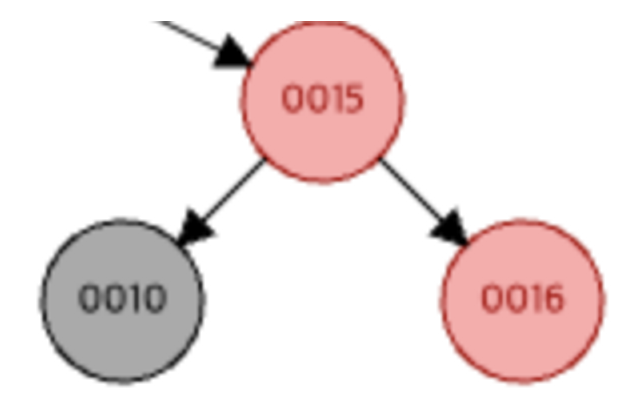
각설하고 계속 진행하면 rotation(restructuring)을 하면 다음과 같이 10번 노드와 그 자식들(NIL 혹은 다른 노드일 수 있다. ex: 10번 노드와 nil)이 15번 노드의 서브 트리가 된다.

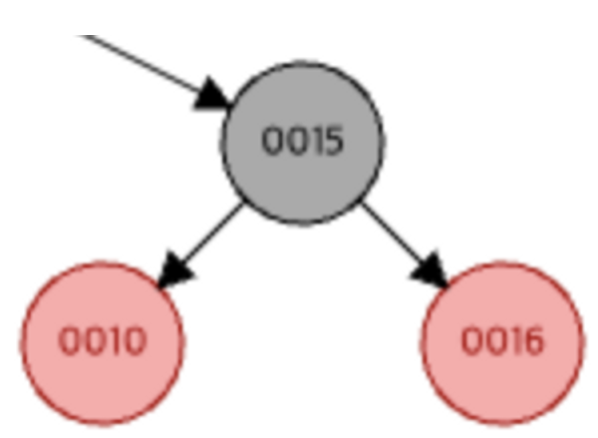
그 다음으로 15번 노드는 검정 노드로 바뀌고 그 자식들은 빨강 노드가 되면 4번 성질을 만족할 수 있다.

Restructuring은 Recoloring과 다르게 서브트리의 루트 노드가 검정 노드가 되면서 재귀적으로 4번을 만족하는지 확인할 필요가 없기 때문에 단 한번의 시퀀스 만으로도 가능하다.

삭제

삭제는 삽입과 다르게 6가지 case를 다루기 때문에 다음에 기회가 된다면 다뤄보도록 할 것이다.

RB Tree Deletion: https://medium.com/analytics-vidhya/deletion-in-red-black-rb-tree-92301e1474ea