FDF

Contents

---

• Subject

• 사전 지식

Subject

---

MANDATORY

MinilibX를 사용하여 주어진 map을 parsing하고, isometric projection을 이용하여 화면에 그리기.

BONUS

• zoom in, zoom out, shift
• rotate
• other projection.

사전 지식

---

MiniLibX

MiniLibX를 사용하여 화면에 나타내야 하기 떄문에, MiniLibX의 man 파일이 주어지는데, 그것을 우선으로 익혀야 한다.

MiniLibX 관련 포스팅
https://velog.io/@minjune8506/MiniLibX

---

isometric projection

isometric projection이란 등축투영법으로 3차원 물체를 2차원에 표현하기위한 투영법중에 하나이다. x, y, z 좌표축이 이루는 각도가 모두 같거나 120도를 이루는 특성을 지닌다.

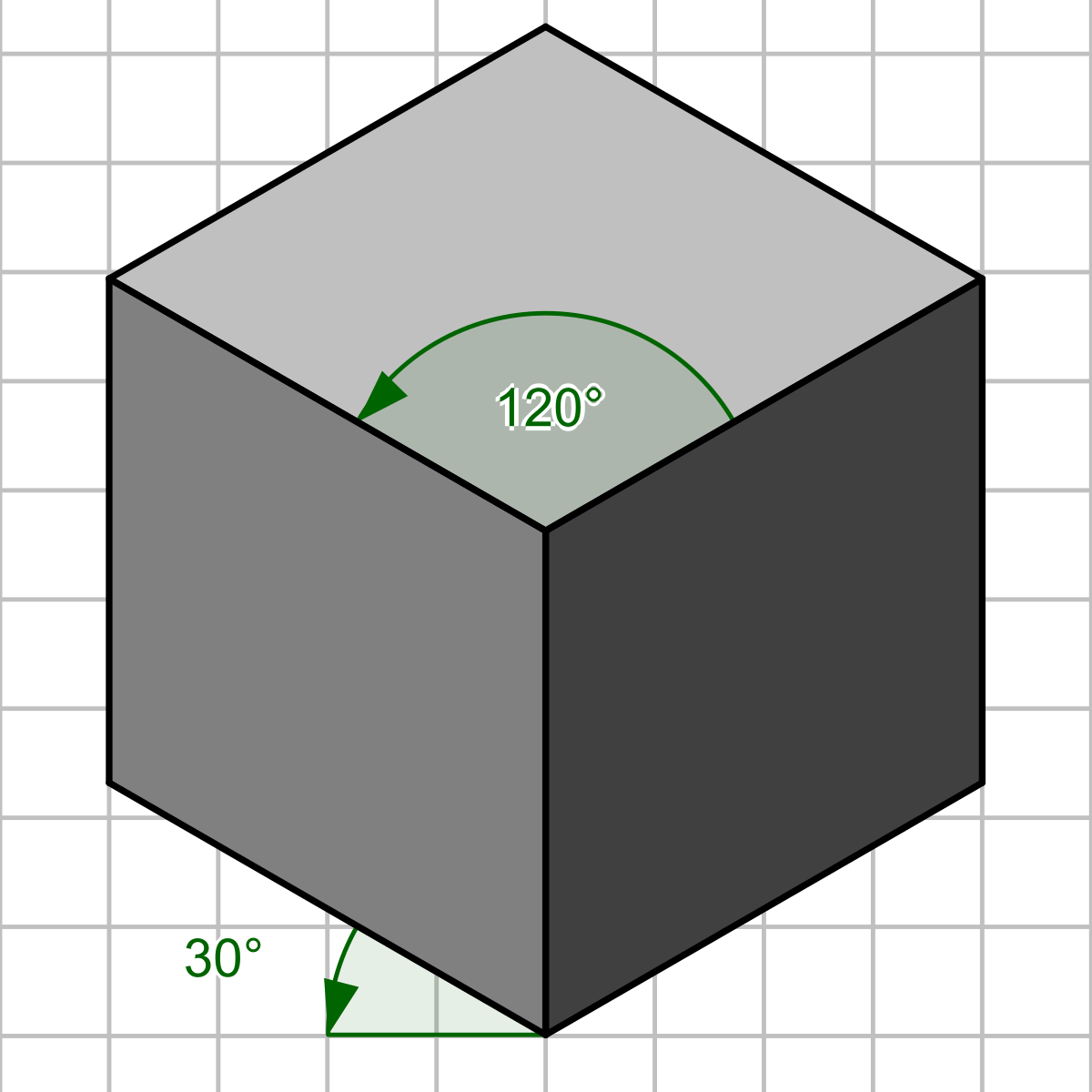출처 : 위키백과

이 그림과 같이 x, y 축을 30도씩 회전시켜 3차원 물체를 2차원으로 표현한 것이라고 보면 된다.

---

회전변환 행렬

2D

x' = x$\cos$($\theta$) - y$\sin$($\theta$)
y' = x$\sin$($\theta$) + y$\cos$($\theta$)

x. y축을 30도씩 돌리기 위하여 회전변환행렬을 사용하려고하는데, 2D에서 x' y' 의 좌표는 저 공식과 일치한다. 단위원의 반지름, $\cos$ $\sin$ 값과 삼각함수의 덧셈정리를 이용하여 공식을 유도 할 수 있다.

3D

x축을 기준으로 회전
x' = x
y' = y$\cos$($\theta$) - z$\sin$($\theta$)
z' = y$\sin$($\theta$) + z$\cos$($\theta$)

y축을 기준으로 회전
x' = x$\cos$($\theta$) + z$\sin$($\theta$)
y' = y
z' = -x$\sin$($\theta$) + z$\cos$($\theta$)

z축을 기준으로 회전
x' = x$\cos$($\theta$) - y$\sin$($\theta$)
y' = x$\sin$($\theta$) + y$\cos$($\theta$)
z' = z

2D에서의 회전 변환행렬을 3차원으로 확장한 행렬의 곱셈을 수행하면 위와 같이 정리 할 수 있다. 이 공식을 사용하여 축을 기준으로 회전을 할 것이고, 위의 2D 에서의 회전 행렬을 사용하여 축을 회전시켜 isometric projection을 구현할 것이다.
위의 공식을 유도할때 필요한 수학 지식들의 링크이다.

위키피디아 : 회전변환행렬
위키피디아 : 삼각함수의 덧셈정리
위키피디아 : 행렬 곱셈

직선을 그리는 알고리즘

직선을 그리는 알고리즘중에서 크게 2가지를 공부를 하였는데,
DDA 알고리즘과 Bresenham 알고리즘이다.
두 알고리즘 모두 직선을 그릴때 사용되는 알고리즘이지만, 어떤 계산방법을 쓰느냐에 따라서 달라지게 된다. DDA 에서는 실수형으로 계산을 하지만 Bresenham은 정수형으로 계산을 하게 된다.
따라서, Bresenham알고리즘이 훨씬 빠르며, 효율적으로 직선을 그릴 수 있다.
하지만 이 프로젝트를 진행하면서, 실수형 계산을 쓸 일이 많아서, 형변환 문제 떄문에 DDA 알고리즘을 선택하였다.

DDA Line Drawing Algorithm

 Algorithm DDA(x1, y1, x2, y2)
 {
    dx = x2 - x1
    dy = y2 - y1
    // dx는 x좌표의 차이, dy는 y좌표의 차이
    
    if (abs(dx) > abs(dy))
    	step = abs(dx)
    else
    	step = abs(dy)
    // dx > dy : 기울기가 1보다 작을경우
    // dx < dy : 기울기가 1보다 클 경우
    
    xinc = dx / step
    yinc = dy / step
    while (i <= step)
    {
    	put_pixel()
        x = x + xinc
        y = y + yinc
    }
 }

Bresenham's Line Drawing Algorithm

이 경우는 기울기가 1보다 작을 경우이며, 중단점 p를 이용해 찍고자하는 픽셀이 직선의 위에 있는지, 아래에 있는지를 판단한다.

Algorithm Bresenham(x1, y1, x2, y2)
{
   x = x1;
   y = y1;
   dx = x2 - x1
   dy = y2 - y1
   p = 2dy - dx
   while (x <= x2)
   {
   	put_pixel(x,y)
       x++
       if (p < 0)
       	p = p + 2dy
       else
      	{
       	p = p + 2dy - 2dx
           y++
	}
   }
}