이번 포스팅은 Neural Network를 빠르게 훈련시키는 최적화 알고리즘에 관한 내용입니다. 딥러닝은 크기가 큰 데이터의 경우 잘 작동하는데, 데이터의 크기가 클수록 훈련 속도는 느려집니다.
이런 경우 효율성을 높이기 위한 최적화 알고리즘을 잘 선택해야 합니다.
여러가지 최적화 알고리즘의 개념에 대해 알아보고 tensorflow 코드로 구현해 보았습니다.
1. Gradient Descent Algorithm (경사하강법)
Gradient Descent
경사 하강 법(Gradient Descent Algorithm)이란, 네트워크의 parameter들을 θ (->)라고 했을 때, Loss function 의 optima(Loss funtion의 최소화)를 찾기 위해 파라미터의 기울기(gradient) (즉, 와 )를 이용하는 방법입니다.
Gradient Descent에서는 에 대해 gradient의 반대 방향으로 일정 크기만큼 이동해내는 것을 반복하여 Loss function 의 값을 최소화하는 파라미터 를 찾습니다. 한 iteration에서의 변화 식은 다음과 같습니다.
Gradient Descent Algorithm
: learning rate
Gradient Descent Algorithm은 한 iteration에서 다룰 데이터 크기에 따라 세가지로 나눌 수 있습니다.
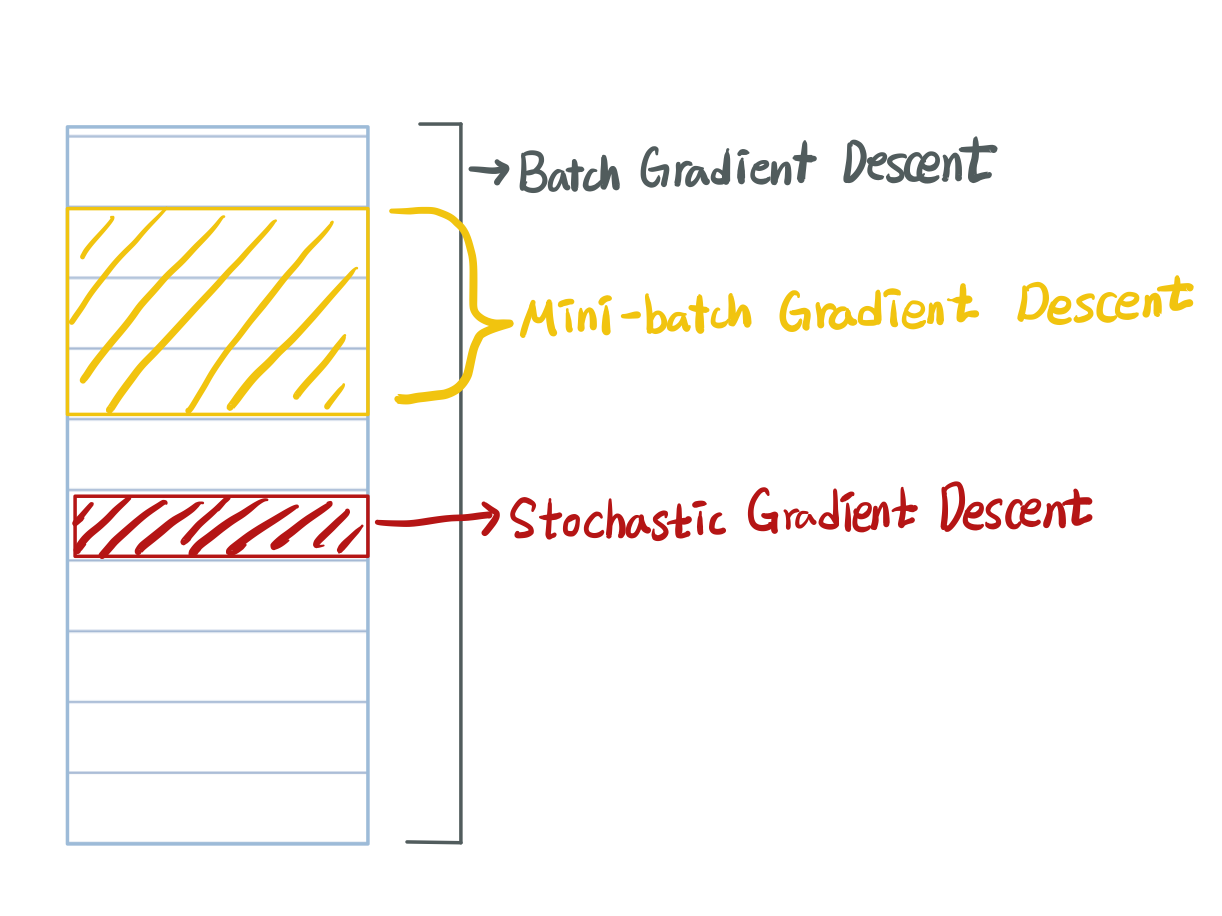
- Batch Gradient Desencet (BGD) :전체 데이터 셋에 대한 에러를 구한 뒤 기울기를 한번만 계산하여 모델의 parameter 를 업데이트 하는 방법
- Stochastic Gradient Descent (SGD) : 임의의 하나의 데이터에 대해서 에러를 구한 뒤 기울기를 계산하여, 모델의 parameter 를 업데이트 하는 방법
- Mini-batch Gradient Descent (MGD): 전체 데이터셋에서 뽑은 Mini-batch의 데이터에 대해서 각 데이터에 대한 기울기를 구한 뒤, 그것의 평균 기울기를 통해 모델의 parameter 를 업데이트 하는 방법
Mini-batch gradient desecent
앞서 말했듯이 Batch Gradient Descent (BGD)란, 학습 한 번에 모든 데이터셋에 대한 기울기를 구하는 것 입니다.
반면, Mini-batch Gradient Descent (MGD)란, 학습 한 번에 데이터셋의 일부에 대해서만 기울기를 구하는 것을 의미합니다. 즉 전체 데이터에 대한 기울기가 아닌, mini-batch로 나누어 기울기를 구하여 역전파하여 웨이트를 업데이트 하는 것 입니다.
만약 훈련데이터가 5,0000,000개가 있다고 가정해보겠습니다.
이때 min-batch의 크기를 1,000으로 잡는다면
...
으로 각 mini-batch set은 이고 각 mini-batch는 1000쌍의 x,y로 이루어지며, 총 mini-batch set은 5,000개가 됩니다.
이때 훈련은 다음과 같이 진행됩니다.

mini-batch의 데이터의 기울기를 모두 구하여 평균한 후, 가중치 업데이트를 진행합니다.
이 한 for문이 모두 돌았을 때, 즉 (전체 데이터 수)/(mini-batch size) = 5,000,000/1000 = 5,000번의 iteration이 완료되는 것이 1epoch입니다.
gradient를 묶어서 계산하기 때문에 BGD보다 훨씬 빠릅니다.
Understanding mini-batch gradient descent
gradient descent를 사용하기 위해서는 batch의 크기(mini-batch size)를 선택해야 합니다.
전체 데이터가 m개 일 때
- mini-batch size = m -> Batch Gradient Descent
- mini-batch size = 1 -> Stochastic Gradient Descent
- mini-batch size = n < m -> Mini-batch Gradient Descent

BGD는 전체 데이터에 대하여 오차를 계산하기 때문에 minimum에 안정적으로 수렴합니다. 하지만, 한 번의 iteration마다 모든 학습 데이터를 사용하므로 학습이 오래 걸립니다.
- 장점 : loss가 안정적으로 수렴 (cost function의 optimal로 안정적으로 수렴)
- 단점 : 한 iteration에 모든 데이터셋을 사용하기 때문에 학습이 오래 걸린다.
local optimal을 빠져나오기 힘들다.
SGD는 한번의 iteration마다 한개의 sample로 gradient descent하는 것이기 때문에, 거의 항상 global minimum에 도달합니다. BGD보다 noisy한 이유는, 어떤 샘플은 minimum으로 가는 좋은 샘플일 수도 있고 어떤 샘플은 minimum으로 가기 어려운 샘플일 수도 있기 때문입니다. 또한, SGD의 가장 큰 단점은 벡터화 과정에서 속도가 매우 느리다는 것입니다. 데이터 하나씩 처리하는 방식이기 때문에 매우 비효율적입니다.
- 장점 : local minimum에 빠질 위험이 적다.
- 단점 : Optimal을 찾지 못할 가능성이 있다.
다른 알고리즘에 비해 속도가 느리다. (뒤에서 Momentum,RMSprop,Adam과 비교하여 설명하겠습니다.)
MGD는 한 번의 iteration마다 n(1<n<m)개의 데이터를 사용하기 때문에 BGD와 SGD의 장점을 합친 알고리즘입니다. MGD를 사용하 때는 mini-batch size를 잘 설정해야 합니다.
mini-batch size 설정
- small training set (대략 m < 2000) -> BGD사용
- Typical mini-batch size :
1. 64, 128, 256, 512컴퓨터는 2진수로 계산되기 때문에 batch size는 대체로 2의n승으로 설정
2. 가 GPU/CPU에 모두 들어가게 설정(mini-batch쌍이 GPU/CPU 메모리에 들어가지 않는다면 성능은 더 악화됩니다.)
코드 구현
#python
weight[i] += - learning_rate * gradient
#tensorflow 2.x
tf.keras.optimizers.SGD(lr = 0.001)2. Momentum Algorithm (모멘텀)
Exponentially weighted averages(지수 가중 평균)
Momentum 알고리즘을 이해하기 위해서는 지수 가중 평균(Exponentially Weighted Average)(=지수 이동 평균)을 이해해야 합니다.
지수 가중 평균(=지수 이동 평균)이란, 데이터의 이동 평균을 구할 때, 오래된 데이터가 미치는 영향을 지수적으로 감쇠(exponential decay) 하도록 만들어 주는 방법입니다.
예를 들어, 런던의 일일 평균 날씨를 그래프로 나타내보았습니다.
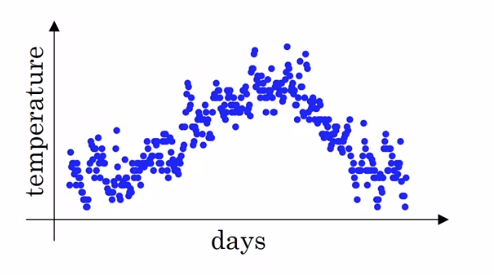
이 데이터는 nosiy하기 때문에 트랜드를 산출하기 위해서는 어떻게 해야 할까요?
(moving average)
단순히 전후 몇일간의 평균으로만 계산한다면(Moving Average) 오래된 데이터의 영향과 최신 데이터의 영향이 비슷해져 버리므로 우리가 원하는 추세를 나타낼 수 없을 것입니다.
이를 보완하기 위해 Weight를 부여하는 방식이 도입되었는데, 시간이 흐름에 따라 지수적으로 감쇠하도록 설계한 것이 지수 가중 평균입니다.
일단 으로 초기값을 설정합니다.
다음으로, 일 별로 모든 값을 평균화 합니다. value로 나오는 값을 0.9의 weight로 곱하고 0.1을 더한뒤, 그 날의 온도를 곱해줍니다.
v라는 날에 대한 공식의 일반화는 0.9(이전날짜v) + 0.1(그날의 온도)입니다.
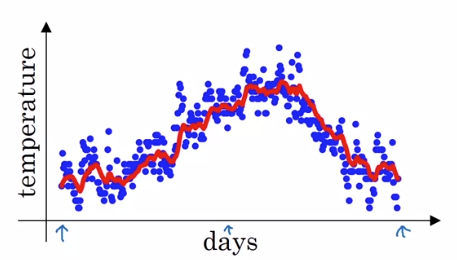
위 그래프의 빨간색 선이 지수 가중 평균 방식으로 구한 일별 날짜의 온도의 이동평균으로 나타낸 그래프입니다.
지수 가중 평균 식
( , :새로운 데이터, :현재의 경향)
위 지수 가중 평균의 식을 보면,
이고, 앞에 0~1사이의값이 곱해지므로, 오래된 데이터일수록 현재의 경향에 미치는 영향이 줄어든다는 것을 알 수 있습니다.
예전 데이터는 으로 지수적으로 빠르게 감소하게 되기 때문에, 지수적(Exponetially) 감쇠라고 부릅니다.
지수 가중 평균의 근사
지수 가중 평균의 근사 식
는 일의 데이터의 평균을 사용하여 근사합니다
예를들어
이면, 이전 10일의 온도의 평균이 그날의 이고(빨간색 그래프)
이면, 이전 50일의 온도의 평균이 그날의 이고(초록색그래프)
이면, 이전 2일의 온도의 평균이 그날의 입니다.(노란색 그래프)
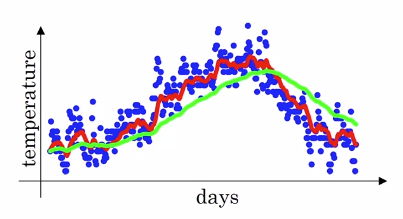
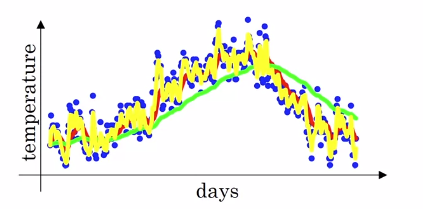
- 의 경우값이 1에 가까워, 많은 날을 고려하기 때문에 더 부드러운 그래프 모양이 나옵니다. 또한 더 큰 범위의 온도로 평균치를 구하기 때문에 그래프가 오른쪽으로 이동하였습니다.
이 경우, 이전 데이터에 의 큰 가중을 적용하고, 현재 데이터에 라는 작은 가중을 적용합니다. 최신 데이터보다는 과거의 데이터에 대한 비중이 큽낟. - 의 경우 훨씬 더 작은 범위의 평규치를 구하게 됩니다. 데이터가 더 noisy하고, 이상점에서 훨씬 취약하게 도비니다. 하지만, 기온변화를 빠르게 반영하게 됩니다.
에 따라 과거 데이터의 비중을 고려하는 이 공식을 지수 가중 평균 Exponentially weighted (moving) average라고 합니다.
바이어스 보정 (Bias Correction)
지수 가중 평균을 이용한 추정은 초기 구간에 오차가 있습니다.
머신러닝에서는 지수 가중 평균을 구현할 때 초기 구간을 기다린 후 사용하기 때문에 바이어스 보정을 신경쓰지 않습니다.
하지만, 초기 구간의 바이어스를 신경쓴다면 바이어스 보정을 사용해야 합니다. 바이어스 보정은, 기존에서 를 나누어 주면 됩니다.
Gradient descent with momentum
이제, 위에서 학습한 지수 가중 평균(Expoentially Weighted Average)을 적용해 보겠습니다. (이하 "가중 평균"이라고 표현된 것은 지수 가중 평균을 의미합니다.)
모멘텀 알고리즘이란, Gradient descent에서 기울기(gradient)의 가중 평균치를 산출하여 weight를 업데이트하는 것입니다. Momentum을 사용함으로써, 속도가 빠르고 SGD가 over shooting,diverging 되는 것을 방지하며 locla minimum 탈출이 가능합니다.
모멘텀(Momentum=Gradient descent with momentum)은 일반적인 Gradient Descent 알고리즘보다 빠르게 동작합니다.
앞서 말해듯, SGD(또는 MGD)는 다음과 같이 동작하게 됩니다.

위 그래프의 변동폭은 learning rate를 나타냅니다. 만약 learning rate를 작게한다면 학습속도가 너무 느리고, learning rate를 크게한다면 over shooting이나 diverging의 위험성이 있습니다. 따라서, opimal로 향하기 위해서는 가로축으로는 빠르게 전진해야하고, 세로축으로는 천천히 진행되어야 합니다.
weight의 derivative()에 대한 가중 평균치 velocity()를 구해 이 문제를 해결합니다.
기존 Gradient Descent Algorithm
Momentum Algorithm
()는 velocity를 라고 하고, 는 acceleration입니다.
총 두개의 하이퍼파라미터가 있습니다. 와 입니다.
는 learning reate이고, 는 momentum입니다. 지난 몇개의 기울기 강하의 평균치를 사용할 것인지에 대한 파라미터입니다. (지수 가중 평균의 . 머신러닝에서는 바이어스 보정은 거의 사용하지 않습니다.)
주로 로 사용합니다.(지난 10개의 기울기 강하의 평균치 사용)
대부분 을 1로 근사하여,
로 사용합니다.
위와 같은 momentum algorithm은 경사 하강(Gradient descent)를 smooth하게 만들어주어 over shooting, diverging을 막아줍니다.
코드
#python
v = beta * v - learning_rate * gradient
weight[i] += v
#tensorflow 2.x
tf.keras.optimizers.SGD(lr = 0.1, momentum = 0.9)3. RMSprop Algorithm
RMSprop은 Root Mean Square Propatation의 약자입니다. 이 알고리즘 역시 기울기 강하의 속도를 증가시키는 알고리즘 입니다.
기존 Gradient Descent Algorithm
RMSprop Algorithm
Momentum algorithm과 마찬가지로 지수 이동 평균이 적용되었습니다.

앞서 말해듯, SGD(또는 MGD)는 다음과 같이 동작하게 되고, 안정적으로 opimal로 향하기 위해서는 가로축으로 빠르게 전진해야하고 세로축으로는 천천히 진행되어야 합니다.
(위 그림에서 명료성을 위해 가로축을 ,세로축을 라고 하겠습니다.)
가로축을 빠르게 이동하고 싶다면 을 작게하여 를 크게할 수 있고,
세로축을 빠르게 이동하고 싶다면 을 크게하여 를 작게할 수 있습니다.
이는 하이퍼 파라미터인 로 조절할 수 있습니다.
코드
#python
beta2 = beta2 * s + (1 - beta2) * gradient**2
weight[i] += -learning_rate * gradient / (np.sqrt(s) + e)
#tensorflow 2.x
tf.keras.optimizers.RMSprop(learning_rate=0.001,rho=0.9) //rho가 beta_24. Adam Optimization Algorithm
아담(Adam)은 Adaptive Moment Estimation의 약자입니다. 모멘텀과 RMSprop을 섞어놓은 최적화 알고리즘 입기 때문에, 딥러닝에서 가장 흔히 사용되는 최적화 알고리즘 입니다.
Adam Optimization Algorithm
먼저 초기화를 진행하고, Momentum과 RMSprop에서 사용한 와 를 지정해줍니다..
또한, Momentum에서 소개한 Bias correction을 해주어야 합니다.
마지막으로 Momentum과 RMSprop의 가중치 업데이트 방식을 모두 사용하여 가중치 업데이트를 진행합니다.
Adam의 하이퍼 파라미터
: learning rate
: 1차 moment, 대부분 0.9 (의 지수 가중 평균 계산 )
: 2차 moment, 논문에서는 0.99 (과 의 지수 가중 평균 계산)
: 논문에서는 0.10^{-8} (성능에 거의 영향 X)
코드
# tensorflow2.x
tf.keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.99, epsilon=None)5. Opimization problem solving
Learning rate decay
Learning rate decay란, learning rate 를 천천히 줄여나가는 것입니다.
크기가 큰 를 유지한다면, 학습은 빠르지만 optima 부근에서 맴돌 뿐 정확히 수렴하기 어렵습니다.
크기가 작은 를 유지한다면, 학습이 매우 느릴 것입니다.
Learning rate decay를 사용하면 처음에는 learning rate 를 하여 빠르게 학습을 진행하고, 값이 점차 작아지면서 optima 부근의 매우 좁은 범위까지 집입할 수 있게 됩니다.
Learning rate decay method 1
Learning rate decay method 2 (exponential decay)
와 decay_rate모두 하이퍼 파라미터 입니다.
Local minimum
Loss function의 global minimum을 빠르고 정확하게 찾는 것이 최적화의 목적입니다.
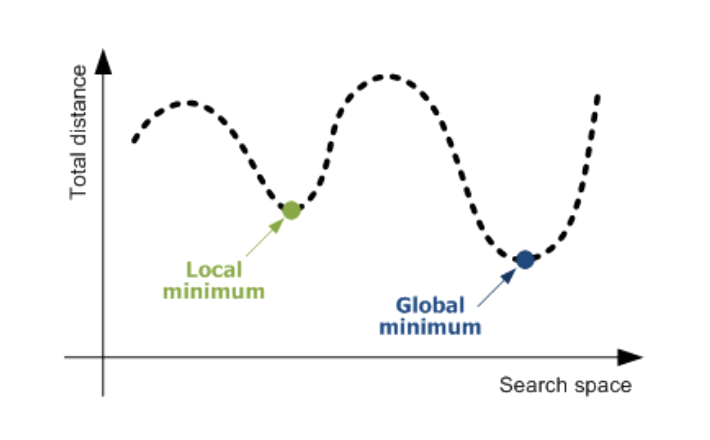
딥러닝 초기에는 최적화 알고리즘이 발달하지 않아 local minimum에 빠질 위험성이 있었습니다.
하지만 현재는 최적화 이론이 많이 발달하였고 고차원 공간에서 정의되는 Loss function에 대해 local minimum에 빠질 확률은 매우 작습니다. local minimum에 빠진다는 것은, 네트워크를 구성하는 모든 파라미터가 모두 local minimum에 빠져야하는데 아주 희박한 확률이기 때문입니다. 따라서 local minimum은 대부분 고려하지 않습니다.
Plateau
Plateau 현상이란, Loss function에 평지(Plateau)가 생겨 기울기가 0에 가까워져 loss가 업데이트 되지 않는 현상을 말합니다. 이 경우는 local minimum에 비해 일어날 확률이 높습니다.
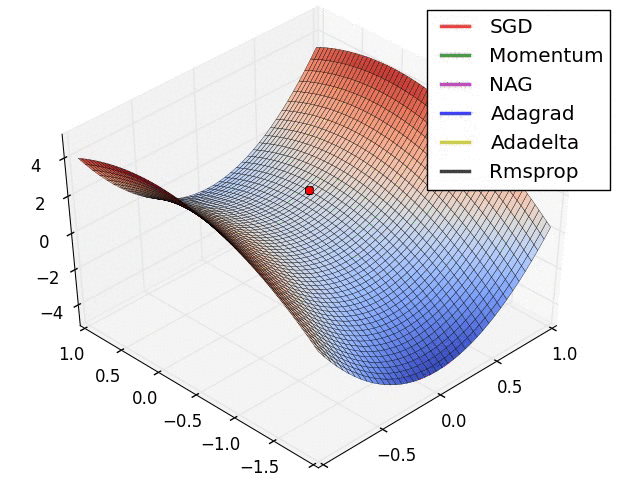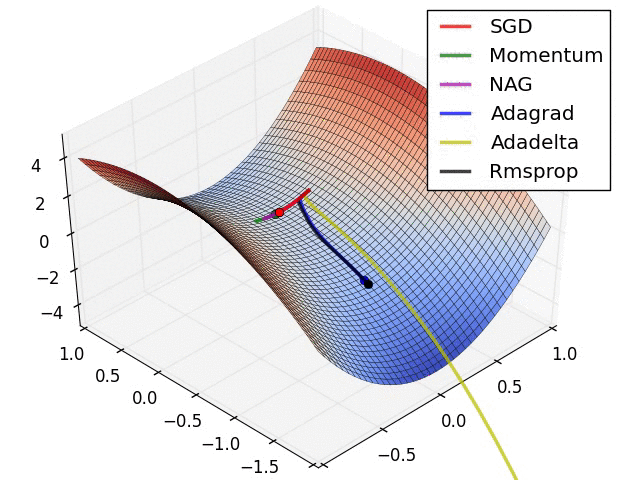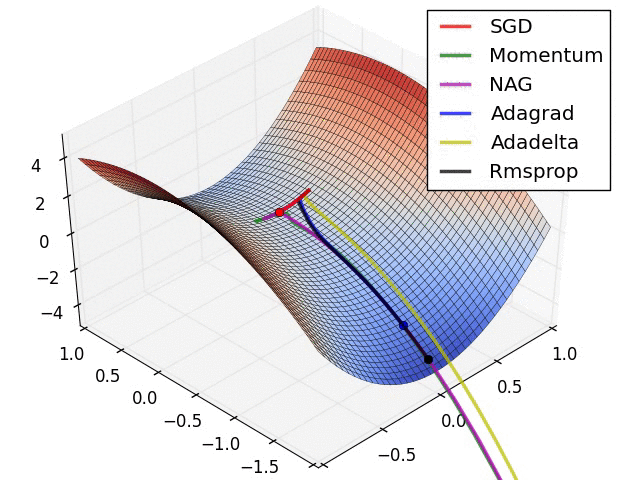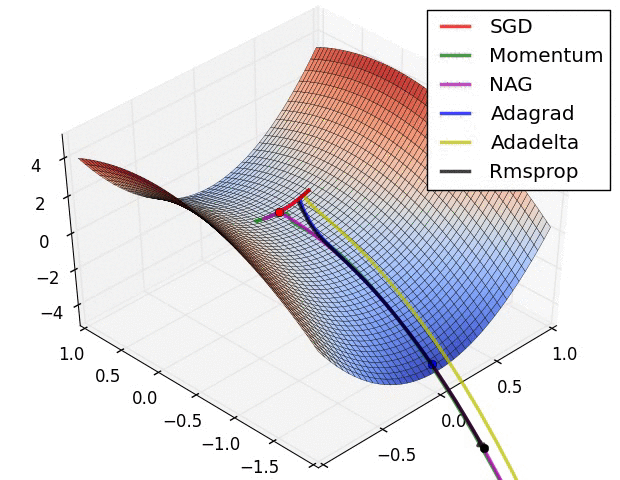
위 그래프에서 알 수 있듯 SGD는 Plateau에 취약합니다. 이 현상을 고려한다면, SGD가 아닌 RMSprp, Adam 등과 같은 Opimizer를 사용하는 것이 적절합니다.
reference :
https://www.coursera.org/learn/deep-neural-network/home
http://www.datamarket.kr/xe/index.php?mid=board_jPWY12&page=2&document_srl=66086
http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html
https://twinw.tistory.com/247
https://wjddyd66.github.io/dl/NeuralNetwork-(3)-Optimazation2/

