
💡깊이 우선 탐색
그래프 완전 탐색 기법 중 하나
그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘
완전 탐색
그래프에 있는 모든 노드를 탐색하는 것
특징
- 재귀 함수로 구현 ->
스택 오버플로에 유의해야 한다. - 스택 자료구조 이용
핵심 이론
한 번 방문한 노드를 다시 방문하면 안된다. -> 탐색한 곳을 다시 탐색한다는 것은 비효율적이기 때문이다.
따라서 노드 방문 여부를 체크할 배열이 필요하다. 그래프는 인접 리스트로 표현한다.
1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
자료구조: 인접 리스트
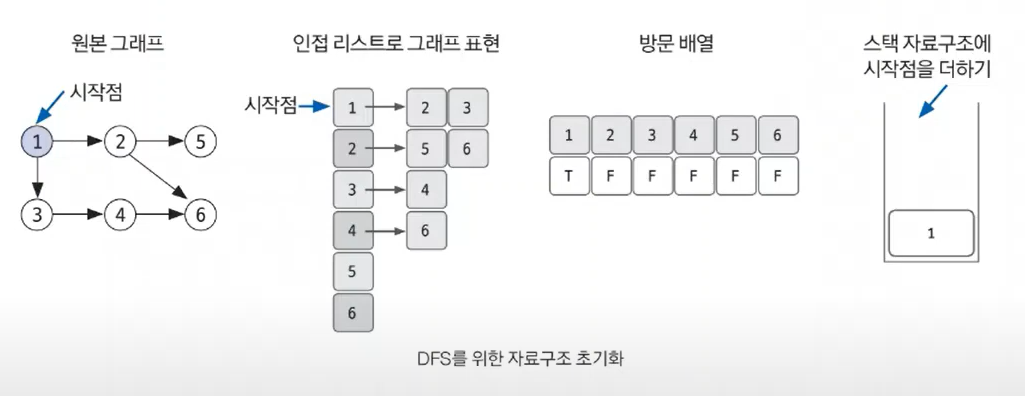
인접 리스트로 그래프 표현
1번에서 2번, 3번에 접근 가능
2번에서 5번, 6번에 접근 가능
3번에서 4번에 접근 가능
(이하 생략)
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
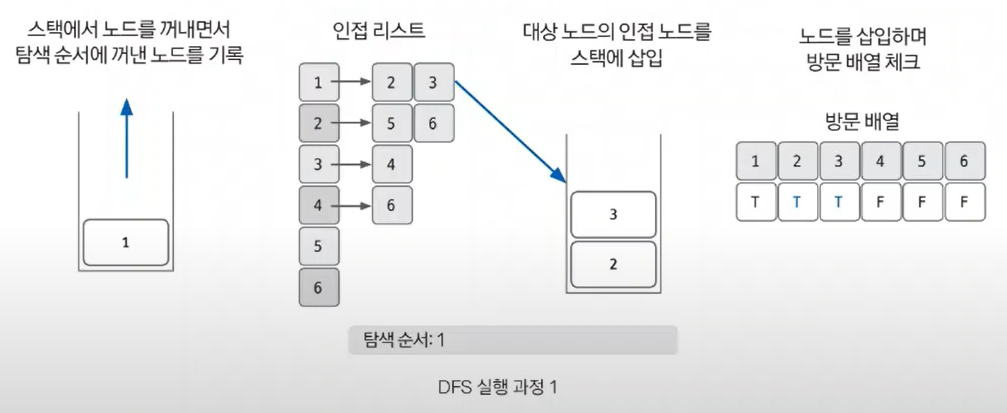
노드를 꺼내고, 꺼낸 노드의 인접 리스트를 확인한 후 인접 노드를 스택에 삽입한다.
이때 2와 3의 삽입 순서는 상관 없다. 2를 먼저 넣어도 되고 3을 먼저 넣어도 된다.
3. 스택 자료구조에 값이 없을 때까지 반복하기
위 과정을 스택 자료구조에 값이 없을 때까지 반복한다.
시작점을 기준으로 DFS를 돌렸을 떄 더이상 갈 수 있는 곳이 없다는 것을 의미한다. DFS가 끝났다는 것을 의미한다.
이때 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심이다.
인접 리스트를 확인한 후 인접 노드를 스택에 넣을 때 무조건적으로 넣는 것이 아니라 방문여부를 확인한 후 넣어야 한다. 이미 방문한 노드는 넣지 않고 스킵한다.
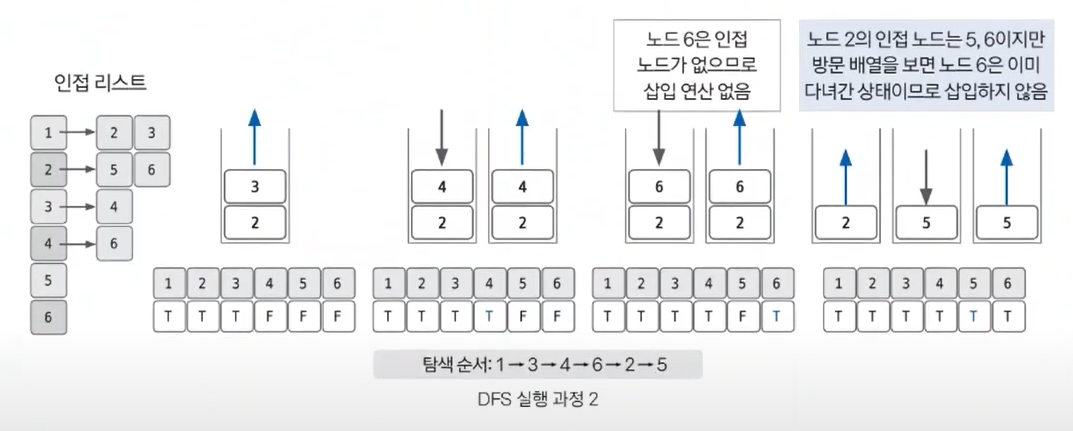
1의 인접노드 2, 3이 스택에 삽입
3이 꺼내지고 인접노드 4가 삽입
4가 꺼내지고 인접노드 6이 삽입
6이 꺼내지는데 인접노드가 없으므로 삽입 없음
2가 꺼내지고 인접노드 5가 삽입, 6은 이미 방문했기 때문에 스킵
5가 꺼내지고 DFS 종료
- 스택에 노드를 삽입할 때 방문 배열을 체크하고, 스택에서 노드를 뺄 때 탐색 순서에 기록하며 인접 노드를 방문 배열과 대조하여 살펴본다.
즉, 추가로 탐색할지 말지를 정할 때 이미 방문한 배열인지 아닌지를 방문배열을 기준으로 판단해서, 이미 방문한 노드이면 방문하지 않도록 스택에 넣지 않는다.
