분할 정복 알고리즘은 주어진 문제의 입력을 분할하여 문제를 해결하는 방식의 알고리즘이다.
분할한 입력에 대하여 동일한 알고리즘을 적용하여 해를 계산한다. 이 때, 분할된 입력에 대한 문제를 부분 문제(subproblem)이라고 하고, 부분 문제의 해를 부분 해라고 한다. 부분 문제를 더 이상 분할할 수 없을 때까지 분할한 다음, 이들의 부분 해를 취합하여 원래 문제의 해를 얻는다.

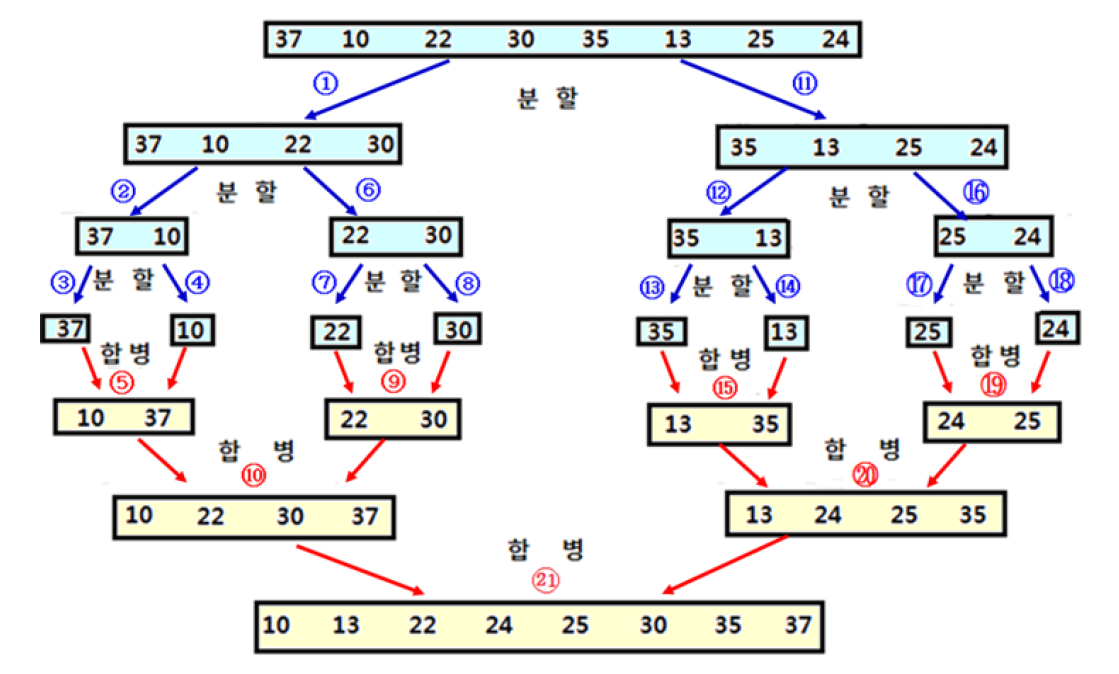
합병 정렬 (Merge Sort)

1. n개의 숫자들을 2개의 부분 문제로 $log_{2}n$번 분할
2. 2개의 정렬된 부분을 합병하여 정렬하는 과정 반복

(1) 분할하는 부분: 배열의 중간 인덱스 계산과 2회의 순환 호출이므로 $O(1)$ 시간이 소요
(2) 합병하여 정렬하는 부분: 각 층마다 모든 숫자가 합병에 참여하므로, 각 층마다 $O(n)$ 시간이 소요

따라서 합병 정렬의 시간 복잡도는 $log_{2}n * O(n) = O(nlogn)$이다.
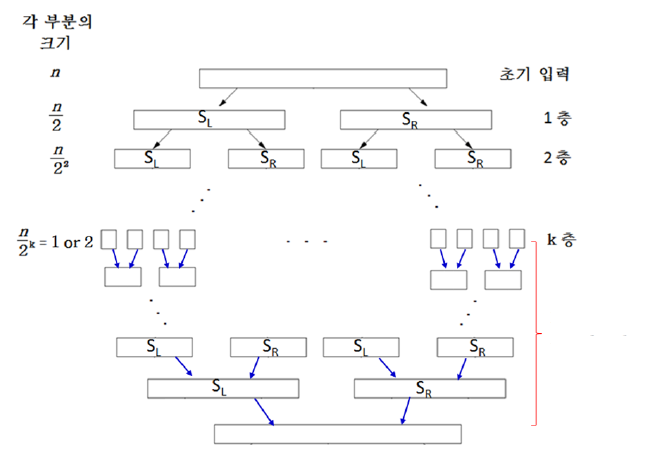
일반화하면, 시간 복잡도는 아래와 같이 구할 수 있다.

입력이 $a$개의 부분 문제로 분할되며 부분 문제의 크기가 $1/b$로 감소한다면,
각 문제마다 병합(정복)단계에서 걸리는 시간 $d$에 대해 $log_{b}a>d$에서
알고리즘의 시간 복잡도는 $O(n^{log_{b}a})$이다.

이 경우, a=2, b=2, d=n에서 $log_{2}2=1 < d=n$이므로 해당하지 않는다.

정렬해야하는 숫자가 많을수록 효율적인 정렬 알고리즘을 사용해야 제한 시간에 걸리지 않으므로, $O(n^2)$인 버블 정렬보다 $O(nlogn)$인 합병 정렬을 사용하는 것이 적합하다.

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define SIZE 15

void makeArray(int* list, int length);
void printArray(int* list, int length);
void merge(int* list, int* sorted, int left, int mid, int right);
void mergeSort(int* list, int* sorted, int left, int right);

int main() {
	int* list = malloc(sizeof(int) * SIZE); 			// 입력 배열
	int* sorted = malloc(sizeof(int) * SIZE);			// 합병 결과를 저장하는 임시 배열
	srand(time(NULL));
	makeArray(list, SIZE);
	printArray(list, SIZE);

	mergeSort(list, sorted, 0, SIZE - 1);
	printArray(list, SIZE);

	free(list);
	free(sorted);
}
void mergeSort(int* list, int* sorted, int left, int right) {
	int mid;
	if (left < right) { 									// left = right일때까지 분할
		mid = (left + right) / 2;
		mergeSort(list, sorted, left, mid);
		mergeSort(list, sorted, mid + 1, right);
		merge(list, sorted, left, mid, right);
	}
}
// 정렬된 두 리스트를 합병 및 정렬한다.
void merge(int* list, int* sorted, int left, int mid, int right) {
	int i = left, j = mid + 1, k=left;
	while (i <= mid && j <= right) {
		if (list[i] < list[j]) {
			sorted[k++] = list[i++];
		}
		else {
			sorted[k++] = list[j++];
		}
	}
	if (i > mid) { 										// 오른쪽 리스트에 원소가 남아있으면
		for (int l = j; l <= right; l++) {
			sorted[k++] = list[l];
		}
	}
	else { 												//  왼쪽 리스트에 원소가 남아있으면
		for (int l = i; l <= mid; l++) {
			sorted[k++] = list[l];
		}
	}
	// 합병 정렬한 결과를 list 배열에 저장 
	for (int l = left; l <= right; l++) {
		list[l] = sorted[l];
	}
}
void makeArray(int* list, int length) { 				// 배열 생성 함수
	for (int i = 0; i < length; i++) {
		list[i] = rand() % 100 + 1; 					// 1~100 난수 생성
	}
}
void printArray(int* list, int length) { 				// 배열 원소 출력 함수
	for (int i = 0; i < length; i++) {
		printf("%d\t", list[i]);
	}
	printf("\n");
}

SIZE=15에 대해 시행한 결과는 아래와 같다.

합병 정렬은 입력을 위한 메모리 공간 int list 이외에 int sorted가 추가로 필요하다. 즉, 2개의 정렬된 부분을 하나로 합병하기 위해 합병된 결과를 저장할 입력과 같은 크기의 공간 (임시 배열)이 필요하므로 메모리 공간을 많이 사용하는 단점이 있다.

퀵 정렬(QUick Sort)

문제를 크기가 일정하지 않은 2개의 부분 문제로 분할하는 분할 정복 알고리즘이다.
퀵 정렬은 피봇(pivot)을 기준으로 피봇보다 작은 숫자들은 왼편에, 피봇보다 큰 숫자들은 오른편에 위치하도록 분할하고 피봇을 그 사이에 놓는다. 이후, 분할된 부분 문제들에 대해서도 위와 동일한 과정을 수행하여 정렬한다.
피봇은 분할된 왼편이나 오른편 부분 문제에 속하지 않으며, 각 부분 문제의 크기가 1이 될 때까지 (left = right) 피봇을 제자리로 옮기고 분할하는 과정을 수행한다.

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define SIZE 15
#define SWAP(x,y,t) ((t)=(x),(x)=(y),(y)=(t))

void makeArray(int* list, int length);
void printArray(int* list, int length);
int partition(int* list, int left, int right);
void quickSort(int* list, int left, int right);
int main() {
	int* list = malloc(sizeof(int) * SIZE);
	srand(time(NULL));
	makeArray(list, SIZE);
	printArray(list, SIZE);

	quickSort(list, 0, SIZE - 1);
	printArray(list, SIZE);

	free(list);
}
void makeArray(int* list, int length) { 				// 배열 생성 함수
	for (int i = 0; i < length; i++) {
		list[i] = rand() % 100 + 1; 					// 1~100 난수 생성
	}
}
void printArray(int* list, int length) { 				// 배열 원소 출력 함수
	for (int i = 0; i < length; i++) {
		printf("%d\t", list[i]);
	}
	printf("\n");
}
// pivot을 기준으로 값을 이동시키고, pivot의 인덱스를 반환한다.
int partition(int* list, int left, int right) {
	int pivot = list[left]; 							// left 인덱스의 값을 피봇으로 선택
	int temp;
	int low = left;
	int high = right+1;
	do {
		do {
			low++;
		} while (list[low] < pivot); 					// list[low] >= pivot이면 break
		do{
			high--;
		} while (list[high] > pivot); 					// list[high] <= pivot이면 break
	
		if (low < high) {
			SWAP(list[low], list[high], temp); 			// pivot보다 크거나 같은 list[low]를 오른편으로, 작거나 같은 list[high]를 왼편으로 이동
		}
	} while (low < high);
	SWAP(list[left], list[high], temp); 				// pivot을 오른편과 왼편 사이 인덱스로 이동
	return high;
}
void quickSort(int* list, int left, int right) {
	if (left < right) { 								// left = right일때까지 partition 함수 실행 후 분할하는 과정 반복
		int p = partition(list, left, right);
		quickSort(list, left, p - 1);
		quickSort(list, p + 1, right);
	}
}

SIZE=15에 대해 시행한 결과는 아래와 같다.

퀵 정렬의 성능은 피봇 선택이 좌우한다. 피봇을 잘못 선택하면, 한 부분으로 치우치는 분할이 야기되기 때문이다. 피봇으로 매번 가장 작은 숫자, 또는 가장 큰 숫자가 선택되면 시간 복잡도는 O($n^2$)이 되고, 피봇으로 매번 중앙값이 선택되면 시간 복잡도는 (층수)*O(n) = O(nlogn)이 된다. 피봇을 항상 랜덤하게 선택한다고 가정하면, 평균의 경우 시간 복잡도는 O(nlogn)이다.

실제로 코테에서 정렬을 구현할 때는 std::sort함수를 사용하면 된다.

피봇을 랜덤하게 선정하는 방법에는 여러가지가 있다.

(1) Median-of-Three

가장 왼쪽 숫자, 중간 숫자, 가장 오른쪽 숫자중에서 중앙값을 피봇으로 선택한다.
(ex) 가장 왼쪽 숫자가 10, 중간 인덱스의 숫자가 5, 가장 오른쪽 숫자가 50이면 중앙값인 10을 피봇으로 선택.

int partition(int* list, int left, int right) {
	int temp;
	int low = left;
	int high = right+1;

	int mid = (left + right) / 2;
	int find_Med_index[3] = { left, mid, right };
	for (int i = 0; i < 2; i++) {
		for (int j = i + 1; j < 3; j++) {
			if (list[find_Med_index[i]] > list[find_Med_index[j]])
				SWAP(find_Med_index[i], find_Med_index[j], temp);
		}
	}
	int pivot = list[find_Med_index[1]]; // 가장 왼쪽 숫자, 중간 숫자, 가장 오른쪽 숫자의 중앙값을 피봇으로 선택
	SWAP(list[left], list[find_Med_index[1]], temp);

	do {
		do {
			low++;
		} while (list[low] < pivot); // list[low] >= pivot이면 break
		do{
			high--;
		} while (list[high] > pivot); // list[high] <= pivot이면 break
	
		if (low < high) {
			SWAP(list[low], list[high], temp); // pivot보다 크거나 같은 list[low]를 오른편으로, 작거나 같은 list[high]를 왼편으로 이동
		}
	} while (low < high);
	SWAP(list[left], list[high], temp); // pivot을 오른편과 왼편 사이 인덱스로 이동
	return high;
}

(2) Median-of-Medians

3등분 후, 각 부분에서 가장 왼쪽 숫자, 중간 숫자, 가장 오른쪽 숫자 중에서 중앙값을 찾고, 세 중앙값들 중에서 중앙값을 피봇으로 선택한다.

분할 정복 알고리즘 주의할 점

분할 정복 적용에 있어서 주의할 점은 (분할된 부분 문제의 입력 크기 합) > (분할 전 입력 크기)이 되지 않도록 해야한다는 점이다. 예를 들어, n번째의 피보나치 수를 구할 때 분할 정복 알고리즘을 적용하면 $F(n) = F(n-1) + F(n-2)$에서 (n-1) + (n-2) > n이 되어 분할 후 입력 크기가 거의 2배로 증가한다. 따라서 피보나치 수를 구하는 문제는 재귀 함수가 아닌 반복문을 사용하여 푸는 것이 바람직하다.
주의할 또 다른 점은 취합(정복) 과정이다. 입력을 분할만 한다고 해서 효율적인 알고리즘이 만들어지는 것은 아니므로, 취합 과정이 문제 해결에 잘 부합하는지 확인해야한다.

분할 정복 알고리즘을 사용하는 문제

(1) 최근접 점의 쌍 찾기

거리가 가장 가까운 한 쌍의 점을 찾아라.

n개의 점을 $1/2$로 분할하여 각각의 부분 문제에서 거리가 가장 가까운 점의 쌍을 찾고, 2개의 부분 해 중에서 짧은 거리를 가진 점의 쌍을 일단 찾는다. 이후, 중간 영역 안에 있는 점들 중에 더 근접한 점의 쌍이 있는지 확인한다.

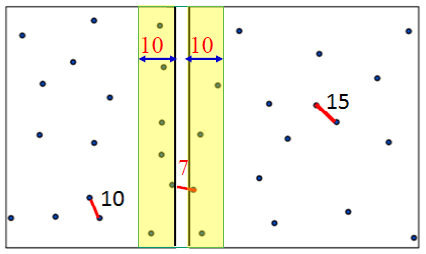
1. 배열에 x-좌표의 오름차순으로 점들을 정렬한다.
2. 왼쪽 부분의 최근접 점의 쌍 사이의 거리와 오른쪽 부분의 최근접 점의 쌍 사이의 거리 중 더 짧은 거리 값 $d$를 찾는다.
   즉, $d$ = $min$(왼쪽 부분의 최근접 점의 쌍 사이의 거리, 오른쪽 부분의 최근접 점의 쌍 사이의 거리)
3. 중간 영역에 속한 점을 찾는다.
   중간 영역은 x-좌표의 값이 (왼쪽 부분 문제의 가장 오른쪽 점의 x-좌표)-$d$에서 (오른쪽 부분 문제의 가장 왼쪽 점의 x-좌표)+$d$인 영역을 말한다.
4. 중간 영역에 속하는 점들 중 최근접 점의 쌍 사이의 거리를 찾고, d와 비교하여 더 짧은 거리를 반환한다.

이를 의사 코드(pseudo code)로 정리하면 아래와 같다.

ClosestPair(S)
입력: x-좌표의 오름차순으로 정렬된 배열 S에 있는 i개의 점. (단, 각 점은 (x, y)로 표현
출력: S에 있는 점들 중 최근접 점의 쌍의 거리
1. if (i==2) return (2개의 점 사이의 거리)
2. else if (i==3) return (3개의 점들 사이의 최근접 점의 쌍 사이의 거리)
else{
3. 정렬된 S를 같은 크기의 $S_L$, $S_R$로 분할 (|S|가 홀수면 |$S_L$|=|$S_R$|+1이 되도록 분할)
4. $CP_L$ = ClosestPair($S_L$)
5. $CP_R$ = ClosestPair($S_R$)
6. $d$ = min($CP_L$, $CP_R$)
7. 중간 영역에 속하는 점들 중 최근접 점의 쌍 사이의 거리인 $CP_C$ 계산
8. return min($d$, $CP_C$)
}

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define SIZE 15
#define SWAP(a,b,t) ((t)=(a),(a)=(b),(b)=(t))
#define MIN(a,b) ((a)>=(b)?(b):(a))

typedef struct _Point{
  int x;
  int y;
} Point;

void makeArray(Point* arr,int size);
void printArray(Point* arr,int size);
void insertSort(Point* arr, int size, char opt);
double ClosestPair(Point* arr, int left, int right);

int main()
{
    Point* List = malloc(sizeof(Point)*SIZE);
    srand(time(NULL));
    makeArray(List, SIZE);
    
    insertSort(List, SIZE, 'x'); // x좌표 오름차순으로 점들을 정렬
    printArray(List, SIZE); 
    printf("%.2f",ClosestPair(List, 0, SIZE-1)); // 최근접 점의 쌍 사이의 거리 출력
    
    free(List);
    return 0;
}
void makeArray(Point* arr, int size){
    for(int i=0; i<size; i++){
        arr[i].x = rand()%100+1;
        arr[i].y = rand()%100+1;
    }
}
void printArray(Point* arr, int size){
    for(int i=0; i<size; i++){
        printf("(%d, %d)\t",arr[i].x,arr[i].y);
    }
    printf("\n");
}
void insertSort(Point* arr, int size, char opt){ // opt에 x or y 입력. x 혹은 y좌표 오름차순으로 삽입정렬 수행
    int min;
    Point temp;
    for(int i=0; i<size-1; i++){
        min = i;
        for(int j=i+1; j<size; j++){
            if(opt=='x'){
                if(arr[min].x>arr[j].x){
                    min = j;
                }
            }
            else{
                if(arr[min].y>arr[j].y){
                    min = j;
                }
            }
        }
        SWAP(arr[min],arr[i],temp);
    }
}
double dist(Point A, Point B){ // 두 점 사이의 거리 계산 함수
    return sqrt(pow(abs(A.x-B.x),2)+pow(abs(A.y-B.y),2));
}
double ClosestPair_center(Point*arr, int left, int mid, int right, double d){ // 중간영역의 최근접 점의 쌍 사이의 거리 계산 함수
    int min_x = arr[mid].x-d;
    int max_x = arr[mid].x+d;
    int start = right; // 중간 영역 점들 중 x좌표가 최소인 점의 인덱스
    int size = 0; // 중간 영역에 속한 점의 개수
    for(int i=left; i<=right; i++){
    	if(arr[i].x>=min_x && arr[i].x<=max_x){ // 중간 영역에 속한 점이면
        	if(start>i) start = i;
            size++;
        }
    }
    Point* arr_temp = malloc(sizeof(Point)*size);
    for(int i=0; i<size; i++){
    	arr_temp[i] = arr[start+i];
    }
    insertSort(arr_temp, size, 'y'); // 중간 영역에 속한 점들을 y-좌표 오름차순으로 정렬
    double CPC = -1;
    if(size>1){ // 중간 영역에 점이 2개 이상일 때
    	for(int i=0; i<size-1; i++){
        	for(int j=i+1; j<size; j++){
            	if(dist(arr[i],arr[j])<d){ // arr[i]와 거리가 d 이내인 점일 때
                	if(CPC==-1) CPC = dist(arr[i],arr[j]);
                	else CPC = MIN(CPC, dist(arr[i],arr[j]));
                }
            }
        }
    }
    free(arr_temp);
    return CPC;
}
double ClosestPair(Point* arr, int left, int right){ // 최근접 점의 쌍 사이의 거리 계산 함수
    int size = right-left+1;
    if(size==2) return dist(arr[left],arr[right]);
    else if(size==3){
        double d1 = dist(arr[left+2],arr[left+1]);
        double d2 = dist(arr[left+1],arr[left]);
        double d3 = dist(arr[left+2],arr[left]);
        return MIN(MIN(d1,d2),d3);
    }
    else{
        int mid = (left+right)/2;
        double CPL = ClosestPair(arr,left,mid);
        double CPR = ClosestPair(arr,mid+1,right);
        double d = MIN(CPL, CPR);
        
        double CPC = ClosestPair_center(arr, left, mid, right, d);
        return CPC!=-1 ? MIN(d,CPC) : d;
    }
}

S의 점을 x-좌표로 정렬하는데 $O(nlogn)$, S에 3개 이하의 점이 있는 경우 거리 계산에 $O(1)$, $S_L$과 $S_R$으로 분할하는데 배열이 정렬된 상태에서 중간 인덱스로 분할하면 되므로 $O(1)$, $S_L$과 $S_R$에 대하여 ClosePair를 호출하는 과정은 분할하며 호출하는 합병 정렬과 동일하게 $O(nlogn)$이 걸린다.
이후 중간 영역의 최근접 점의 쌍 사이의 거리를 구하는 과정은 중간 영역의 점들을 y-좌표로 정렬하는데 $O(nlogn)$, 각 점에서 주변의 점 사이의 거리를 계산하는데 $O(1)$, $CP_L$, $CP_R$, $CP_C$중 가장 짧은 거리를 구하는데 $O(1)$으로 총 $O(nlogn)$ 시간이 걸리며, 이 과정은 k층까지 분할된 후 층별로 수행되므로 $(층의 수) * O(nlogn) = logn * O(nlogn) = O(nlog^{2}n)$시간이 걸린다.

(2) 2개의 n-bit 정수의 곱

(2-1) O($n^2$)의 알고리즘으로 풀어보자.

2개의 n-bit 정수를 a, b라고 하자. a와 b를 각각 반으로 분할하고 분할한 부분을 $a_H, a_L, b_H, b_L$이라고 하면 a와 b는 아래와 같이 표현할 수 있다.

$a = 2^{n/2}*a_H +a_L$ , $b = 2^{n/2}*b_H +b_L$
(ex) 1011 = $2^2 *(10)+11$

따라서 a와 b의 곱은 아래와 같이 4개의 $n/2bit*n/2bit$ 곱셈으로 분할할 수 있다.

$a*b=2^n * a_{H}b_{H}+2^{n/2}*(a_{H}b_{L}+a_{L}b_{H})+a_{L}b_{L}$

이를 분할 정복 알고리즘에 이용하면 $a_H, a_L, b_H, b_L$의 길이가 1bit이 될 때까지 분할한 다음, 취합(정복)하는 과정을 통해 a와 b의 곱을 구할 수 있다.

시간 복잡도는 부분 문제가 4개씩 분할되고, 부분 문제의 크기가 $1/2$씩 줄어들고, 각 문제마다 병합(정복) 단계에서 걸리는 시간이 1이므로, $log_{2}4>1$에서 $O(n^{log_{2}4})=O(n^2)$이다. 좀 더 자세히 정리해보면, 2개의 $k$비트짜리 이진수를 더하는 알고리즘의 시간 복잡도는 $O(k)$이므로

$T(n) = 4T(n/2) + O(n)$

   $= ...$

   $= 4^{log_{2}n}T(1)+[O(n)+4O(n/2)+...+4^{log_{2}n}O(n/2^{log_{2}n})]$

   $= n^{log_{2}4}T(1)+[O(n)+4O(n/2)+...+n^{log_{2}4}O(n/n^{log_{2}2})]$

   $= n^{2}T(1)+[O(n)+4O(n/2)+...+n^{2}O(1)]$

따라서 시간 복잡도는 $O(n^2)$이다.

(2-2) O($n^{log_{2}3}$)의 알고리즘으로 풀어보자.

a와 b의 곱은 아래와 같이 $a_{H}b_{H}, a_{L}b_{L}, (a_H +a_L)(b_H +b_L)$으로 분할하여 계산할 수 있다.

$a*b=2^n * a_{H}b_{H}+2^{n/2}*(a_{H}b_{L}+a_{L}b_{H})+a_{L}b_{L}$

   $=2^n * a_{H}b_{H}+2^{n/2}*((a_H +a_L)(b_H +b_L)-a_{H}b_{H}-a_{L}b_{L})+a_{L}b_{L}$

시간 복잡도는 부분 문제가 3개씩 분할되고, 부분 문제의 크기가 $1/2$씩 줄어들고, 각 문제마다 병합(정복) 단계에서 걸리는 시간이 1이므로, $log_{2}3>1$에서 $O(n^{log_{2}3})$이다. 좀 더 자세히 정리해보면, 2개의 $k$비트짜리 이진수를 더하는 알고리즘의 시간 복잡도는 $O(k)$이므로

$T(n) = 3T(n/2) + O(n)$

   $= ...$

   $= 3^{log_{2}n}T(1)+[O(n)+3O(n/2)+...+3^{log_{2}n}O(n/2^{log_{2}n})]$

   $= n^{log_{2}3}T(1)+[O(n)+4O(n/2)+...+n^{log_{2}3}O(1)]$

따라서 시간 복잡도는 $O(n^{log_{2}3})$이다.
의사 코드(pseudo code)로 정리하면 다음과 같다.

$product(a, b, n)$
입력: 이진수 a, b, 그리고 a와 b의 비트수 n
출력: $a*b$
1. if(n==1) return $a*b$
2. a를 $a_H ,a_L$ 로 분할
3. b를 $b_H ,b_L$ 로 분할
4. $m1 = product(a_H, b_H, n/2)$
5. $m2 = product(a_L, b_L, n/2)$
6. $m3 = product(a_H +a_L, b_H +b_L, n/2)$
7. return $2^{n}$*$m1+2^{n/2}(m3-m1-m2)+m2$

(3) 2개의 n x n 행렬 곱

O($n^{2.81}$) 알고리즘으로 풀어보자.

2 x 2 행렬 곱을 생각해보자.
$a_{11}$   $a_{12}$ x $b_{11}$   $b_{12}$  = $a_{11}b_{11}+a_{12}b_{21}$  $a_{11}b_{12}+a_{12}b_{22}$
$a_{21}$   $a_{22}$   $b_{21}$   $b_{22}$    $a_{21}b_{11}+a_{22}b_{21}$  $a_{21}b_{12}+a_{22}b_{22}$

일반적으로, 2 x 2 행렬의 곱을 구하기 위해선 곱하기 연산이 8번, 더하기 연산이 4번 수행된다.
하지만 아래와 같이 계산하면 곱하기 연산이 7번, 더하기/빼기 연산이 18번 수행된다.

m1 = $(a_{11}+a_{22})(b_{11}+b_{22})$
m2 = $(a_{21}+a_{22})b_{11}$
m3 = $a_{11}(b_{12}-b_{22})$
m4 = $a_{22}(b_{21}-b_{11})$
m5 = $(a_{11}+a_{12})b_{22}$
m6 = $(a_{21}-a_{11})(b_{11}+b_{12})$
m7 = $(a_{12}-a_{22})(b_{21}+b_{22})$

아래는 m1~m7으로 표현된 행렬 곱이다.

$m1+m4-m5+m7$     $m3+m5$

   $m2+m4$     $m1+m3-m2+m$6

이 방법은 슈트라센(Strassen) 방식으로, n x n 행렬을 2 x 2 행렬처럼 $n/2$ x $n/2$ 행렬로 분할하여 계산한다. n이 클수록 일반적인 행렬 곱 방식보다 더 효율적이게 행렬 곱을 계산한다.

시간 복잡도는 부분 문제가 7개씩 분할되고, 부분 문제의 크기가 $1/2$씩 줄어들고, 각 문제마다 병합(정복) 단계에서 걸리는 시간이 2이므로,

$T(n) = 7T(n/2)+18(n/2$ x $n/2)$

따라서 시간 복잡도는 $log_{2}7>2$에서 $O(n^{log_{2}7})=O(n^{2.81})$이다.