행렬은 선형변환
행렬은 크기와 방향(고윳값 , 고유벡터)로 나눌 수 있음.
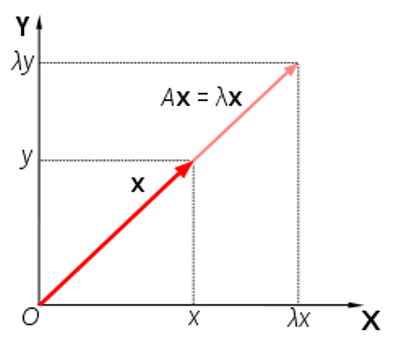
고윳값,고유벡터
- (Eigen Value, Eigen Vector)
- 선형변환(A)를 할 때 크기만 변하고 방향이 변하지 않는 벡터
e, v = np.linalg.eig(A)
v = v.T # 열 순서로 반환하므로 Transpose한다.
Thus, Eigen_value e[i]의 Eigen_vector는 v[i]- Eigen value & vector 특징
- 방향x , 크기만 갖는다.
- 고유벡터 방향으로 얼마나 큰지를 의미
- 고윳값이 큰 순서대로 고유벡터를 정렬하면 PCA의 주성분을 구할 수 있음
- 정보량이 많으므로
- 고윳값이 복소수라면 회전의 의미
- 고윳값 개수 = Rank
- 방향x , 크기만 갖는다.
Eigen Decomposition(고윳값 분해)

2번의 det(행렬식)을 사용하는 이유는 고유벡터 x가 영벡터가 되면 안되기 때문
If det(A) = 0: 역행렬을 갖지 않음 -> 역행렬이 존재하면 x벡터가 영벡터가 됨
단, 고윳값 분해는 정사각 행렬에서만 사용가능.
직사각행렬은 특이값분해(SVD)
공분산
- Corvariance
- 공분산행렬은 각 feature의 변동이 얼마나 닮았는지 나타냄
공분산은 feature가 2개 존재하면 2*2행렬로 나타낼 수 있음
x는 (n,2)의 데이터
x.T @ x = (2,n) @ (n,2) = (2,2)
PCA
- 고유값이 가장 큰 순서로 고유벡터를 주성분으로 할 수 있고 , 고유벡터에 정사영한 data의 variance(분산)이 가장 커지게 된다.
라그랑주 승수법에 나온 결과를 통해 Eigen_vector에 정사영을 하면 variance는 Eigen_value가 된다.
How many dimension?
- d차원을 m차원으로 감소시킨다고 가정하면 d*d차원의 Eigen value를 계산할 수 있음. (이때 데이터의 공분산행렬이 full rank임을 가정)
-
전체 data의 90%의 variance를 포함하는 m차원을 선택
- 이때 variance = Eigen value
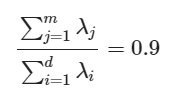
-
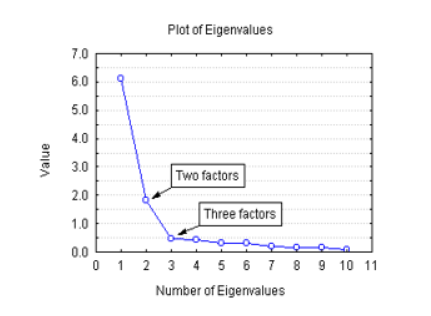
그래프를 통해 적절한 elbow선택
- elbow는 그래프가 확 꺾이는 지점
- x축은 Eigen value크기 순으로 정렬 후 선택한 m개의 차원 , y축은 해당 차원의 variance의 합
즉, PCA는 공분산행렬에 대해서 SVD를 한것이라 할 수 있음!!!!!!!!!!
LDA
- pca는 분산을 크게 하는 것이 목표라면
- LDA는 같은 class의 분산은 작게, 다른 class의 분산은 크게 하는 것이 목표
SVD
A 행렬이 (3,2)라하면 A.T@A 와 A@A.T의 고윳값을 구하면 된다
각각 (3,3) (2,2)행렬이지만 고윳값은 동일하게 나옴
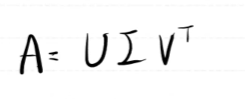
m->n변환이라면
A는 (n,m)
U는 (n,n) 시그마는 (n,m) VT는(m,m)
U와 V는 orthogonal matrix로 U@UT=I
U는 n차원의 축(서로 직교) V는 m차원의 축 VT로 나오므로 Transepose해야함
시그마는 diagnol matrix로 대각 원소는 eigen value 행이나 열에 0으로 채워서 차원 맞춰야함

t-SNE 와 PCA차이
-
pca는 고윳값 분해를 통해 중요한 고유벡터만 나머지 벡터는 제외 , 중요한 고유벡터에 매핑하는 *Feature Extraction한 방법이며 선형 변환이다.(고유벡터에 단순 행렬곱하므로)
-
또한 pca는 새로운 feature를 생성하는 것이며 기존의 feature들과는 독립적이다.
-
반면 t-Distributed Stochastic Neighbor Embedding(t-SNE)는 비선형적인 차원 축소 방법이며 고차원의 데이터 시각화에 성능이 좋다.
- 직관적으로 표현하면 고차원의 데이터를 저차원 데이터로 바꾸고 확률밀도에 비례하여 고차원 데이터의 분포와 저차원 데이터의 분포를 최소화하는 방식으로 학습함. (변환 전-후의 KL divergence를 최소화)
- 반면 t-SNE의 주 목적은 시각화 (기존의 feature 특성은 사라지므로, 단순히 클러스터링의 목적임)
<코드>
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
# MNIST 데이터 불러오기
data = load_digits()
# 2차원으로 차원 축소
n_components = 2
# t-sne 모델 생성
model = TSNE(n_components=n_components)
# 학습한 결과 2차원 공간 값 출력
print(model.fit_transform(data.data))
- n_components
데이터 타입 : int
기본값 : 2
의미 : 차원 축소 결과 임베딩되는 차원- perplexity
데이터 타입 : float
기본값 : 30.0
의미 : 다른 manifold learning의 nearest neighbors 갯수에 사용되는 값을 뜻합니다. 일반적으로 더 큰 데이터 셋은 보통 더 큰 perplexity 값을 필요로 합니다. 이 값을 정할 때, 5 ~ 50 사이의 값을 선택해 보고 더 좋은 결과를 얻기 위해서 값을 변경해 가면서 조정할 필요가 있습니다.- early_exaggerattion
데이터 타입 : float
기본값 : 12.0
의미 : 기존 공간에서 데이터의 클러스터 간 거리가 타겟 공간에서 얼만큼 조밀하거나 먼 지 나타내는 파라미터 입니다. 이 값을 큰 값으로 설정할 경우 기존 공간의 클러스터 사이의 공간이 타겟 공간에서 더 커지도록 학습됩니다. 이 매개 변수의 선택은 크게 중요하지는 않으나 학습 초기에 비용 함수가 증가하면 early_exaggeration 또는 initial learning rate가 너무 높을 수 있으니 이 경우 살펴 보면 됩니다.- learning_rate
데이터 타입 : float
기본값 : 200.0
의미 : 학습을 할 때 사용하는 learning rate 이며 일반적으로 10 ~ 1000 사이의 값을 가집니다. learning rate가 너무 높으면 데이터가 가장 가까운 이웃과 거의 같은 거리에있는 ‘공’처럼 보일 수 있습니다. 반면 learning rate가 너무 낮으면 대부분의 포인트가 특이치가 거의 없는 조밀 한 클라우드에서 압축 된 것처럼 보일 수 있습니다.- n_iter
데이터 타입 : int
기본값 : 1000
의미 : 최적화를 위한 최대 반복 횟수입니다. 이 값은 최소 250 이상이어야 학습하는 데 지장이 없습니다.- n_iter_without_progress
데이터 타입 : int
기본값 : 300
의미 : 성능 개선 없이 학습이 지속되면 학습을 중지하는 옵션이며 카운트는 50의 배수 단위로 카운트 됩니다.
