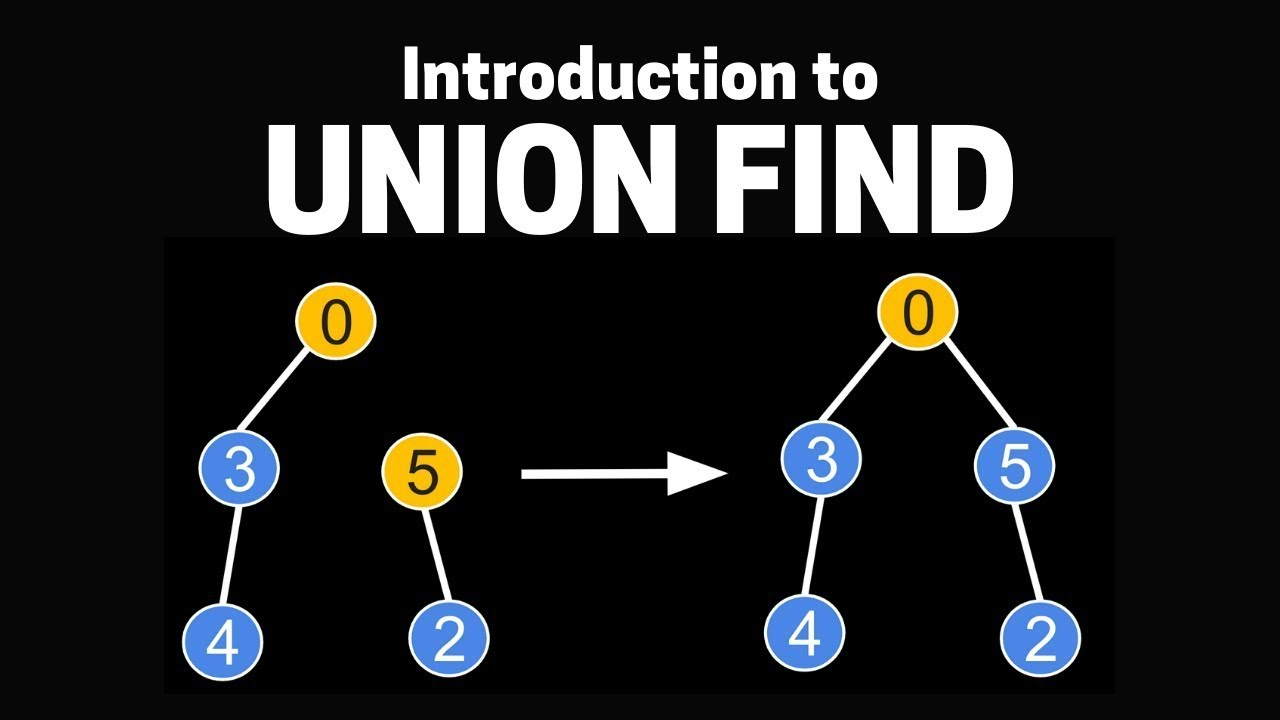
Union-Find
유니온-파인드 알고리즘은 그래프의 연결 여부를 확인하는 알고리즘으로, 노드를 연결하는 간선들의 정보가 주어졌을 때 특정 노드 두 개가 서로 연결되어 있는지, 즉 같은 그래프에 속하는지를 판별하기 위한 알고리즘이다. 이때 '서로소 집합'의 개념을 이용하여, 각 그래프들이 공통으로 가지고 있는 요소(부모 노드)를 비교함으로써 두 그래프의 연결 여부를 확인할 수 있다.
노드를 합치는 Union 연산과 노드의 루트 노드가 무엇인지를 찾아내는 Find 연산으로 이루어져 이런 이름이 붙었다.
대략적인 동작 과정을 정리하면 다음과 같다.
1. 간선 정보([n, m])를 확인하여 서로 연결된 두 노드(n, m)을 확인한다.
2. 두 노드 n, m의 각각의 루트 노드인 n', m'을 찾아낸다. - Find 연산
3. n'과 m' 중 값이 작은 노드를 부모 노드로 가정하여 연결시킨다. - Union 연산
4. 간선 정보들을 모두 순회하며 1~3 과정을 반복한다.
Example
1번부터 6번까지의 노드들과 그 간선의 정보 [[1, 4], [2, 3], [2, 4], [5, 6]]이 주어졌다고 하자. 각 노드들이 연결되어 있는지를 확인하기 위한 과정은 다음과 같이 정리할 수 있다.
-
부모 노드 초기화
각 노드의 수만큼 부모 노드 테이블을 만들고, 각 노드별로 자기 자신을 값으로 하도록 초기화한다.노드 1 2 3 4 5 6 부모 노드 1 2 3 4 5 6 -
간선 정보를 통해 루트 노드를 찾아 연결한다.
2-1. [1, 4]
1과 4가 연결되었으므로 두 노드의 부모 노드 값을 비교하여 더 작은 값(1)을 부모 노드로 설정한다.노드 1 2 3 4 5 6 부모 노드 1 2 3 1 5 6 2-2. [2, 3]
마찬가지로 둘 중 더 작은 값을 부모 노드로 설정한다.노드 1 2 3 4 5 6 부모 노드 1 2 2 1 5 6 2-3. [2, 4]
2와 4의 부모 노드 값을 각각 비교하면 4의 부모 노드 값이 1로 2의 부모 노드 값보다 더 작으므로 2의 부모 노드 값을 1로 설정한다.노드 1 2 3 4 5 6 부모 노드 1 1 2 1 5 6 2-4. [5, 6]
노드 1 2 3 4 5 6 부모 노드 1 1 2 1 5 5 → 연산 완료 후의 부모 노드 값
이때 3번 노드의 경우 부모 노드가 2로 되어 있으나, 2번 노드의 부모 노드 값이 1이므로 결과적으로 3번 노드 역시 루트 노드는 1이 된다. 이와 같이 3 → 2 → 1로 이어지는 재귀 과정을 줄이기 위해 부모 노드의 값을 미리 정해 버리는
압축 경로라는 테크닉을 사용할 수 있다.
코드 구현
이제 이 과정을 코드로 구현해 보자.
Find 연산
Find 연산은 부모 노드의 집합과 해당 노드의 번호를 값으로 받는다.
def find(parent, x):
# 자기 자신이 루트 노드가 아닐 경우 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
# return find(parent, parent[x])
parent[x] = find(parent, parent[x]) # 불필요한 재귀를 줄이기 위해 테이블 즉시 갱신
return parent[x]Union 연산
Union 연산은 위의 Find 연산을 이용해 각각의 노드를 연결한다. 즉, '간선'의 역할을 한다. 다만, 이때 간선 정보와는 달리 '루트 노드'의 값을 리턴함으로써 해당 노드들을 연결한다는 점이 차이가 있다.
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
# 각각의 부모 노드 값을 비교하여 작은 값으로 갱신
if a < b:
parent[b] = a
else:
parent[a] = b종합
이제 위에서 들었던 예시를 실제 전체 코드로 구현해 보자. 노드의 총 개수와 간선의 정보가 입력으로 주어진다.
# 1번 노드부터 6번 노드까지 존재하는 그래프로 가정
edges = [[1, 4], [2, 3], [2, 4], [5, 6]] # 간선 정보
n = len(edges) # 노드의 개수
# 부모 노드 테이블 생성 후 초기화
parent = [0] * (n+1)
for i in range(1, n+1):
parent[i] = i
# find 함수와 union 함수 선언
def find(parent, x):
# 자기 자신이 루트 노드가 아닐 경우 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
# return find(parent, parent[x])
parent[x] = find(parent, parent[x]) # 불필요한 재귀를 줄이기 위해 테이블 즉시 갱신
return parent[x]
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
# 각각의 부모 노드 값을 비교하여 작은 값으로 갱신
if a < b:
parent[b] = a
else:
parent[a] = b
# 부모 노드 값 갱신
for edge in edges:
a, b = edge
union(parent, a, b)
# 각 원소가 속한 집합 출력
print("각 원소가 속한 집합:", end=" ")
for i in range(1, n+1):
print(find(parent, i), end=" ")
print()
# 부모 테이블 내용 출력
print("부모 테이블:", end=" ")
for i in range(1, n+1):
print(parent[i], end=" ")> 각 원소가 속한 집합: 1 1 1 1 5 5
> 부모 테이블: 1 1 1 1 5 5 Union-Find를 이용한 사이클 판별
Union-Find 연산을 이용해 무방향 그래프에 대하여 사이클을 판별할 수 있다.
- 각 간선을 확안하면서 두 노드의 루트 노드를 확인한다.
1-1. 루트 노드가 서로 다를 경우 union 연산을 수행한다.
1-2. 루트 노드가 서로 같다면 사이클이 발생하는 것으로 간주한다. - 모든 간선에 대하여 상기 과정을 반복한다.
def check_cycle(edges):
cycle = False
for edge in edges:
a, b = edge
if find(parent, a) == find(parent, b):
cycle = True
break
else:
union(parent, a, b)
if cycle:
print("사이클이 존재합니다.")
else:
print("사이클이 존재하지 않습니다.")edges = [[1, 4], [2, 3], [2, 4], [5, 6]]
n = len(edges)
parent = [0] * (n+1)
for i in range(1, n+1):
parent[i] = i
check_cycle(edges)> 사이클이 존재하지 않습니다.edges = [[1, 4], [2, 3], [2, 4], [1, 3]]
n = len(edges)
parent = [0] * (n+1)
for i in range(1, n+1):
parent[i] = i
check_cycle(edges)> 사이클이 존재합니다.