[Programmers/Python] 시소 짝궁

Programmers - 시소 짝궁

문제

어느 공원 놀이터에는 시소가 하나 설치되어 있습니다. 이 시소는 중심으로부터 2(m), 3(m), 4(m) 거리의 지점에 좌석이 하나씩 있습니다.
이 시소를 두 명이 마주 보고 탄다고 할 때, 시소가 평형인 상태에서 각각에 의해 시소에 걸리는 토크의 크기가 서로 상쇄되어 완전한 균형을 이룰 수 있다면 그 두 사람을 시소 짝꿍이라고 합니다. 즉, 탑승한 사람의 무게와 시소 축과 좌석 간의 거리의 곱이 양쪽 다 같다면 시소 짝꿍이라고 할 수 있습니다.
사람들의 몸무게 목록 weights이 주어질 때, 시소 짝꿍이 몇 쌍 존재하는지 구하여 return 하도록 solution 함수를 완성해주세요.

제한 사항

• 2 ≤ weights의 길이 ≤ 100,000
• 100 ≤ weights[i] ≤ 1,000
• 몸무게 단위는 N(뉴턴)으로 주어집니다.
• 몸무게는 모두 정수입니다.

입출력 예

입출력 예 설명

• {100, 100} 은 서로 같은 거리에 마주보고 앉으면 균형을 이룹니다.
• {180, 360} 은 각각 4(m), 2(m) 거리에 마주보고 앉으면 균형을 이룹니다.
• {180, 270} 은 각각 3(m), 2(m) 거리에 마주보고 앉으면 균형을 이룹니다.
• {270, 360} 은 각각 4(m), 3(m) 거리에 마주보고 앉으면 균형을 이룹니다.

풀이

설계

1. 다음의 몸무게 비율을 갖는 두 사람은 시소 짝궁이 될 수 있다.
   • 1:1(2:2) / 1:2(2:4) / 2:3 / 3:4
   • 1번째 좌석이 없으므로 1:3, 1:4 비율은 설정할 수 없다.
   • 즉, 몸무게 w에 대하여, w, 2w, 1/2w, 2/3w, 3/2w, 3/4w, 4/3w의 몸무게에 해당하는 사람과 시소 짝궁이 된다.
2. 딕셔너리를 생성해 각 사람별로 자신과 짝을 이룰 수 있는 몸무게를 answer에 더하고, 자신의 몸무게를 키 값으로 하는 딕셔너리에 1을 추가한다.
   • 첫 번째 사람은 아무와도 짝을 이룰 수 없지만, 자신을 딕셔너리에 추가함으로써 이후 사람과 짝이 될 수 있는 가능성을 남겨 둔다.
   • collections의 defaultdict를 사용하여 '딕셔너리 내에 존재하지 않는 키'에 대한 기본값을 설정할 수 있다.

코드

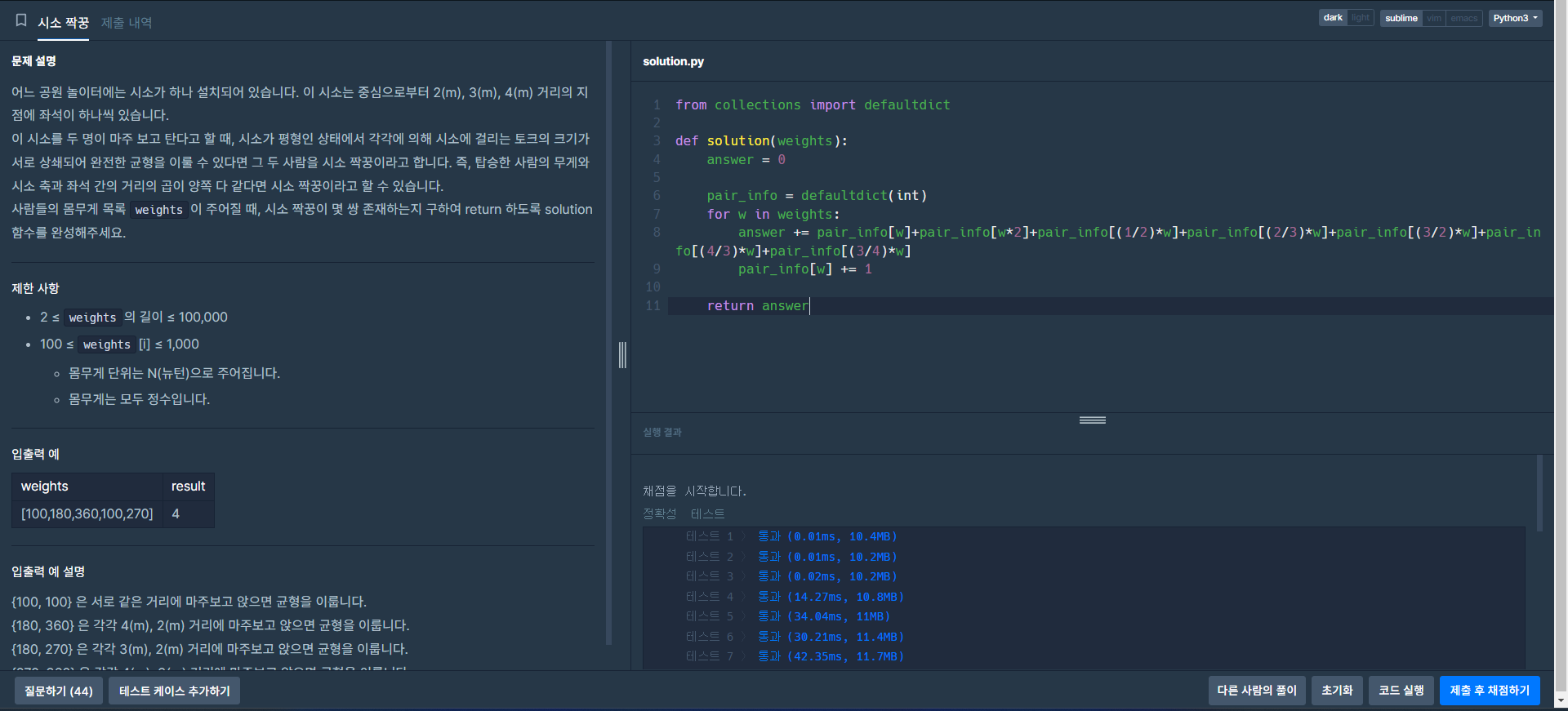
from collections import defaultdict

def solution(weights):
    answer = 0
    
    pair_info = defaultdict(int)
    for w in weights:
        answer += pair_info[w]+pair_info[w*2]+pair_info[(1/2)*w]+pair_info[(2/3)*w]+pair_info[(3/2)*w]+pair_info[(4/3)*w]+pair_info[(3/4)*w]
        pair_info[w] += 1

    return answer