
이해가 안가서 다시 보고 이해하기 ㅎㅎ
일단, 퍼셉트론을 복습하며 퍼셉트론의 동작을 식으로 나타내보았다.
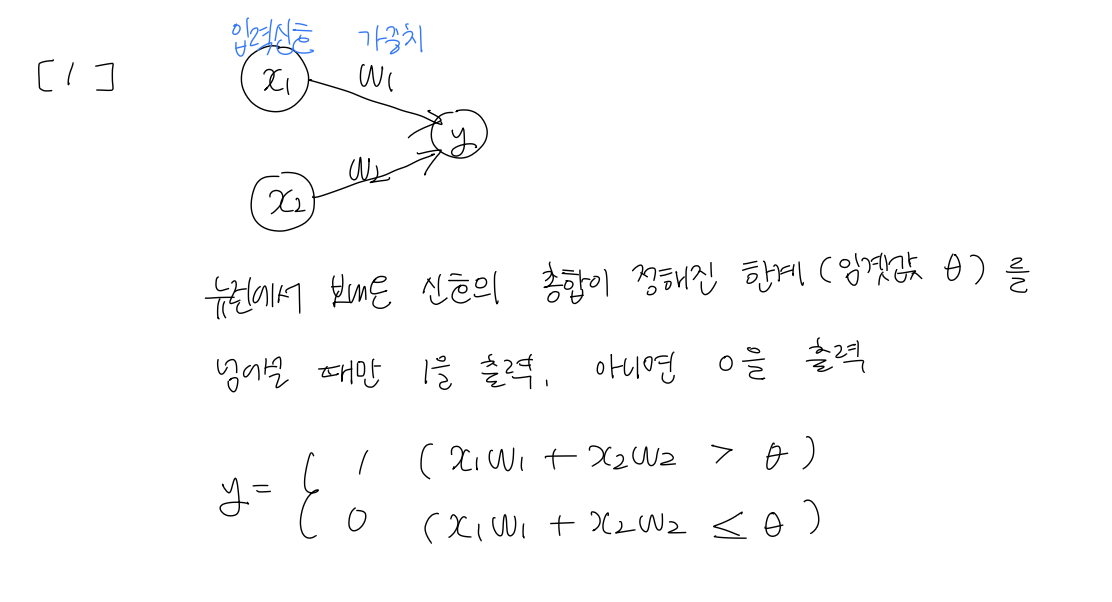
여기서 임곗값을 b(편향)를 사용해 치환해 다시 나타내면,
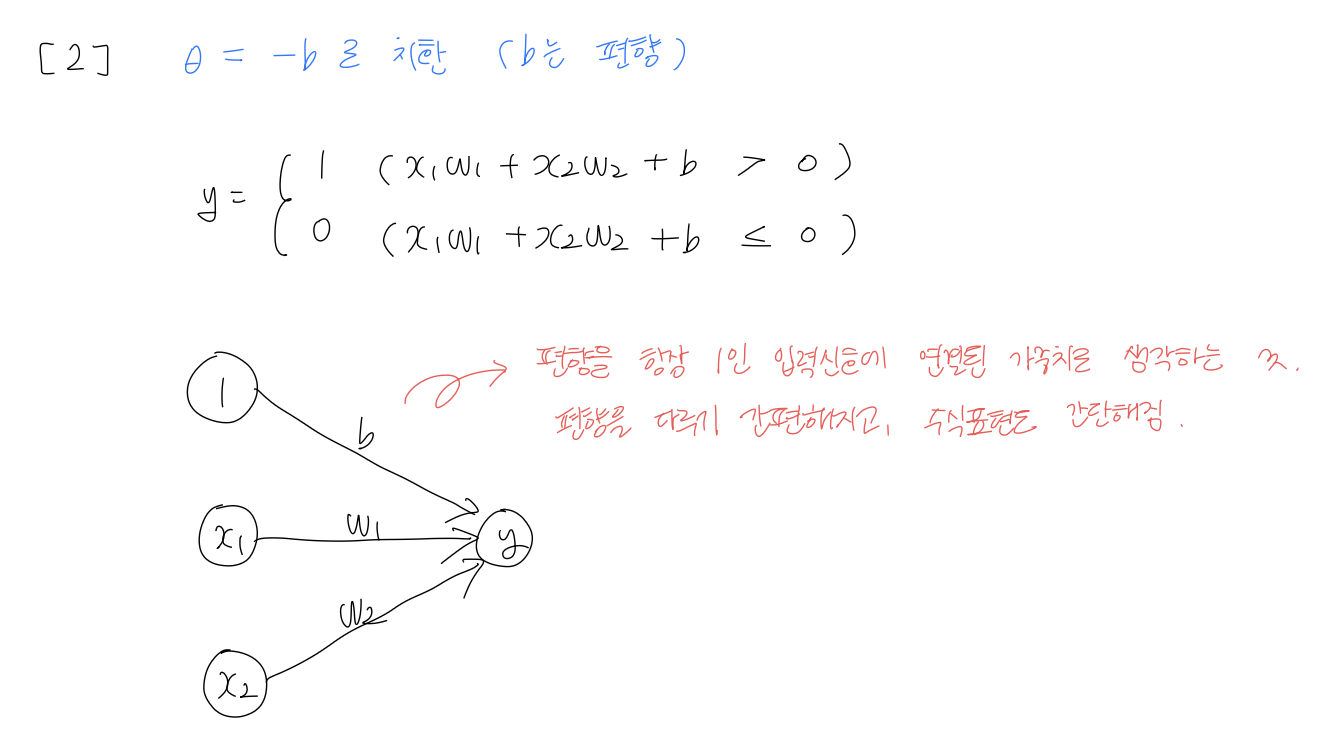
식을 x로 정리해 나타내면,
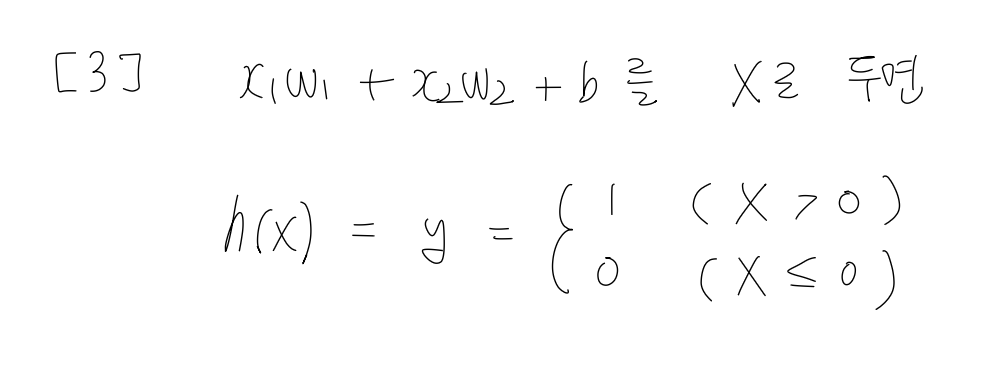
일단, 여기까지 보고 신경망에 대해서 다시 한번 살펴보자.
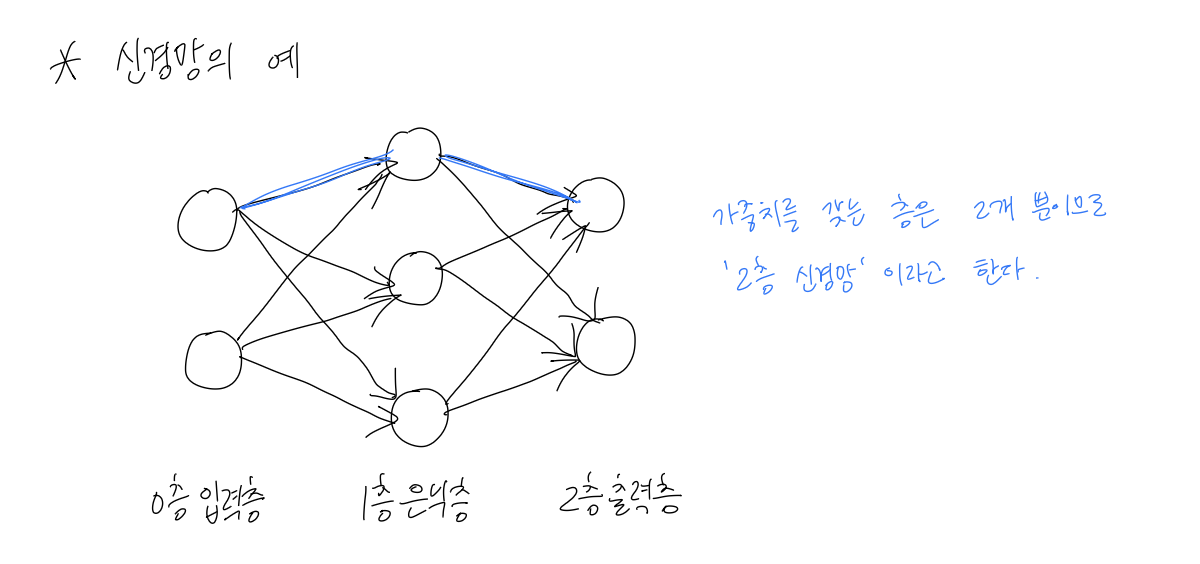
위 그림에서 볼 수 있듯이 신경망은 입력 > 은닉층 > 출력으로 연결되 수많은 뉴런(노드)들의 집합이다.
각 뉴런은 입력 * 가중치 + 편향 연산을 해서 선형의 결과(숫자)를 만든다.
그런데 이렇게만 계산한다면 아무리 층을 쌓아도 선형 함수를 이용한 결과만 나오게 된다.


그래서 활성화 함수가 필요한 것이다.
뉴런이 만든 결과값에 비선형 변환을 주는 것
즉, 신경망이 곡선이나 복잡한 경계를 학습할 수 있게 되는 것이다.
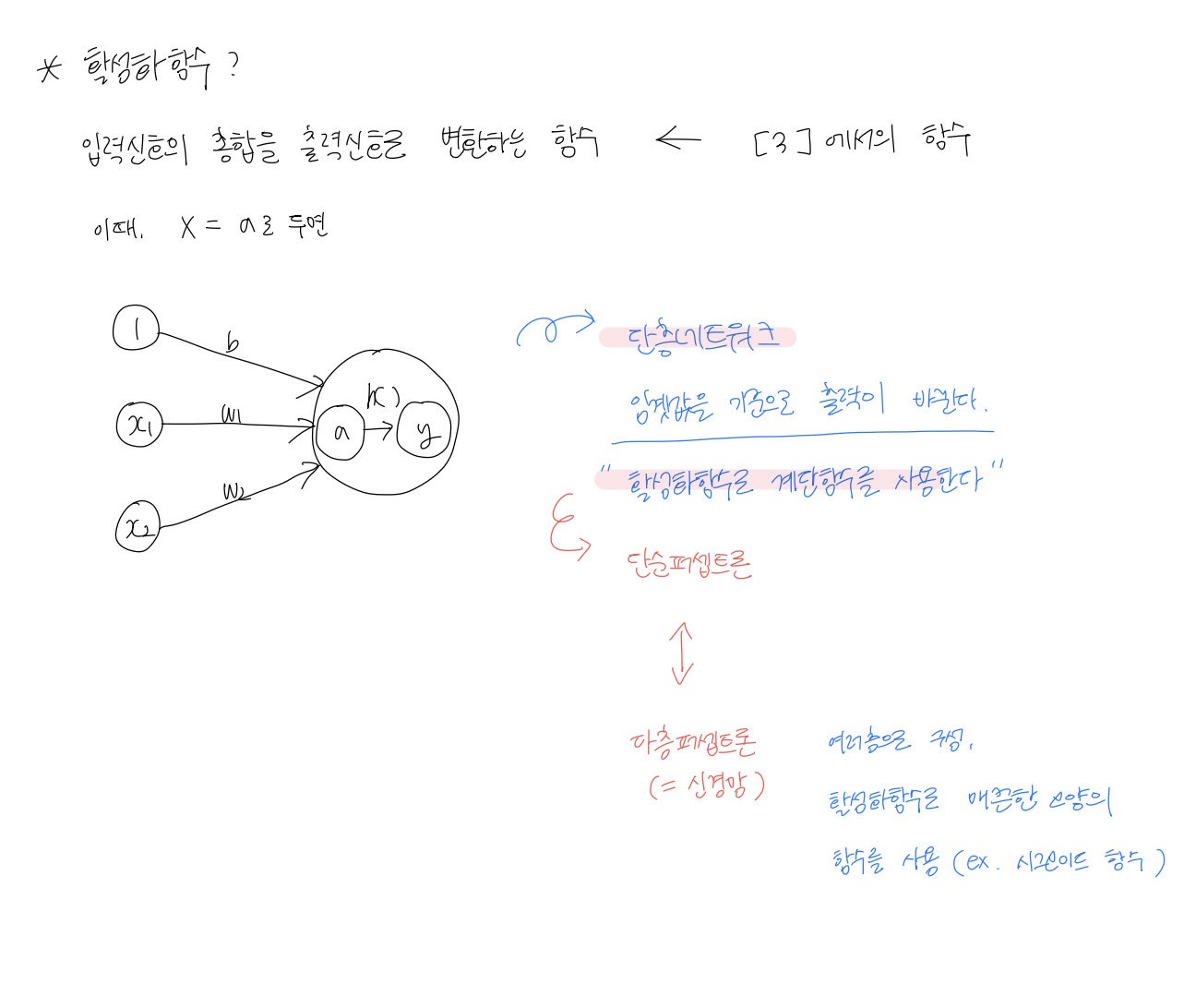
단순퍼셉트론 vs 다층퍼셉트론
단층 퍼셉트론은 단층 네트워크로, 입력>출력이 바로 연결된 네트워크이다. 임곗값을 기준으로 출력이 바뀌는 단순한 분류기라서 복잡한 문제를 풀 수 없다. 그래서 신경망이라고 부르지 않음 (그냥 논리 회로 기계에 가까움)
입력이 많아지면 수식이 복잡해질 수 는 있지만, 결과는 결국 하나의 직선으로 공간을 나누는 것 밖에 못한다.
직선으로 나눌 수 없는 문제는 못품
다층 퍼셉트론은 여러 층으로 이루어져있고, 활성화 함수로 시그모이드 함수 같은 매끈한 모양의 함수를 사용한다. 은닉층과 비선형 함수가 들어가면서 다양한 패턴을 학습할 수 있어 복잡한 문제를 풀 수 있음. 그래서 신경망이라고 부름
은닉층에서 비선형 활성화 함수가 들어가기 때문에, 선형 만으로는 못풀던 문제를 풀 수 있다. 여러 층을 거치면서 곡선, 꺾인 경계, 복잡한 패턴까지 표현이 가능해져 어려운 문제를 풀 수 있다.
계단함수, 시그모이드함수, 렐루함수
- 계단함수
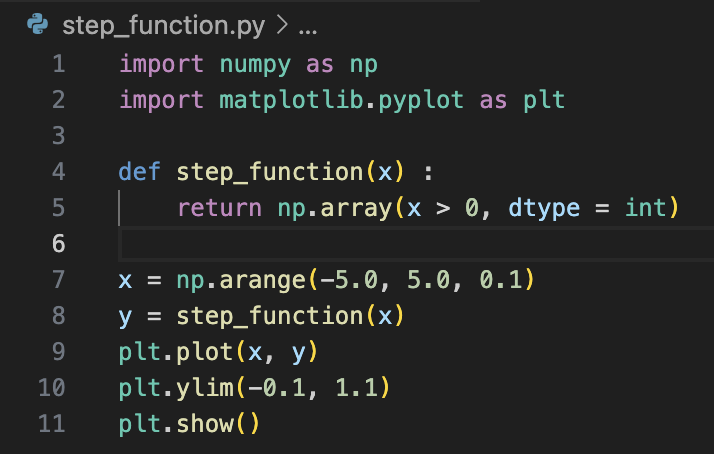
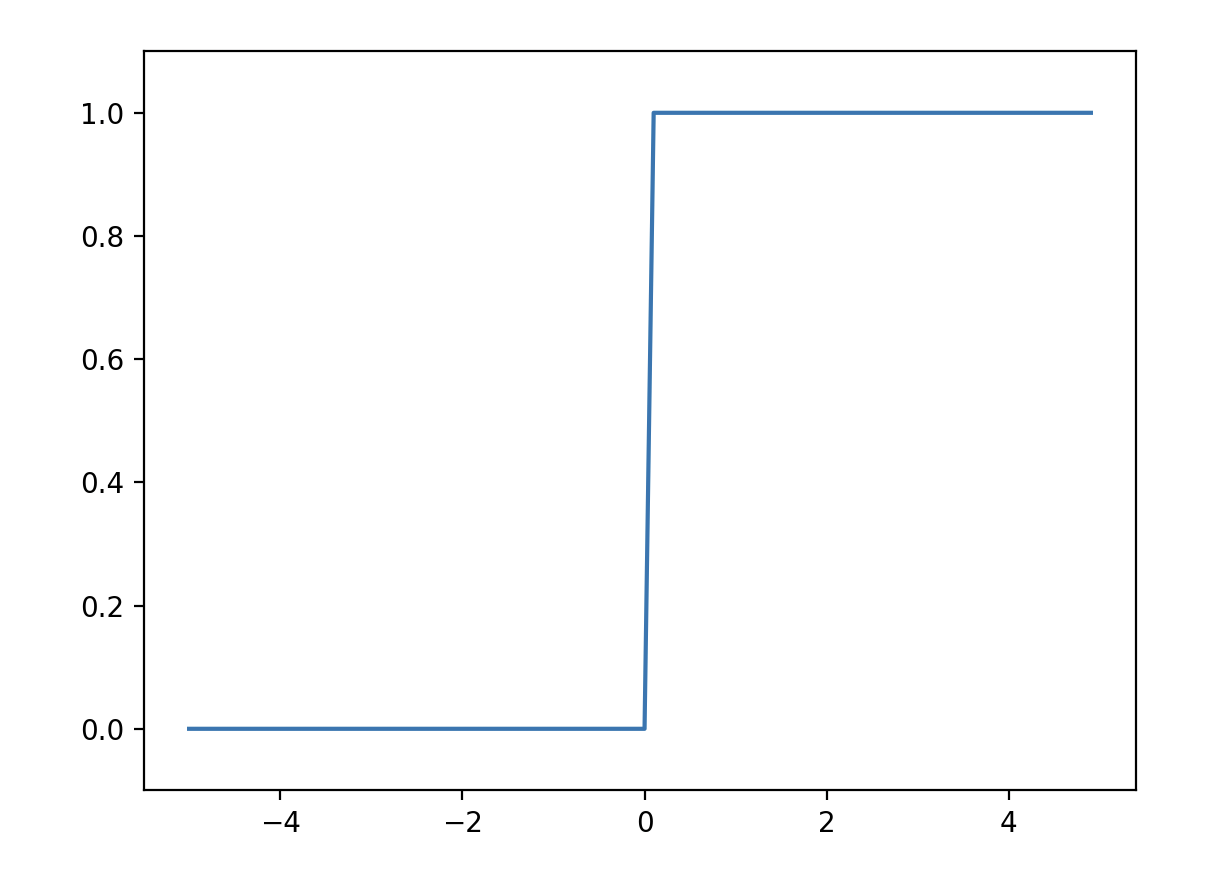
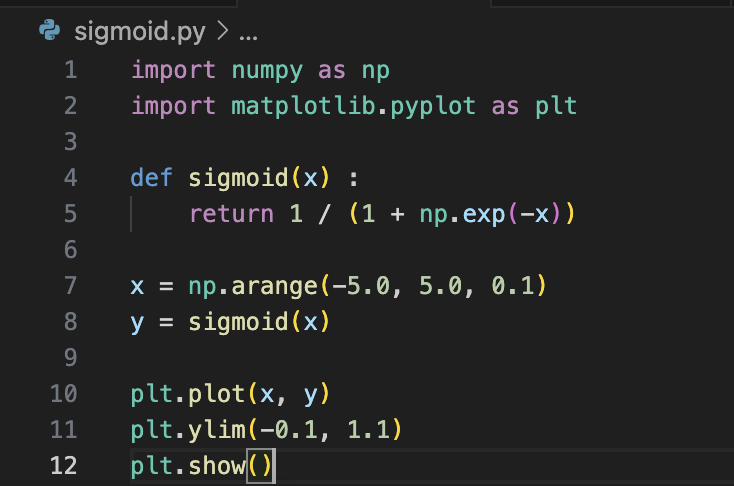
- 시그모이드 함수
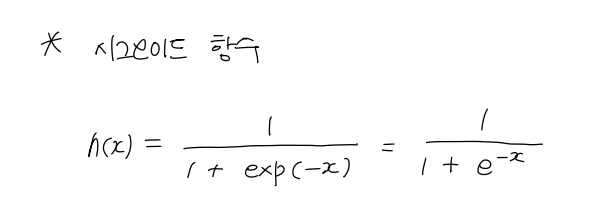
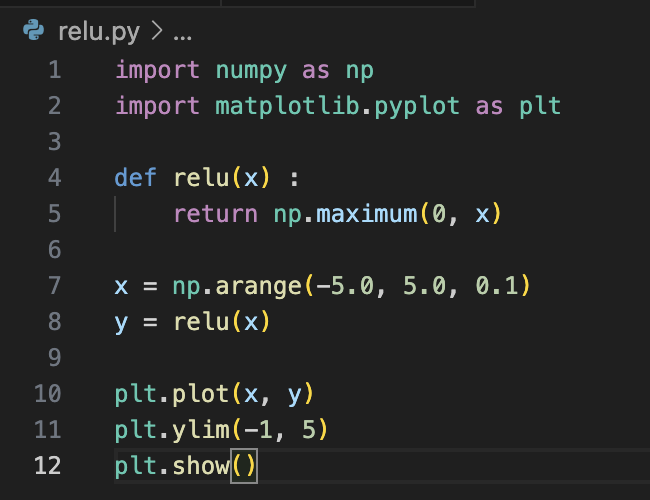
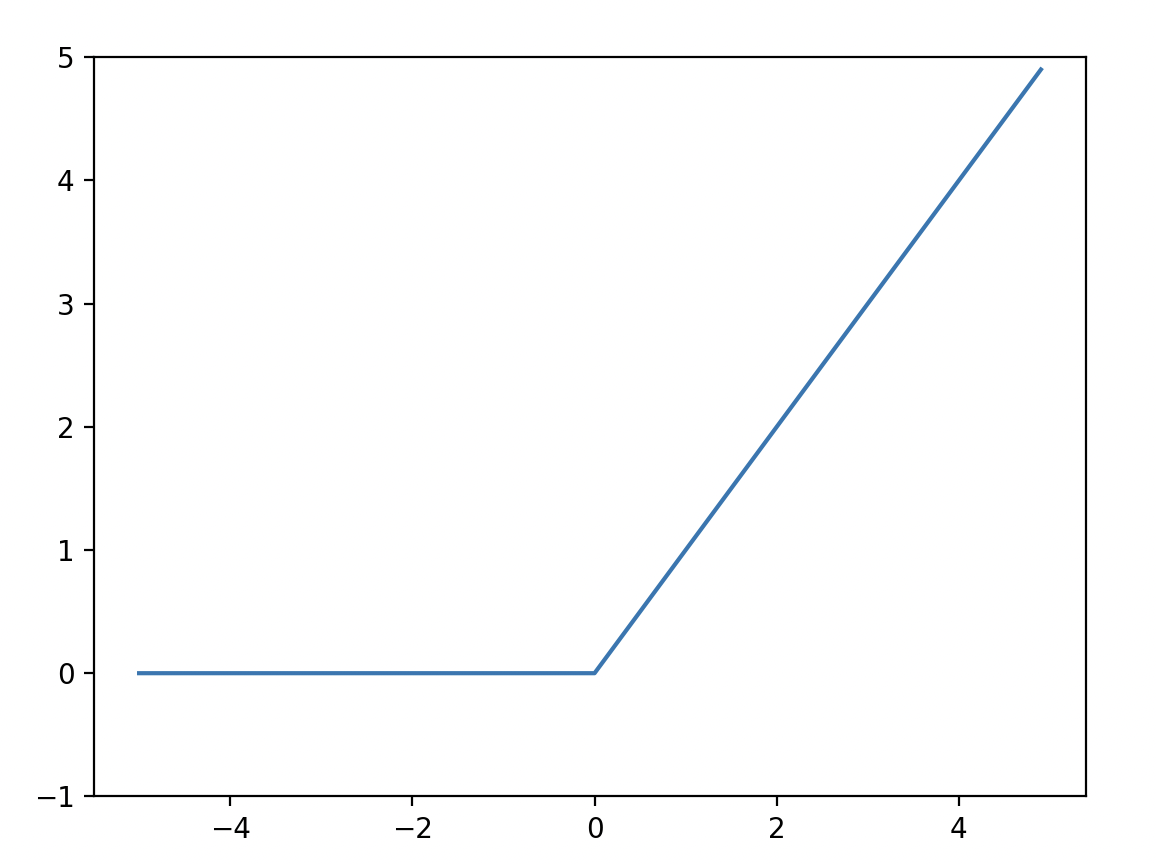
- 렐루 함수



잘보고갑니다.