[LeetCode] 1293. Shortest Path in a Grid with Obstacles Elimination

김민우·2022년 10월 30일

알고리즘

목록 보기

56/189

- Problem

1293. Shortest Path in a Grid with Obstacles Elimination
You are given an m x n integer matrix grid where each cell is either 0 (empty) or 1 (obstacle). You can move up, down, left, or right from and to an empty cell in one step.

Return the minimum number of steps to walk from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1) given that you can eliminate at most k obstacles. If it is not possible to find such walk return -1.

좌표 (0, 0)에서 출발하여 목적지 (m-1, n-1)까지 이동하는 데 가장 짧은 거리를 리턴해야 한다. 만약에 도달할 수 없을 경우 -1을 리턴한다.

이동은 이동하려는 좌표의 값이 0일 때 즉, grid[x][y] = 0일 때 이동할 수 있으나, 벽(grid[x][y] = 1)을 깨부수고 이동할 수도 있다.

벽을 깰 수 있는 횟수는 k로 주어진다.

Example 1:

Input: grid = [[0,0,0],[1,1,0],[0,0,0],[0,1,1],[0,0,0]], k = 1
Output: 6
Explanation: 
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> (3,2) -> (4,2).

Example 2:

Input: grid = [[0,1,1],[1,1,1],[1,0,0]], k = 1
Output: -1
Explanation: We need to eliminate at least two obstacles to find such a walk.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 40
1 <= k <= m * n
grid[i][j] is either 0 or 1.
grid[0][0] == grid[m - 1][n - 1] == 0

- 내 풀이 1 (오답)

class Solution:    
    def shortestPath(self, grid: List[List[int]], k: int) -> int:
        M, N = len(grid), len(grid[0])
        if M == 1 and N == 1:
            return 0
        
        q = collections.deque([[0, 0, 0, k]])
        grid[0][0] = -1

        while q:
            x, y, c, r = q.popleft()

            for dx, dy in ((-1, 0), (1, 0), (0, -1), (0, 1)):
                nx, ny = x + dx, y + dy

                if 0 <= nx < M and 0 <= ny < N:
                    if grid[nx][ny] == 0:
                        if nx == M-1 and ny == N-1:
                            return c+1
                        grid[nx][ny] = -1
                        q.append([nx, ny, c+1, r])   
                        
                    if grid[nx][ny] == 1 and r:
                        grid[nx][ny] = -1
                        q.append([nx, ny, c+1, r-1])
                
        return -1

가장 빨리 도달할 수 있는 최단 경로를 찾기에 bfs를 사용하여 탐색을 진행한다.
queue에 벽을 깨부술 수 있는 횟수 k를 담는다.
- q에 담기는 값은 다음과 같다.
x = row, y = column, c = steps, r = elimination count
이동할 수 있는 경로는 0 혹은 1(k>0)이다. 이미 이동한 경로라면 해당 좌표의 값을 -1로 바꾸어 이동할 수 없게 만든다.

- 결과

52개의 테스트 케이스 중 48개 성공, 4개가 실패이다.
막힌 케이스는 다음과 같다
grid = [[0,0],[1,0],[1,0],[1,0],[1,0],[1,0],[0,0],[0,1],[0,1],[0,1],[0,0],[1,0],[1,0],[0,0]] , k = 4
최단 경로 14가 나와야 정상이지만 위의 코드로는 16이 나온다.
그림으로 보자면,

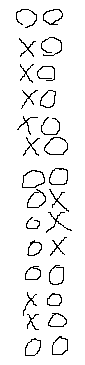
~~수준 무엇~~
이런 맵을 갖는다.

이러한 경로로 이동을 한다면 14번 만에 이동할 수 있다.

명확한 해답은 떠오르진 않지만, 하나 의심이 드는 것은 이미 지나간 경로를 또 지나가는 경우도 있을 것이다.

- 내 풀이 2

class Solution:    
    def shortestPath(self, grid: List[List[int]], k: int) -> int:
        M, N = len(grid), len(grid[0])        
        q = collections.deque([[0, 0, 0, k]])
        visited = set()
        
        while q:
            x, y, c, r = q.popleft()
            if x == M-1 and y == N-1:
                return c

            for nx, ny in ((x-1, y), (x+1, y), (x, y-1), (x, y+1)):
                if 0 <= nx < M and 0 <= ny < N:
                    if grid[nx][ny] == 0 and (nx, ny, r) not in visited:
                        visited.add((nx, ny, r))
                        q.append([nx, ny, c+1, r])   
                        
                    elif grid[nx][ny] == 1 and r and (nx, ny, r-1) not in visited:
                        visited.add((nx, ny, r-1))
                        q.append([nx, ny, c+1, r-1])
                
        return -1