[LeetCode] 2033. Minimum Operations to Make a Uni-Value Grid

- Problem

2033. Minimum Operations to Make a Uni-Value Grid

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

Example 1

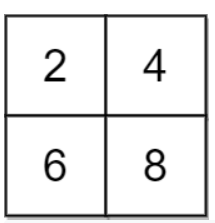
Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
  - Add x to 2 once.
  - Subtract x from 6 once.
  - Subtract x from 8 twice.
A total of 4 operations were used.

주어진 grid의 모든 원소를 x만큼 더하거나 빼서, 모든 원소들을 하나의 숫자로 만들 수 있다고 가정할 때, (불가능하다면 -1을 리턴)
덧셈, 뺄셈 연산을 최소 몇 번 해야하는지 구해야한다.

이러한 유형을 처음 접했을 때는 멍청하게도 x : 모든 원소들의 합 / 원소들의 개수으로 만드는 문제인줄 알았으나... 전혀 아니다.
주어진 모든 원소들을 정렬해서 나열한 뒤, 중앙값 (arr[원소의 개수 // 2])으로 통일하는 것이다.

- 내 풀이

class Solution:
    def minOperations(self, grid: List[List[int]], x: int) -> int:
        array = []
        answer = 0
        for g in grid:
            array.extend(g)
        array.sort()
        
        N = len(array)
        
        mid = array[N//2]
        M = mid % x
        
        for i in array:
            if i % x != M:
                return -1
            answer += abs(mid - i) // x
        
        return answer

- 결과