[LeetCode] 419. Battleships in a Board

- Problem

419. Battleships in a Board

Given an m x n matrix board where each cell is a battleship 'X' or empty '.', return the number of the battleships on board.

Battleships can only be placed horizontally or vertically on board. In other words, they can only be made of the shape 1 x k (1 row, k columns) or k x 1 (k rows, 1 column), where k can be of any size. At least one horizontal or vertical cell separates between two battleships (i.e., there are no adjacent battleships).

Example 1:

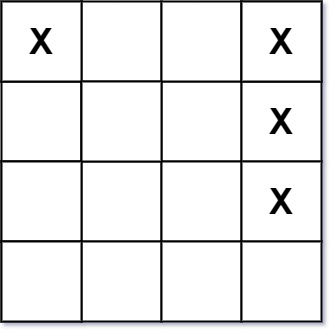
Input: board = [["X",".",".","X"],[".",".",".","X"],[".",".",".","X"]]
Output: 2

Example 2:

Input: board = [["."]]
Output: 0

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] is either '.' or 'X'.

Follow up: Could you do it in one-pass, using only O(1) extra memory and without modifying the values board?

그래프 탐색 기초문제라고 볼 수 있을 것 같다.

- 내 풀이

class Solution:
    def countBattleships(self, board: List[List[str]]) -> int:
        m, n = len(board), len(board[0])
        answer = 0
        
        def bfs(x, y):
            q = collections.deque([[x, y]])
            
            while q:
                x, y = q.popleft()
                
                for dx, dy in ((0, -1), (0, 1), (-1, 0), (1, 0)):
                    nx = x + dx
                    ny = y + dy
                    
                    if 0 <= nx < m and 0 <= ny < n and board[nx][ny] == "X":
                        q.append([nx, ny])
                        board[nx][ny] = "."
            
            return 1
        
        for i in range(m):
            for j in range(n):
                if board[i][j] == "X":
                    answer += bfs(i, j)
        
        return answer

        

추가 과제는 적용되지 않은 풀이이다.
O(1)의 추가 메모리를 사용하여 문제를 해결해야 하는데... 다음에 다시 풀어봐야지

- 결과