- Problem

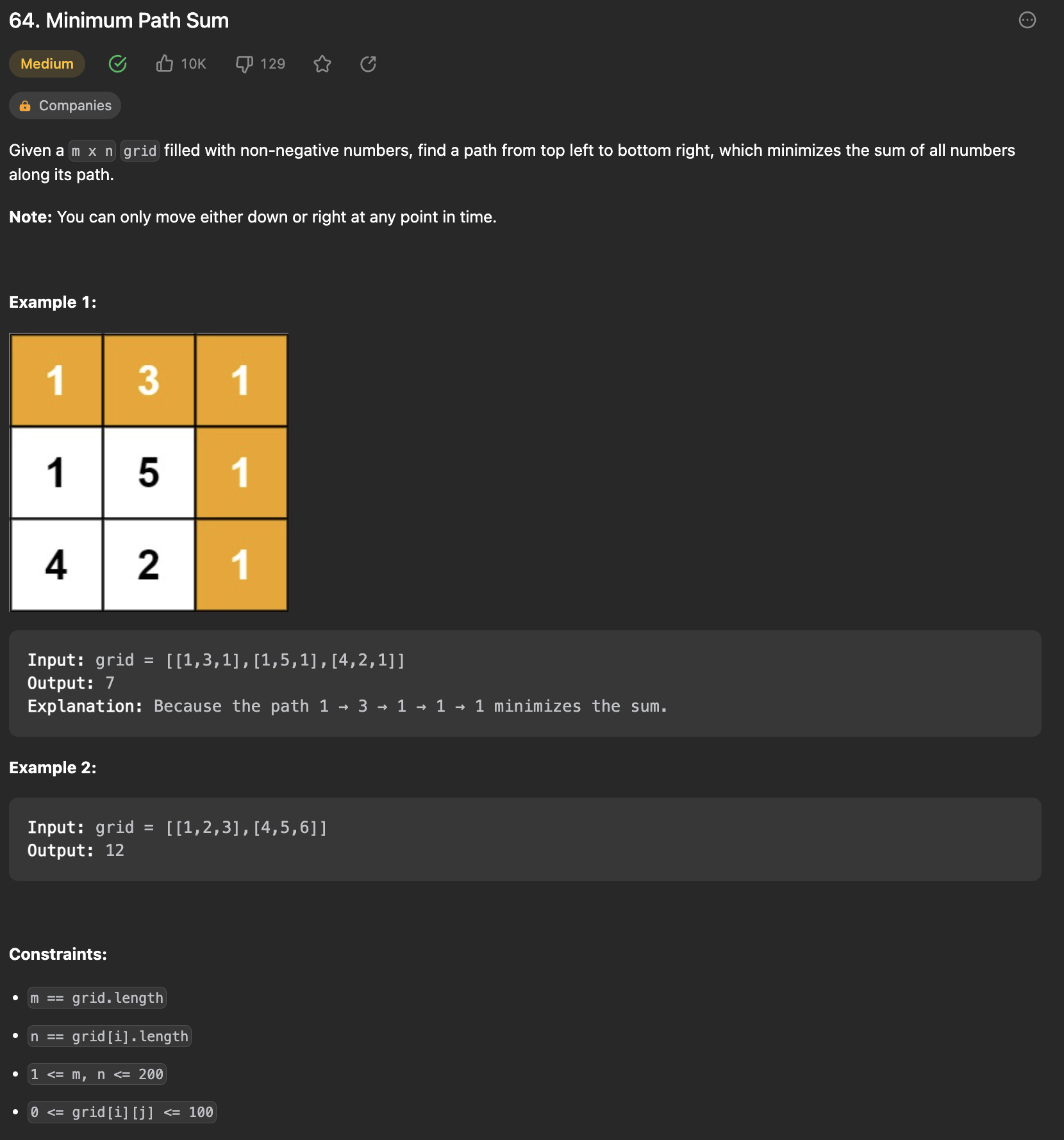
64. Minimum Path Sum

m * n 크기의 2차원 배열이 주어진다. (0, 0) 지점부터 (M-1, N-1) 지점까지 이동할 때 경로의 합이 최소가 되는 경우를 구해야 한다.
각 원소는 0 이상 100이하의 정수이며, 이동은 아래 또는 오른쪽으로만 가능하다.

- 내 풀이

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        M, N = len(grid), len(grid[0])
        dp = [[0 for _ in range(N+1)] for _ in range(M+1)]

        for i in range(M):
            for j in range(N):
                if i == 0:
                    dp[i+1][j+1] = grid[i][j] + dp[i+1][j]
                elif j == 0:
                    dp[i+1][j+1] = grid[i][j] + dp[i][j+1]
                else:
                    dp[i+1][j+1] = grid[i][j] + min(dp[i][j+1], dp[i+1][j])

        return dp[-1][-1]

- 결과

• 시간 복잡도: O(MN)
• 공간 복잡도: O(MN)

공간 복잡도를 더욱 최적화하여 풀 수 있는 방법도 있다.
중간 결과를 저장하기 위해 dp 테이블을 사용하지 않고, 원본 grid의 값을 변경하며 접근할 수 있다.
코드는 다음과 같다.

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        M, N = len(grid), len(grid[0])

        for j in range(1, N):
            grid[0][j] += grid[0][j-1]

        for i in range(1, M):
            grid[i][0] += grid[i-1][0]

        for i in range(1, M):
            for j in range(1, N):
                grid[i][j] += min(grid[i-1][j], grid[i][j-1])

        return grid[-1][-1]