[LeetCode] 73. Set Matrix Zeroes

- Problem

73. Set Matrix Zeroes

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's.

You must do it in place.

Example 1:

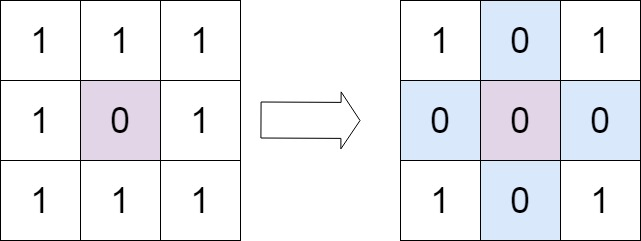
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

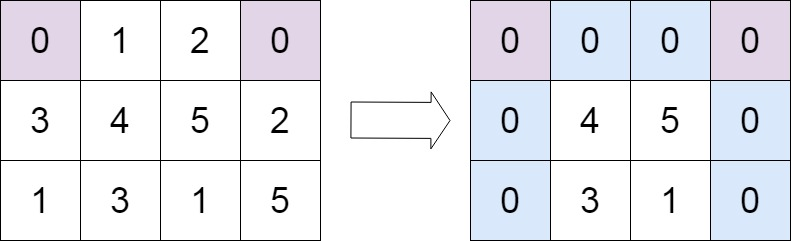
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -2^31 <= matrix[i][j] <= 2^31 - 1

Follow up:

• A straightforward solution using O(mn) space is probably a bad idea.
• A simple improvement uses O(m + n) space, but still not the best solution.
• Could you devise a constant space solution?

---

행렬 matrix가 주어질 때, 원소가 0이라면 해당 원소의 모든 행과 열을 0으로 바꾸는 문제이다.

- 내 풀이 1

우선 공간복잡도 O(M*N), 시간 복잡도 O(M+N)을 만족하는 코드이다.

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        row, col = set(), set()
        M, N = len(matrix), len(matrix[0])
        for i in range(M):
            for j in range(N):
                if matrix[i][j] == 0:
                    row.add(i)
                    col.add(j)
        
        for r in row:
            for i in range(N):
                matrix[r][i] = 0
        
        for c in col:
            for j in range(M):
                matrix[j][c] = 0

중복적으로 행열을 탐색하는 일을 방지하고자 set 자료형을 사용한다.
문제 풀이는 심플하다.

1. matrix를 하나씩 탐색하여 원소가 0이라면 해당 원소의 행을 row에 담고, 열을 col에 담는다.

2. row, col을 돌며, 해당하는 모든 행과 열을 0으로 바꾼다.

그러나, Follow up을 보면, 이 문제를 공간 복잡도가 O(1)인 풀이를 요구한다.

---

- 내 풀이 2

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        M, N = len(matrix), len(matrix[0])
        
        for i in range(M):
            for j in range(N):
                if matrix[i][j] == 0:
                    for k in range(N):
                        if matrix[i][k] != 0:
                            matrix[i][k] = "zero"
                    for l in range(M):
                        if matrix[l][j] != 0:
                            matrix[l][j] = "zero"
        
        for i in range(M):
            for j in range(N):
                if matrix[i][j] == "zero":
                    matrix[i][j] = 0

코드가 굉장히 더럽다.

우선, set 자료형을 사용하지 않는다. 행렬의 길이 M,N을 제외한 어떠한 추가적인 메모리도 소모하지 않는다. 따라서 공간 복잡도 O(1)을 만족한다.

행렬을 순회하며 0을 만날 경우, 0이 아닌 판별 가능한 임의의 다른 값(zero)으로 바꿔줘야 한다.

• 만약 바로 0으로 바꾼다면, 모든 원소가 0으로 바뀔 것이다.

- 결과