1. 큐(Queue)

1.1 큐(Queue) 란?

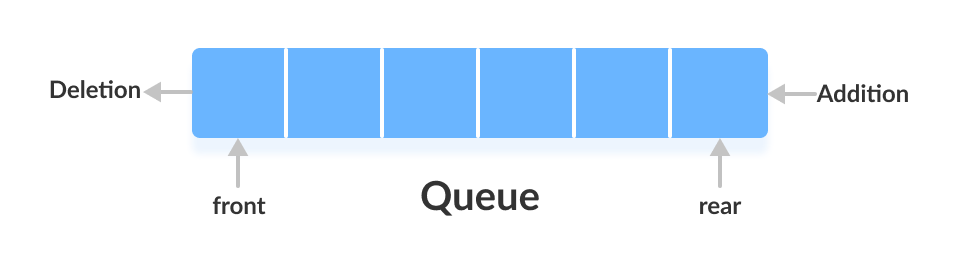
이와 같이 한쪽 끝에서 Data를 넣고 다른 한쪽에서 Data를 뺄 수 있는 구조이다.
즉, FIFO(First In First Out) 이다.

1.2 큐(Queue) 연산

push : 큐에 데이터를 넣는 연산
pop : 큐에서 데이터를 빼는 연산
front : 큐의 가장 앞에 있는 데이터를 보는 연산
back : 큐의 가장 뒤에 있는 데이터를 보는 연산
empty : 큐가 비어있는지 아닌지를 알아보는 연산
size : 큐에 저장되어있는 데이터의 갯수를 알아보는 연산

java.util.Queue 를 사용하는 것이 좋다.

1.3 큐 구현 백준 문제 : 큐

코드 1.

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int n = sc.nextInt();
	int[] queue = new int[n];
	int front = 0;
	int rear = 0;
	while (n-- > 0) {
		String s = sc.next();
		if (s.equals("push")) {
			int num = Integer.parseInt(sc.next());
			queue[rear++] = num;
		} else if (s.equals("front")) {
			if (front == rear) {
				System.out.println("-1");
			} else {
				System.out.println(queue[front]);
			}
		} else if (s.equals("size")) {
			System.out.println(rear - front);
		} else if (s.equals("empty")) {
			if (front == rear) {
				System.out.println("1");
			} else {
				System.out.println("0");
			}
		} else if (s.equals("pop")) {
			if (front == rear) {
				System.out.println("-1");
			} else {
				System.out.println(queue[front]);
				front += 1;
			}
		} else if (s.equals("back")) {
			if (front == rear) {
				System.out.println("-1");
			} else {
				System.out.println(queue[rear - 1]);
			}
		}
	}
}

코드 2.

자바 Queue 에는 back 연산이 없기 때문에 직접 구현해야한다.
push 연산을 할때마다 해당 값을 특정 변수에 저장해 놓으면 back 연산을 할 수 있다.

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int n = sc.nextInt();
	int last = 0;
	Queue<Integer> queue = new LinkedList<Integer>();
	for (int i = 0; i < n; i++) {
		String s = sc.next();
		if (s.equals("push")) {
			int num = Integer.parseInt(sc.next());
			last = num;
			queue.offer(num);
		} else if (s.equals("front")) {
			if (queue.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(queue.peek());
			}
		} else if (s.equals("size")) {
			System.out.println(queue.size());
		} else if (s.equals("empty")) {
			if (queue.isEmpty()) {
				System.out.println("1");
			} else {
				System.out.println("0");
			}
		} else if (s.equals("pop")) {
			if (queue.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(queue.poll());
			}
		} else if (s.equals("back")) {
			if (queue.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(last);
			}
		}
	}
}

자바 API Queue 에 들어가면 Queue에 대한 메서드들을 확인 할 수 있다.

1.4 문제 백준 문제 : 요세푸스 문제

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int n = sc.nextInt();
	int k = sc.nextInt();
	StringBuilder sb = new StringBuilder();
	sb.append("<");
	Queue<Integer> queue = new LinkedList<Integer>();
	for (int i = 1; i <= n; i++) {
		queue.offer(i);
	}
	for (int i = 0; i < n - 1; i++) {
		for (int j = 0; j < k - 1; j++) {
			queue.offer(queue.poll());
		}
		sb.append(queue.poll() + ", ");
	}
	sb.append(queue.poll() + ">");
	System.out.println(sb);
}

• k-1번째까지 데이터를 꺼내 다시 큐에 push를 한다.

2. 덱(Deque)

이와 같이 양 끝에서 데이터를 넣고 뺄 수 있는 구조이다.

2.1 덱(Deque) 연산

push_front : 덱의 앞에 데이터를 넣는 연산
push_back : 덱의 뒤에 데이터를 넣는 연산
pop_front : 덱의 앞에서 데이터를 빼는 연산
pop_back : 덱의 뒤에서 데이터를 빼는 연산
front : 덱의 가장 앞에 있는 데이터를 보는 연산
back : 덱의 가장 뒤에 있는 데이터를 보는 연산

2.2 덱(Deque) 구현 백준 문제 : 덱

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int n = sc.nextInt();
	sc.nextLine();
	ArrayDeque<Integer> adq = new ArrayDeque<Integer>();
	for (int i = 0; i < n; i++) {
		String str = sc.nextLine();
		String[] s = str.split(" ");
		String c = s[0];
		switch (c) {
		case "push_front":
			int num1 = Integer.parseInt(s[1]);
			adq.offerFirst(num1);
			break;
		case "push_back":
			int num2 = Integer.parseInt(s[1]);
			adq.offerLast(num2);
			break;
		case "front":
			if (adq.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(adq.peekFirst());
			}
			break;
		case "size":
			System.out.println(adq.size());
			break;
		case "empty":
			if (adq.isEmpty()) {
				System.out.println("1");
			} else {
				System.out.println("0");
			}
			break;
		case "pop_front":
			if (adq.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(adq.pollFirst());
			}
			break;
		case "pop_back":
			if (adq.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(adq.pollLast());
			}
			break;
		case "back":
			if (adq.isEmpty()) {
				System.out.println("-1");
			} else {
				System.out.println(adq.peekLast());
			}
			break;
		}
	}
}

3. 문제

3.1 문제1 백준 문제 : 단어 뒤집기 2

• 문자열이 입력으로 주어지면 태그를 제외한 단어를 뒤집는 문제이다.
• '<'를 기준으로 처음부터 '<'가 나올 수 있고 또는 단어가 나온 뒤 '<'가 나올 수 있다.
• 이러한 경우 '<' 이전에 단어는 출력을 해야한다.
• 또한 태그인지 판별하기 위해 boolean 변수를 사용한다.

즉, < abcd > 형태이면 '<'를 만나면 boolean변수를 true로 바뀌고, abcd는 스택에 넣지 않고 바로 출력한다.
이후 '>'일 때 boolean변수는 false로 바뀌게 된다.

태그부분을 제외한 나머지 단어는 스택에 넣어 출력한다.

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	String str = sc.nextLine();
	boolean tag = false;
	Stack<Character> s = new Stack<Character>();
	for (char ch : str.toCharArray()) {
		if (ch == '<') {
			print(s);
			tag = true;
			System.out.print(ch);
		} else if (ch == '>') {
			tag = false;
			System.out.print(ch);
		} else if (tag) {
			System.out.print(ch);
		} else {
			if (ch == ' ') {
				print(s);
				System.out.print(ch);
			} else {
				s.push(ch);
			}
		}
	}
	print(s);
	System.out.println("\n");
}
public static void print(Stack<Character> s) {
	while (!s.isEmpty()) {
		System.out.print(s.pop());
	}
}

3.2 문제2 백준 문제 : 쇠막대기

• 괄호 문자열 문제와 유사하다.
• '( )' 는 쇠막대기 또는 레이저를 의미
• 인접한 ( ) 일 경우 레이저이다. 즉, '(' 와 ')' 인덱스 차이는 1이다.
• 또한 레이저 하나로 쇠막대기를 두개로 나눌수 있다.
• 해당 문제에 요점은 ')'가 나왔을 때 이것이 쇠막대기의 끝을 의미하는지, 레이저를 의미하는지 판단해야 한다.

예를들면,
(()()) 이런식으로 주어졌다 가정하면 쇠막대기 하나이고 레이저가 2개인 것이다. 결과는 3등분으로 나뉘는 것

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	String str = sc.nextLine();
	Stack<Integer> s = new Stack<Integer>();
	int cnt = 0;
	for(int i=0; i<str.length(); i++) {
		char c = str.charAt(i);
		if(c == '(') {
			s.push(i);
		}else {
			if(s.peek()+1 == i) { // 레이저에 해당
				s.pop();
				cnt += s.size();
			}else { // 쇠 막대기의 끝을 의미
				s.pop();
				cnt+=1;
			}
		}
	}
	System.out.println(cnt);
}

3.3 문제3 백준 문제 : 오큰수

• 오큰수란?
  임의의 원소인 $A_i$의 오른쪽에 있으면서 $A_i$보다 큰 수 중 제일 왼쪽에 있는 수를 의미한다.
• 해당 문제는 주어진 배열에서 해당 값의 오큰수를 구하는 문제이다.
• 예를들어 A = [3,5,2,7] 인 경우 3의 오큰수는 5이다.
• 임의의 수의 오큰수가 $A_j$ 이라면, 자기자신과 $A_j$ 사이에는 자신보다 큰 수가 없다는 성질이 존재한다.
  즉, [5 3 7] 일 때 5의 오큰수는 7이며 중간에 5보다 큰 수는 없다.
• 모든 과정이 끝나고 스택에 아직 값이 남아있으면 이는 오큰수가 존재하지 않다는 것이다.

public static void main(String[] args) throws IOException {
	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	int n = Integer.parseInt(br.readLine());
	int[] a = new int[n]; //수열 A
	int[] result = new int[n]; // 결과
	String[] strNum = br.readLine().split(" ");
	for(int i=0;i<n;i++) {
		a[i] = Integer.parseInt(strNum[i]);
	}
	Stack<Integer> s = new Stack<Integer>();
	for(int i=0; i<n; i++) {
		if(s.isEmpty()) { // 처음 값을 넣게 되는 경우
			s.push(i);
		}
		while(!s.isEmpty() && a[s.peek()] < a[i]) { // 오큰수
			result[s.pop()] = a[i];
		}
		s.push(i); // 스택의 제일 높이 있는 값보다 작은경우 스택에 push
	}
	while(!s.empty()) { // 오큰수를 찾지 못한 값들이 스택에 남아 있는 경우
		result[s.pop()] = -1;
	}
	BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
	for(int i=0;i<n;i++) {
		bw.write(result[i] + " ");
	}
	bw.write("\n");
	bw.flush();
}

해당 문제를 처음에 Scanner 를 이용하여 구현해봤으나 시간초과 문제가 발생하였다.
BufferedReader 와 BufferedWriter 를 이용하여 구현해야한다.

3.4 문제4 백준 문제 : 오큰등수

• 오큰등수는 오큰수 문제와 유사하다.
• 오큰등수는 임의의 원소 $A_i$에 오른쪽에 있으면서 $A_i$의 등장한 횟수보다 크면서 가장 왼쪽에 있는 수를 의미한다.
• 즉, 횟수를 비요하는 방식으로 문제를 해결하면 된다.

public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		int[] a = new int[n]; //수열 A
		int[] result = new int[n]; // 결과
		int[] freq = new int[1000001];
		String[] strNum = br.readLine().split(" ");
		for(int i=0;i<n;i++) {
			a[i] = Integer.parseInt(strNum[i]);
			freq[a[i]] += 1;
		}
		Stack<Integer> s = new Stack<Integer>();
		for(int i=0; i<n; i++) {
			if(s.isEmpty()) { // 처음 값을 넣게 되는 경우
				s.push(i);
			}
			while(!s.isEmpty() && freq[a[s.peek()]] < freq[a[i]]) { // 오큰등수
				result[s.pop()] = a[i];
			}
			s.push(i); // 스택의 제일 높이 있는 값보다 작은경우 스택에 push
		}
		while(!s.empty()) { // 오큰수를 찾지 못한 값들이 스택에 남아 있는 경우
			result[s.pop()] = -1;
		}
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		for(int i=0;i<n;i++) {
			bw.write(result[i] + " ");
		}
		bw.write("\n");
		bw.flush();
	}

참고

백준 알고리즘 기초 강의를 듣고 공부하기 위해 정리한 것입니다.