[Codility] Lesson 6 - NumberOfDiscIntersections

Task discription

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

A[0] = 1
A[1] = 5
A[2] = 2
A[3] = 1
A[4] = 4
A[5] = 0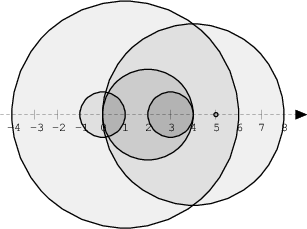

There are eleven (unordered) pairs of discs that intersect, namely:

• discs 1 and 4 intersect, and both intersect with all the other discs;
• disc 2 also intersects with discs 0 and 3.

Write a function:

int solution(vector<int> &A);

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Given array A shown above, the function should return 11, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..100,000];
• each element of array A is an integer within the range [0..2,147,483,647].

Source code

#include <algorithm>

int solution(vector<int> &A) {
    vector<long long> lower, upper;
    int n = A.size();
    // 각 디스크의 시작, 끝 구하기
    for(int i=0;i<n;i++) {
        lower.push_back((long long) i-A[i]);
        upper.push_back((long long) i+A[i]);
    }
    sort(lower.begin(), lower.end());

    int cnt = 0;
    for(int i=0;i<n-1;i++) {
        for(int j=i+1;j<n;j++) {
            if(cnt > 10000000)
            	return -1;
            // 디스크가 아예 교차하지 않으면 break
            if(lower[j] > upper[i])
            	break;
            // lower 기준 디스크 교차 여부 체크
            if(lower[j] >= lower[i] && lower[j] <= upper[i]) 
            	cnt++;
        }
    }
    return cnt;
}

Review

1. lower와 upper를 기준으로 문제를 해결하려 했더니 시간초과 에러가 발생했다.
   lower를 정렬한 후 디스크 교차 여부를 체크하는 방식으로 변경해야 시간복잡도가 O(N*log(N)) or O(N)가 되어 통과할 수 있다.
2. overflow 에러가 발생해 lower과 upper를 long long 타입으로 처리해주어야 했다.