백준 10159 - 저울

문제

https://www.acmicpc.net/problem/10159

리뷰

플로이드 워셜을 통해 쉽게 풀이할 수 있는 문제였다.

주어진 예제 그래프를 먼저 앞 정점 $\rightarrow$ 뒤 정점 방향의 그래프로 표현하면
형태가 아래 그림과 같다.

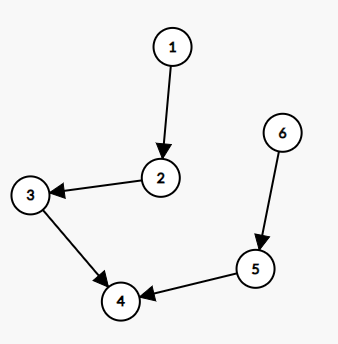
주어진 그래프의 각 정점에서 해당 정점으로 진입 가능한 정점, 해당 정점에서 진출 가능한
정점을 정리해보면 아래와 같다.

• 1 : 2
• 2 : 1(진입) / 3, 4(진출)
• 3 : 1, 2 / 4
• 4 : 1, 2, 3, 5, 6 (전부 진입)
• 5 : 6 / 4
• 6 : 5 (진출)

결국 특정 정점에서 해당 정점으로 진입 가능/해당 정점에서 진출 가능한 정점들이 아닌
정점들을 카운팅해주면 답을 도출할 수 있다.

위 아이디어에 따라 로직을 구성하기 위해 일단 간선의 비용을 전부 1로 설정하였다.
이후, 플로이드 워셜을 통해 모든 정점간 경로를 구한 다음 특정 정점 $i$에서 다른 정점 $j$가
있을때 map[i][j]와 map[j][i]가 둘 다 존재하지 않는 경우(==Integer.MAX_VALUE)만
카운팅하여 출력한다.

로직의 시간복잡도는 플로이드 워셜의 복잡도인 $O(N^3)$으로 수렴하고 이는 $N=100$인
최악의 경우에도 무난히 제한 조건 1초를 통과한다.

코드

import java.io.*;
import java.util.StringTokenizer;


import static java.lang.Integer.*;

public class Main {
    static int N;
    static int[][] map;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = parseInt(br.readLine());
        map = new int[N + 1][N + 1];
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++) {
                if (i == j) continue;

                map[i][j] = MAX_VALUE;
            }

        int M = parseInt(br.readLine());
        int i, j;
        StringTokenizer st;
        while (M-- > 0) {
            st = new StringTokenizer(br.readLine());
            i = parseInt(st.nextToken());
            j = parseInt(st.nextToken());

            map[i][j] = 1;
        }

        floyd();
        StringBuilder sb = new StringBuilder();
        for (i = 1; i <= N; i++) {
            int count = 0;

            for (j = 1; j <= N; j++) {
                if (i == j) continue;

                if (map[i][j] != MAX_VALUE || map[j][i] != MAX_VALUE)
                    continue;

                count++;
            }

            sb.append(count).append("\n");
        }
        System.out.print(sb);
        br.close();
    }

    static void floyd() {
        for (int k = 1; k <= N; k++)
            for (int i = 1; i <= N; i++)
                for (int j = 1; j <= N; j++) {
                    if (map[i][k] == MAX_VALUE || map[k][j] == MAX_VALUE)
                        continue;

                    map[i][j] = Math.min(map[i][j], map[i][k] + map[k][j]);
                }
    }
}

결과