백준 1185 - 유럽여행

문제

https://www.acmicpc.net/problem/1185

리뷰

크루스칼을 이용해 풀이할 수 있는 문제였다.

처음 이 문제를 풀이할 당시, 크루스칼을 이용해 MST를 형성하고 해당 MST를
그래프 탐색 내지는 다익스트라를 통해 비용을 도출하여 답을 구하는 접근으로
로직을 구성하려 하였다. 하지만, 로직적으로 비용이 중복 계산되거나 하는 문제가
존재하여 다른 접근을 생각해보아야 했다.

그러다 떠올린 것이 간선의 비용에 애초에 방문 비용을 포함시키는 발상이었다.
아래 그래프를 보자.

위 형태의 그래프가 존재할때 각 정점을 연결하는 간선은 유일하고, 이에 따라
만약 $A \rightarrow C$ 까지 탐색을 진행하고, $C \rightarrow A$ 로 다시
돌아온다고 한다면, 시작점은 무조건 2번 방문하게 되고 중간 정점은 경우에 따라
2번 방문하게 된다.

따라서 (A, B) 간선 비용 = A 방문 비용 + B 방문 비용 + 원래 간선 비용 x 2로
설정을 해주면

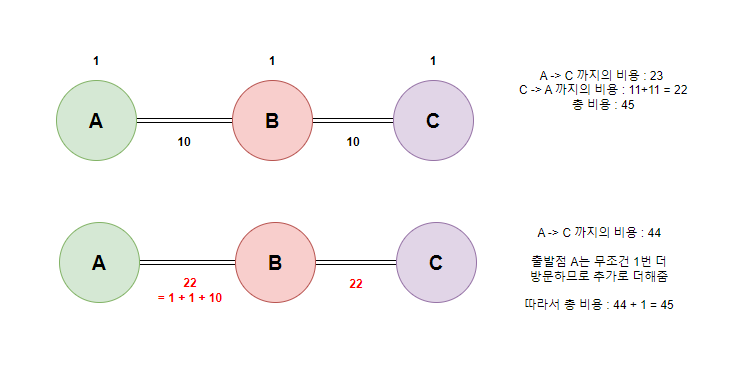
크루스칼을 이용해 MST를 구성하며 비용 합을 구했을 때, 중복하여 방문하는 정점의
방문 비용을 포함시켜 계산할 수 있는 형태로 로직을 구성할 수 있다.

로직의 시간복잡도는 크루스칼에서 $O(NlogP)$로 수렴하고 이는 $N=10,000$,
$P=100,000$인 최악의 경우에도 무난히 2초의 제한 조건을 통과할 수 있다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

import static java.lang.Integer.*;

public class Main {
    static int[] parent;
    static PriorityQueue<Edge> pq = new PriorityQueue<>(Comparator.comparingInt(e -> e.w));

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = parseInt(st.nextToken());
        int P = parseInt(st.nextToken());
        parent = new int[N + 1];

        int[] visitCost = new int[N + 1];
        int start = 1, minCost = 1001;
        for (int i = 1; i < visitCost.length; i++) {
            visitCost[i] = parseInt(br.readLine());

            if (minCost < visitCost[i]) continue;

            minCost = visitCost[i];
            start = i;
        }

        int u, v, w;
        while (P-- > 0) {
            st = new StringTokenizer(br.readLine());
            u = parseInt(st.nextToken());
            v = parseInt(st.nextToken());
            w = parseInt(st.nextToken());

            w = 2 * w + visitCost[u] + visitCost[v];
            pq.offer(new Edge(u, v, w));
        }

        int sum = kruskal(N) + visitCost[start];
        System.out.println(sum);
        br.close();
    }

    static int find(int u) {
        if (parent[u] < 0) return u;

        return parent[u] = find(parent[u]);
    }

    static boolean union(int u, int v) {
        int r1 = find(u);
        int r2 = find(v);

        if (r1 == r2) return false;

        if (parent[r1] < parent[r2]) {
            parent[r1] += parent[r2];
            parent[r2] = r1;
        } else {
            parent[r2] += parent[r1];
            parent[r1] = r2;
        }

        return true;
    }

    static int kruskal(int N) {
        Arrays.fill(parent, -1);
        int selected = 0, sum = 0;

        while (!pq.isEmpty() && selected < N - 1) {
            Edge e = pq.poll();

            if (!union(e.u, e.v)) continue;

            selected++;
            sum += e.w;
        }

        return sum;
    }

    static class Edge {
        int u, v, w;

        public Edge(int u, int v, int w) {
            this.u = u;
            this.v = v;
            this.w = w;
        }
    }
}

결과