백준 13023 - ABCDE

문제

https://www.acmicpc.net/problem/13023

풀이

DFS를 활용한 백트래킹을 통해 풀이할 수 있는 문제이다.

A-B-C-D-E 관계는 풀어서 생각해보면 한 정점에서 DFS를 탐색을 돌렸을 때 5개의 노드를
방문(깊이가 4)할 수 있는 경우로 해석할 수 있다. 다만, 주의해야할 점은 각 깊이에서
방문 처리를 체크-해제하며 모든 경로를 탐색해야 한다는 것이다.

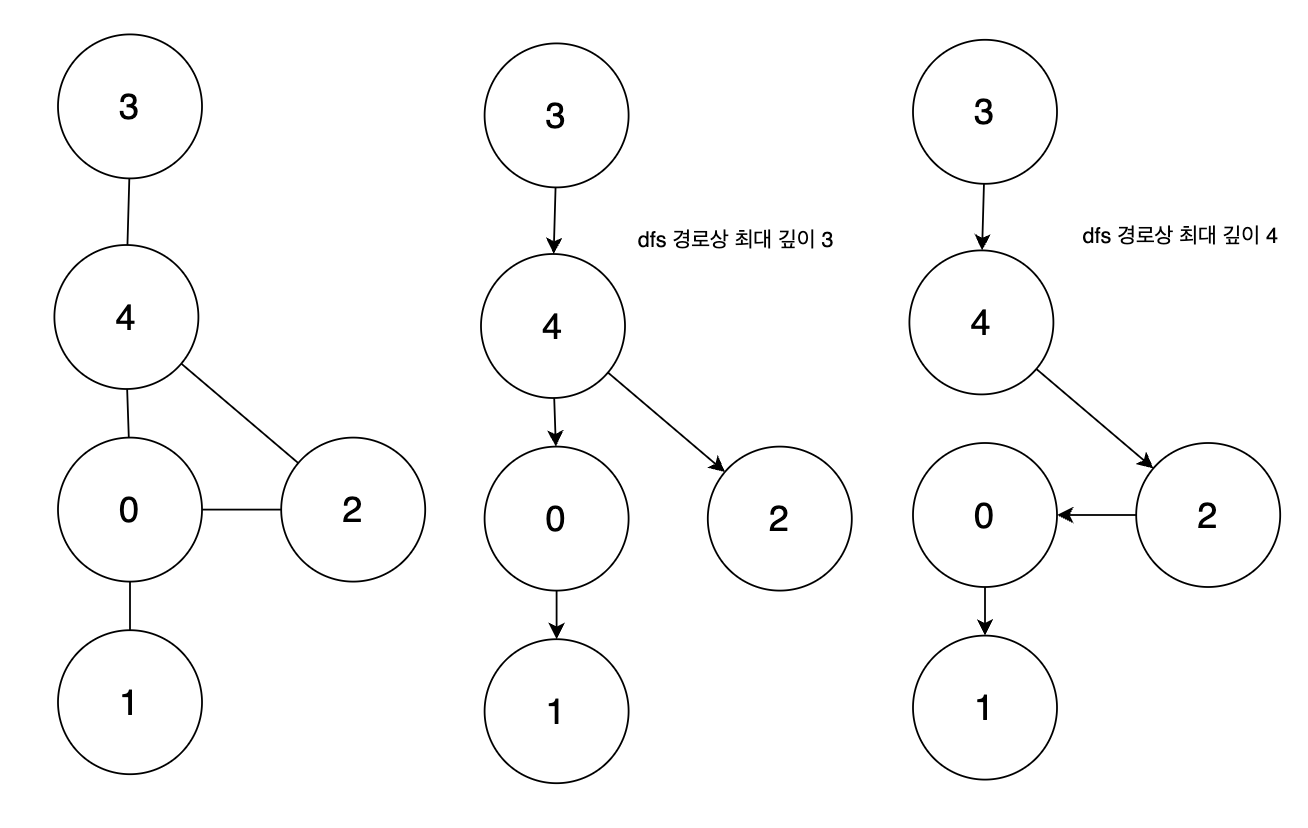
위 그림에서 주어진 그래프 상황을 통해 모든 경로를 탐색해야 하는 이유를 이해할 수 있다.
모든 경로를 고려하지 않으면 최대 깊이가 4가 되는 경로가 존재함에도 탐색하지 못하는
상황을 마주할 수 있다.

로직의 시간복잡도는 DFS가 최대 4의 깊이까지만 탐색을 진행하므로 각 정점에서 DFS를
호출하는 반복문에서 $O(N)$으로 수렴한다. 따라서 $N=2000$인 최악의 경우에도 무난히
제한 조건 2초를 통과한다.

코드

import java.io.*;
import java.util.*;

import static java.lang.Integer.parseInt;

public class Main {
    static boolean[] visited;
    static List<List<Integer>> graph = new ArrayList<>();
    static boolean answer = false;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = parseInt(st.nextToken());
        int m = parseInt(st.nextToken());

        visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }

        while (m-- > 0) {
            st = new StringTokenizer(br.readLine());
            int u = parseInt(st.nextToken());
            int v = parseInt(st.nextToken());

            graph.get(u).add(v);
            graph.get(v).add(u);
        }

        for (int i = 0; i < n; i++) {
            if (answer) break;
            dfs(i, 0);
        }

        System.out.println(answer ? 1 : 0);
        br.close();
    }

    static void dfs(int cur, int depth) {
        if (answer) return;
        if (depth == 4) {
            answer = true;
            return;
        }

        visited[cur] = true;
        for (int next : graph.get(cur)) {
            if (!visited[next]) {
                dfs(next, depth + 1);
            }
        }
        visited[cur] = false;
    }
}

결과