백준 14574 - 헤븐스 키친

문제

https://www.acmicpc.net/problem/14574

리뷰

크루스칼과 DFS를 통해 풀이할 수 있는 문제였다.

매일 둘씩 대결을 하므로 $N$명의 요리사가 존재할 때, $N-1$번의 대결이 펼쳐져야
하고 시청률의 합이 최댓값이 되어야 한다. 이 조건은 대결을 시청률을 비용으로 하는
간선(Edge)으로 표현하여 비용 기준 최대힙에 저장하였다가 크루스칼을 통해
$N-1$개의 간선을 채택하며 비용 합을 구하여 도출할 수 있었다.

까탈스러운 부분은 구성된 MST를 바탕으로 승자와 패자를 구분하여 대결 결과를
출력해야 한다는 점이었다. 결과적으로, 크루스칼을 구성하며 인접리스트의 형태로
MST를 표현한다면 DFS를 이용하여 답을 구할 수 있었다.

위 그림과 같은 MST가 존재한다고 가정하였을 때(편의상 비용은 생략)
승자와 패자를 어떻게 가를 것이냐를 생각해보면 가장 루트에 존재하는
(=먼저 DFS 탐색을 진행한) 노드를 승자를 보고, 리프에 해당하는(=상대적으로
나중에 DFS 탐색을 진행한) 노드를 패자로 보게 되면 승자와 패자를 쉽게
판별할 수 있음을 확인할 수 있다.

따라서 DFS 로직내에서 다음 노드로의 DFS 진행 후에 현재 노드 다음 노드 형태로
출력을 하게 되면

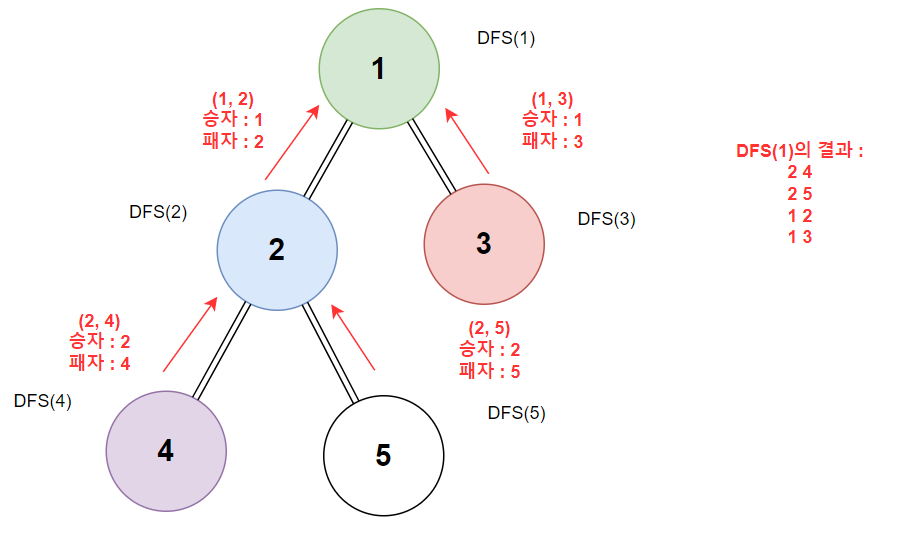
위와 같이 문제에서 요구하는 출력을 얻을 수 있다.

로직의 시간복잡도는 DFS가 $N+N-1=O(N)$, 크루스칼이
$N \times log(N(N-1))=O(NlogN)$ 형태를 띄므로 크루스칼의 $O(NlogN)$으로
수렴하게 되고, 이는 $N=1,000$인 최악의 경우에도 무난히 제한 조건 1초를
통과한다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

import static java.lang.Integer.*;

public class Main {
    static int[] parent;
    static boolean[] visited;
    static PriorityQueue<Edge> pq = new PriorityQueue<>((e1, e2) -> compare(e2.w, e1.w));
    static List<List<Integer>> graph;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = parseInt(br.readLine());
        parent = new int[N + 1];
        visited = new boolean[N + 1];

        int[] pValues = new int[N + 1];
        int[] cValues = new int[N + 1];

        StringTokenizer st;
        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            pValues[i] = parseInt(st.nextToken());
            cValues[i] = parseInt(st.nextToken());
        }

        int w;
        for (int u = 1; u < pValues.length - 1; u++)
            for (int v = u + 1; v < pValues.length; v++) {
                w = (cValues[u] + cValues[v]) / Math.abs(pValues[u] - pValues[v]);
                pq.offer(new Edge(u, v, w));
            }


        long sum = kruskal(N);
        System.out.println(sum);
        dfs(1);
        br.close();
    }

    static void dfs(int cur) {
        visited[cur] = true;


        for (Integer next : graph.get(cur)) {
            if (visited[next]) continue;

            dfs(next);
            System.out.println(cur + " " + next);
        }
    }

    static int find(int u) {
        if (parent[u] < 0) return u;

        return parent[u] = find(parent[u]);
    }

    static boolean union(int u, int v) {
        int r1 = find(u);
        int r2 = find(v);

        if (r1 == r2) return false;

        if (parent[r1] < parent[r2]) {
            parent[r1] += parent[r2];
            parent[r2] = r1;
        } else {
            parent[r2] += parent[r1];
            parent[r1] = r2;
        }

        return true;
    }

    static long kruskal(int N) {
        Arrays.fill(parent, -1);
        graph = new ArrayList<>();
        graph.add(null);
        for (int i = 0; i < N; i++) graph.add(new ArrayList<>());

        int selected = 0;
        long sum = 0;

        while (!pq.isEmpty() && selected < N - 1) {
            Edge e = pq.poll();

            if (!union(e.u, e.v)) continue;

            selected++;
            sum += e.w;
            graph.get(e.u).add(e.v);
            graph.get(e.v).add(e.u);
        }

        return sum;
    }

    static class Edge {
        int u, v, w;

        public Edge(int u, int v, int w) {
            this.u = u;
            this.v = v;
            this.w = w;
        }
    }
}

결과