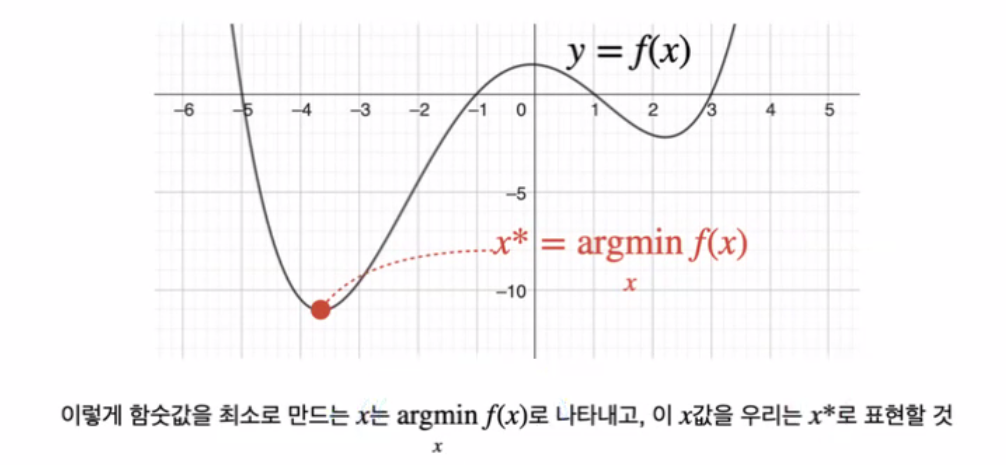
<수업 내용>
Gradient-based Learning
- stocastic gradient descent (SGD) by pytorch
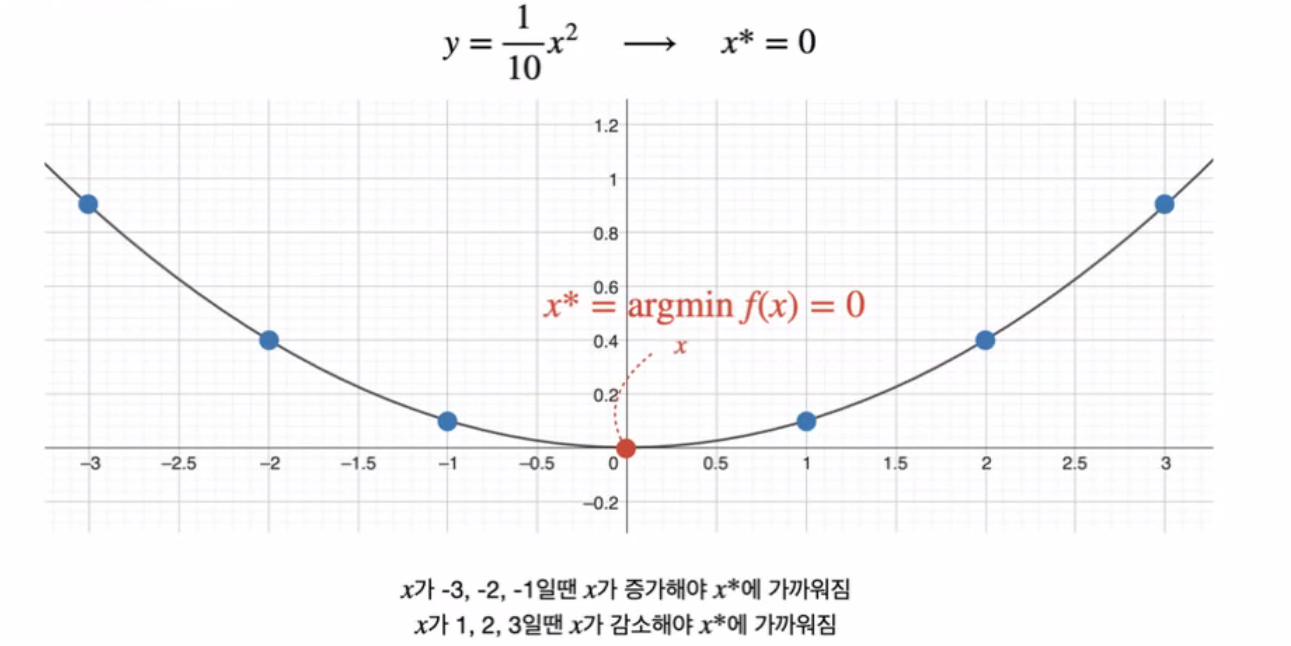


def df_dx(x):
return 1/5 * x
x = 3
iterations = 20
print(f'initial x : {x}')
for iter in range(iterations):
dy_dx = df_dx(x)
x = x-dy_dx
print(f'{iter + 1} - th x: {x :.4f}')import matplotlib.pyplot as plt
import numpy as np
def f(x):
return 1/5*(x**2)
def df_dx(x):
return 1/5 * x
x = 3
iterations = 20
x_track, y_track =[x], [f(x)]
for _ in range(iterations):
dy_dx = df_dx(x)
x = x-dy_dx
x_track.append(x)
y_track.append(f(x))
x_ = np.arange(-5,5,0.001)
y_ = f(x_)
fig, ax = plt.subplots(2,1,figsize=(20,5))
ax[0].plot(x_, y_)
ax[0].scatter(x_track, y_track, c=range(iterations +1), cmap ='rainbow')
ax[1].plot(x_track, marker='o')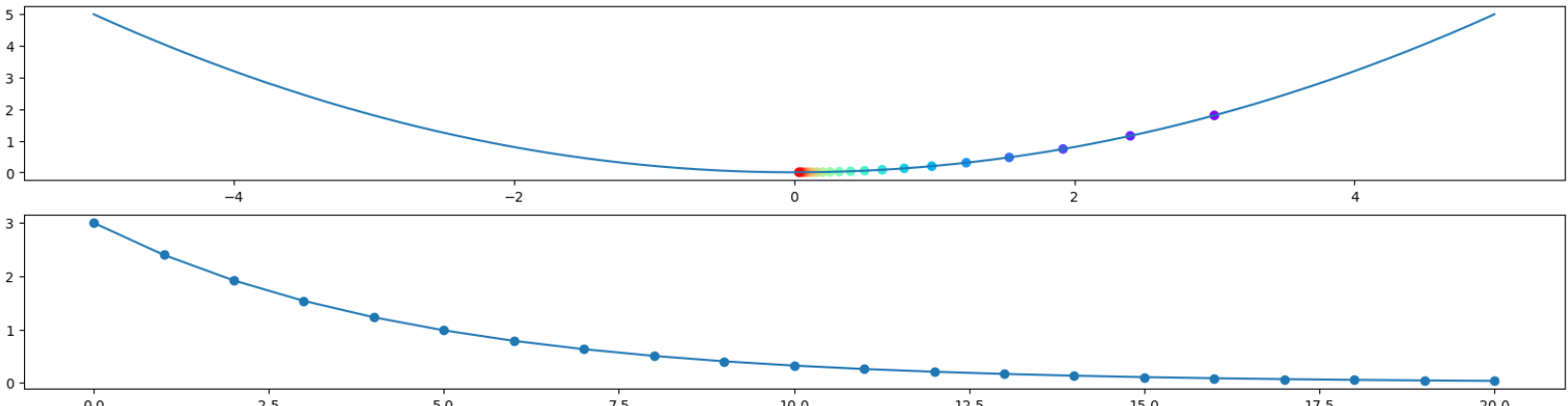
import matplotlib.pyplot as plt
import numpy as np
def f_1(x):
return 1/10*(x**2)
def df_dx_1(x):
return 1/5 * x
def f_2(x):
return 1/8*(x**2)
def df_dx_2(x):
return 1/4 * x
def f_3(x):
return 1/6*(x**2)
def df_dx_3(x):
return 1/3 * x
x1, x2, x3 = 3, 3, 3
iterations = 20
x_track1, y_track1 =[x1], [f_1(x1)]
x_track2, y_track2 =[x2], [f_2(x2)]
x_track3, y_track3 =[x3], [f_3(x3)]
for _ in range(iterations):
dy_dx1 = df_dx_1(x1)
x1 = x1-dy_dx1
x_track1.append(x1)
y_track1.append(f_1(x1))
for _ in range(iterations):
dy_dx2 = df_dx_2(x2)
x2 = x2-dy_dx2
x_track2.append(x2)
y_track2.append(f_2(x2))
for _ in range(iterations):
dy_dx3 = df_dx_3(x3)
x3 = x3-dy_dx3
x_track3.append(x3)
y_track3.append(f_3(x3))
x1 = np.arange(-5,5,0.001)
x2 = np.arange(-5,5,0.001)
x3 = np.arange(-5,5,0.001)
y_1 = f_1(x1)
y_2 = f_2(x2)
y_3 = f_3(x3)
fig, ax = plt.subplots(3,1,figsize=(10,8))
ax[0].plot(x1, y_1, c='skyblue')
ax[0].scatter(x_track1, y_track1, c=range(iterations +1), cmap ='rainbow')
ax[1].plot(x2, y_2, c='orange')
ax[1].scatter(x_track2, y_track2, c=range(iterations +1), cmap ='rainbow')
ax[2].plot(x3, y_3, c='green', alpha=0.5)
ax[2].scatter(x_track3, y_track3, c=range(iterations +1), cmap ='rainbow') 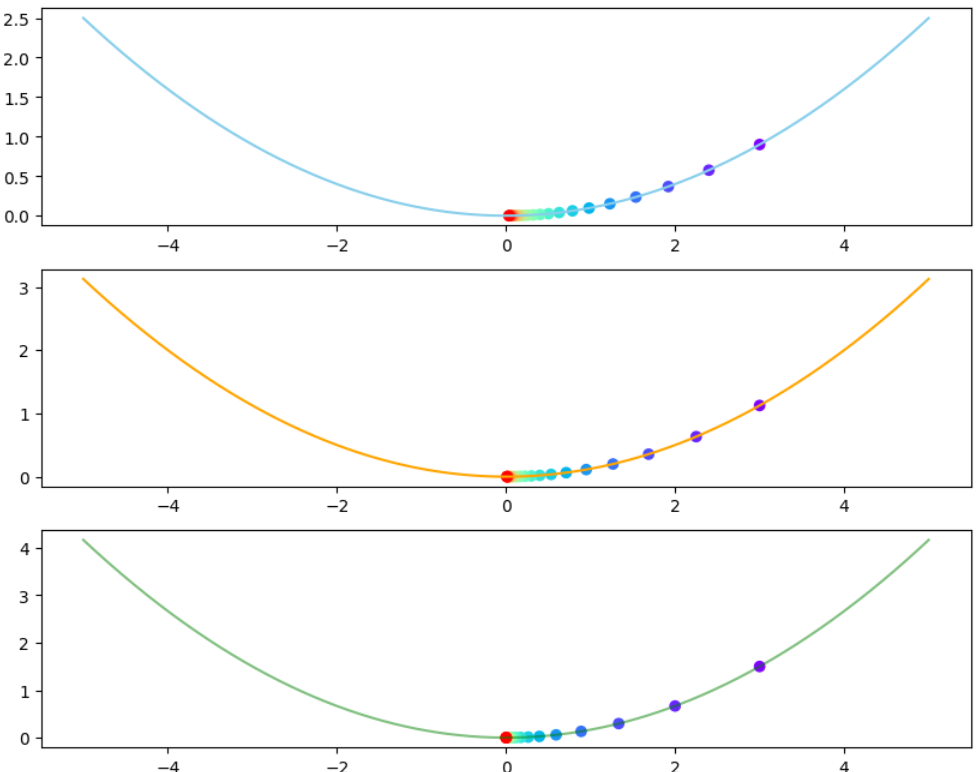
- 함수의 계수가 커질 수록 target x 에 다가가는 속도가 빨라진다
- 계수가 더 커지면, 지그재그로 다가가게 된다.
- 그러다가 gradient exploding problem이 발생
def f_1(x):
return 2*(x**2)
def df_dx_1(x):
return 4 * x
x1= 3
iterations = 20
x_track1, y_track1 =[x1], [f_1(x1)]
for _ in range(iterations):
dy_dx1 = df_dx_1(x1)
x1 = x1-dy_dx1
x_track1.append(x1)
y_track1.append(f_1(x1))
x1 = np.arange(-5,5,0.001)
y_1 = f_1(x1)
fig, ax = plt.subplots(2,1,figsize=(10,8))
ax[0].plot(x1, y_1, c='skyblue')
ax[0].scatter(x_track1, y_track1, c=range(iterations +1), cmap ='rainbow')
ax[1].plot(x_track1, marker='o')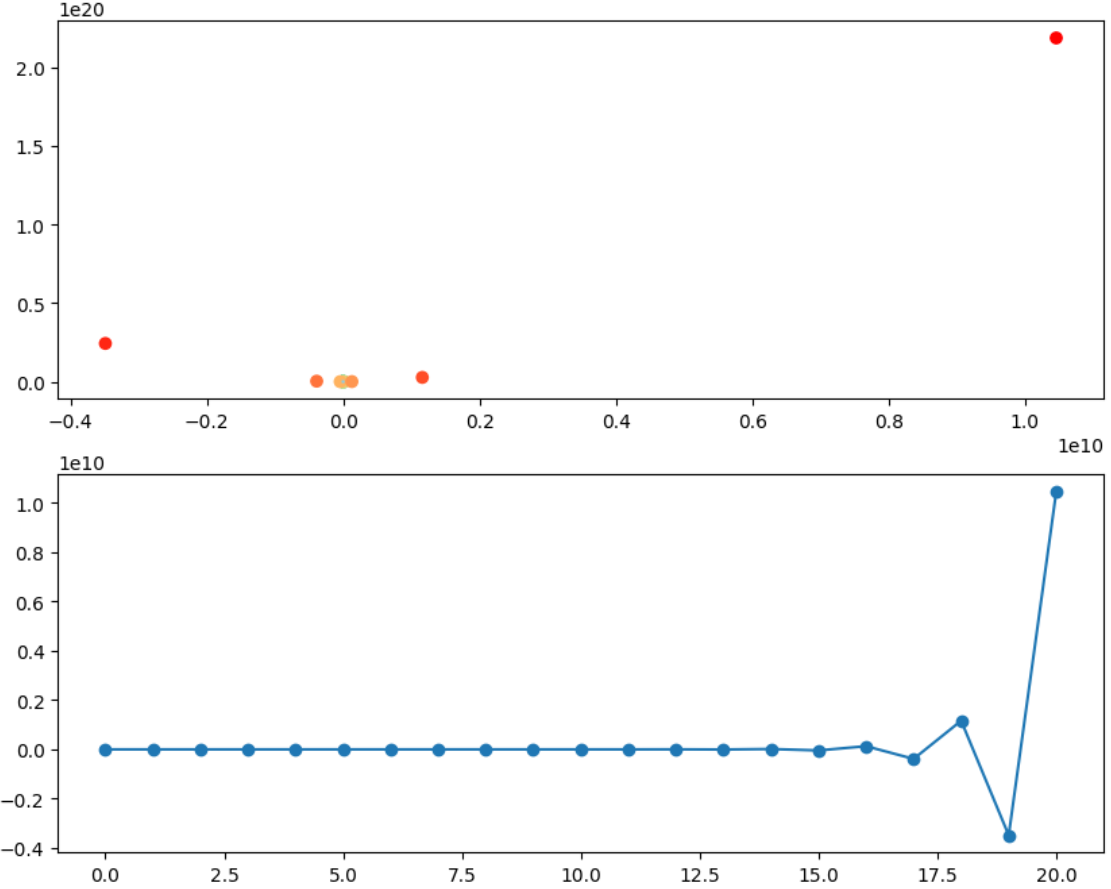

# learning rate = .1
def f_1(x):
return 2*(x**2)
def df_dx_1(x):
return 4 * x
x1= 3
iterations = 20
x_track1, y_track1 =[x1], [f_1(x1)]
lr = 0.1
for _ in range(iterations):
dy_dx1 = df_dx_1(x1)
x1 = x1-lr*(dy_dx1)
x_track1.append(x1)
y_track1.append(f_1(x1))
print(x_track1)
x1 = np.arange(-5,5,0.001)
y_1 = f_1(x1)
fig, ax = plt.subplots(2,1,figsize=(10,8))
ax[0].plot(x1, y_1, c='skyblue')
ax[0].scatter(x_track1, y_track1, c=range(iterations +1), cmap ='rainbow')
ax[1].plot(x_track1, marker='o')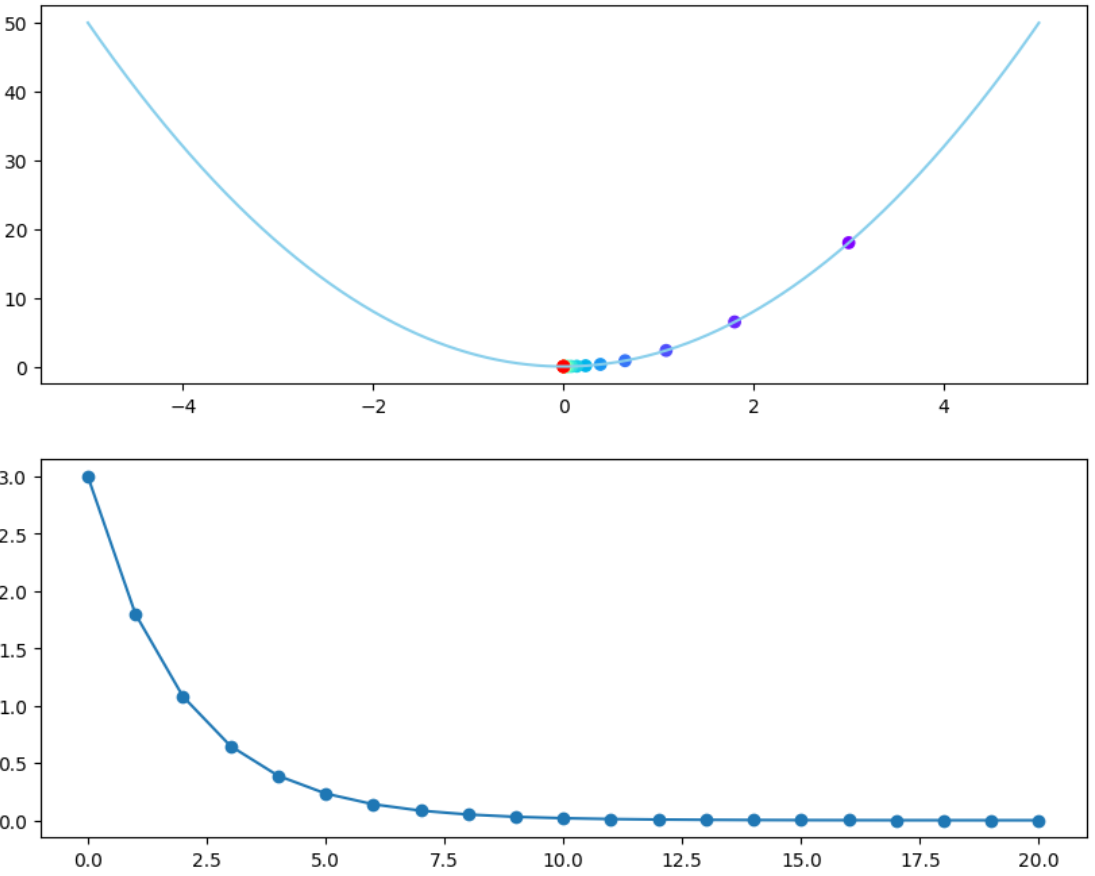

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
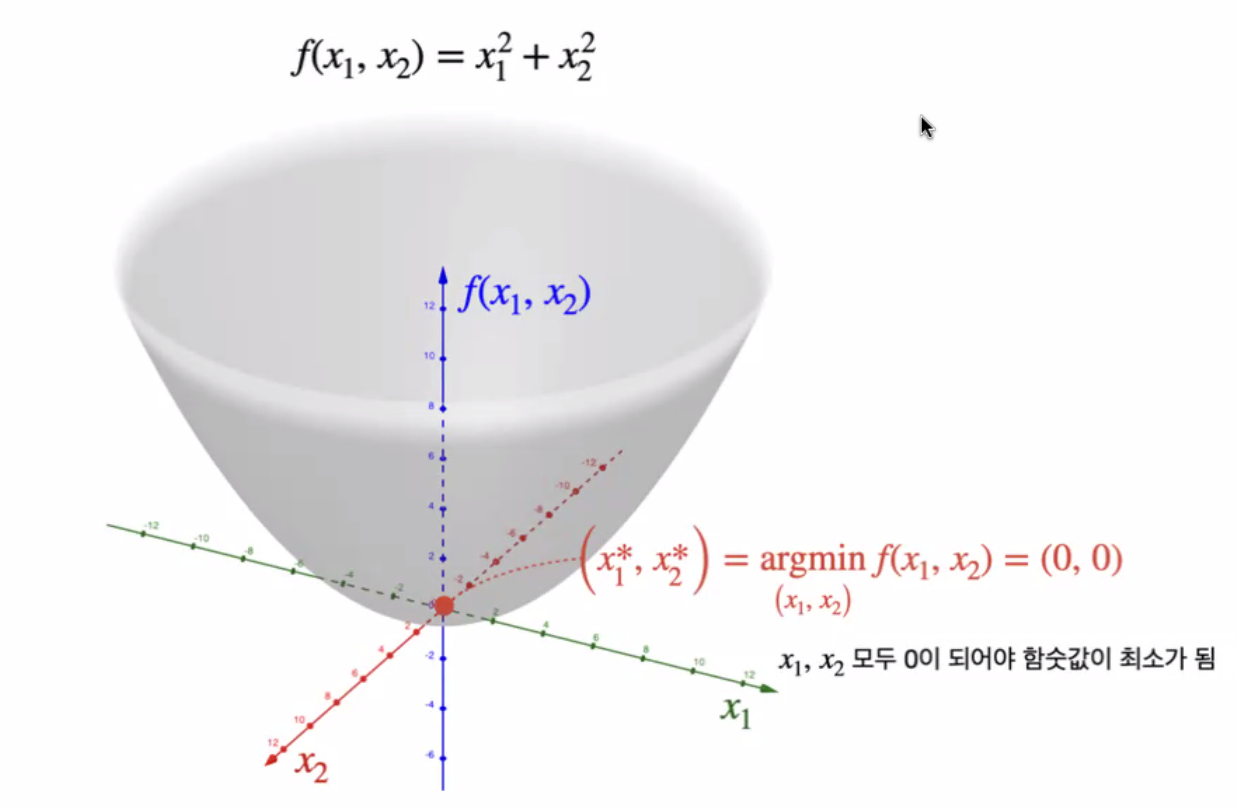
def f(x1, x2):
return x1**2 + x2**2
def dy_dx1(x1):
return 2*x1
def dy_dx2(x2):
return 2*x2
x1 = 3
x2 = 3
iterations = 20
x_track1, x_track2, y_track = [x1], [x2], [f(x1, x2)]
for _ in range(iterations):
df_dx1 = dy_dx1(x1)
x1 = x1 - 0.1*df_dx1
x_track1.append(x1)
df_dx2 = dy_dx2(x2)
x2 = x2 - 0.1*df_dx2
x_track2.append(x2)
y_track.append(f(x1, x2))
x1 = np.arange(-5, 5, 0.001)
x2 = np.arange(-5, 5, 0.001)
x1_m, x2_m = np.meshgrid(x1, x2)
y = f(x1_m, x2_m)
fig = plt.figure(figsize=(10, 20))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x1_m, x2_m, y, alpha=0.3)
ax.scatter(x_track1, x_track2, y_track, c=range(iterations + 1), cmap='rainbow', s=30, edgecolor='k')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('f(x1, x2)')
plt.show()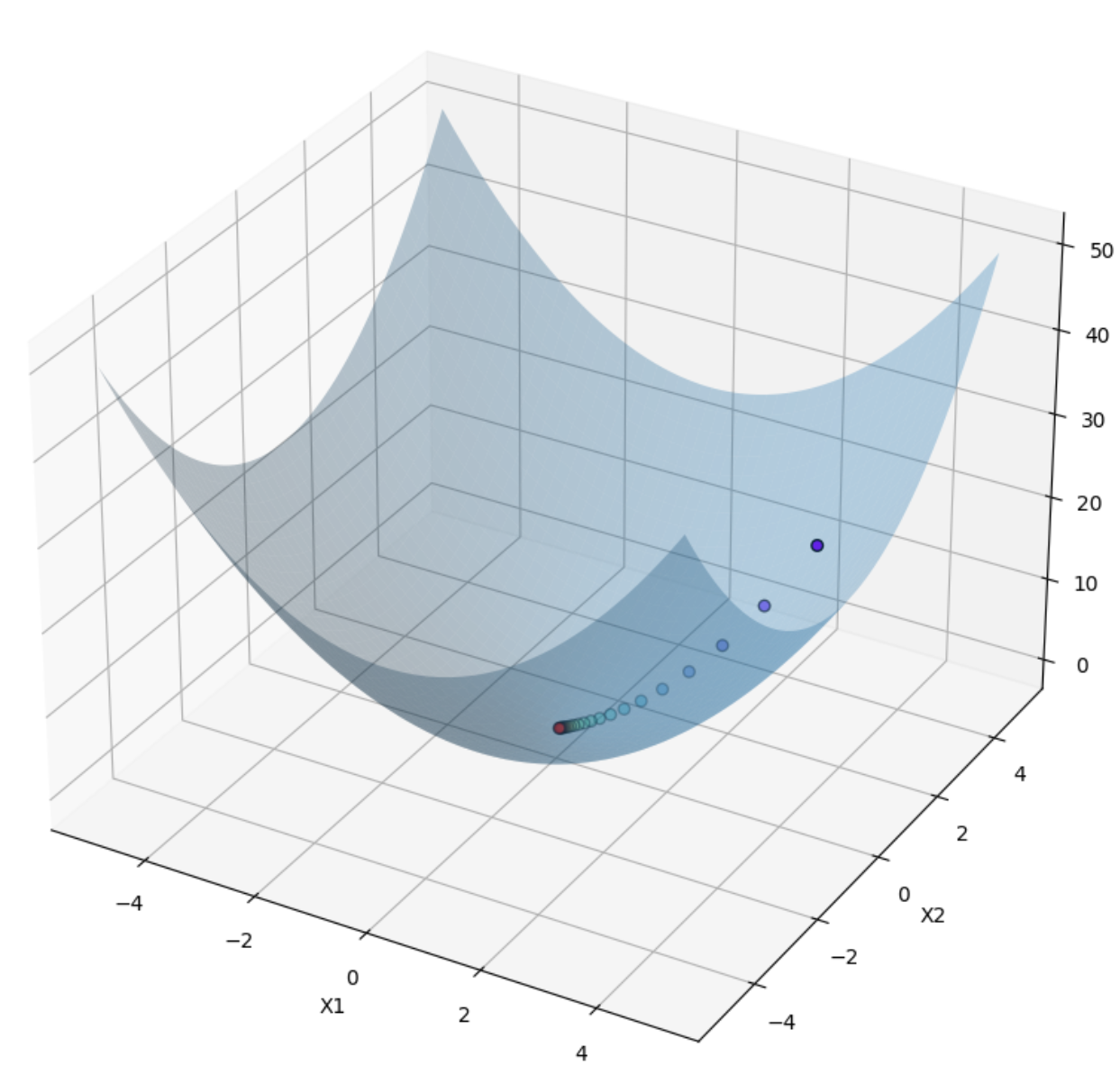
import matplotlib.pyplot as plt
import numpy as np
def f(x1, x2):
return x1**2 + x2**2
def dy_dx1(x1):
return 2*x1
def dy_dx2(x2):
return 2*x2
x1 = 3
x2 = 3
iterations = 20
x_track1, x_track2, y_track = [x1], [x2], [f(x1, x2)]
lr=0.1
for _ in range(iterations):
df_dx1 = dy_dx1(x1)
x1 = x1 -lr*df_dx1
x_track1.append(x1)
df_dx2 = dy_dx2(x2)
x2 = x2 - lr*df_dx2
x_track2.append(x2)
y_track.append(f(x1, x2))
x1 = np.arange(-5, 5, 0.01)
x2 = np.arange(-5, 5, 0.01)
x1 = np.linspace(-5, 5, 100)
x2 = np.linspace(-5, 5, 100)
x1_m, x2_m = np.meshgrid(x1, x2)
y =np.log(f(x1_m, x2_m))
fig, ax = plt.subplots(figsize=(10, 10))
ax.contour(x1_m,x2_m,y,levels=100,cmap='Blues alpha=0.6)
ax.scatter(x_track1,x_track2, c=range(iterations + 1), cmap='rainbow', s=30, edgecolor='k')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.tick_params(labelsize=15)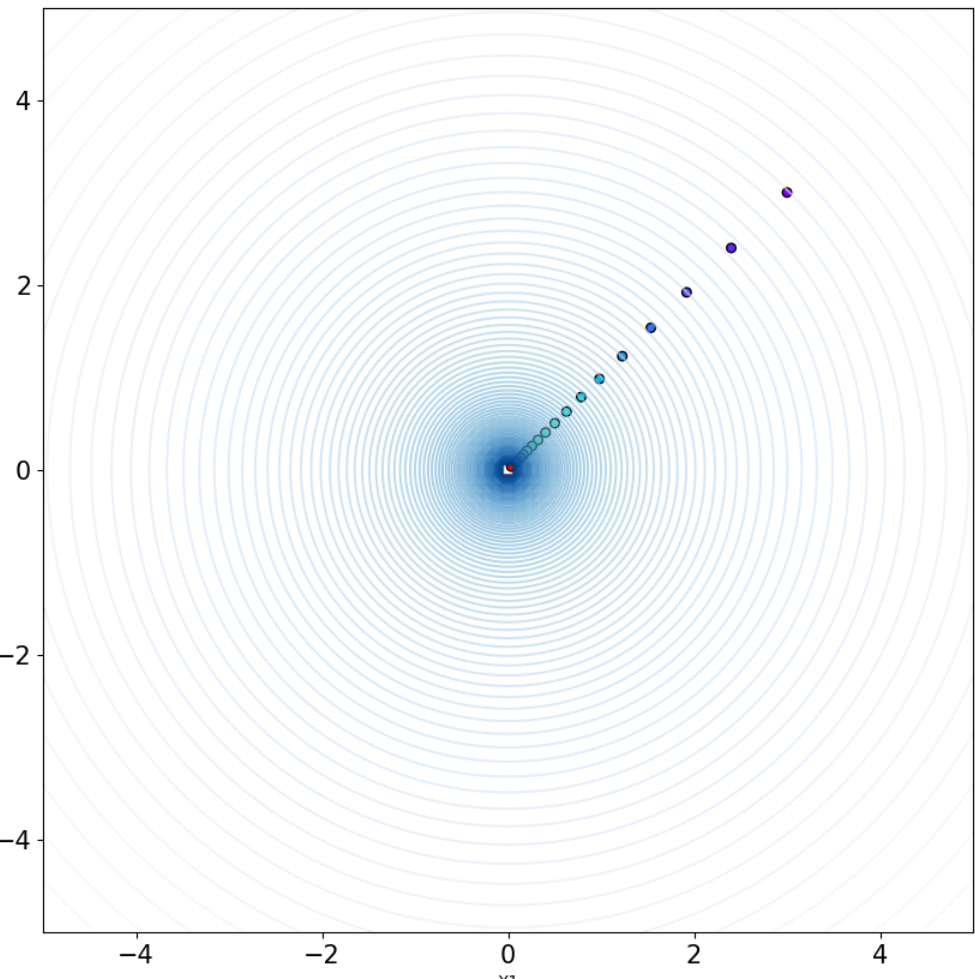
import matplotlib.pyplot as plt
import numpy as np
def f(x1, x2):
return 2*x1**2 + 7*x2**2
def dy_dx1(x1):
return 4*x1
def dy_dx2(x2):
return 14*x2
x1 = 3
x2 = 3
iterations = 20
x_track1, x_track2, y_track = [x1], [x2], [f(x1, x2)]
lr=0.03
for _ in range(iterations):
df_dx1 = dy_dx1(x1)
x1 = x1 -lr*df_dx1
x_track1.append(x1)
df_dx2 = dy_dx2(x2)
x2 = x2 - lr*df_dx2
x_track2.append(x2)
y_track.append(f(x1, x2))
x1 = np.arange(-5, 5, 0.01)
x2 = np.arange(-5, 5, 0.01)
x1 = np.linspace(-5, 5, 100)
x2 = np.linspace(-5, 5, 100)
x1_m, x2_m = np.meshgrid(x1, x2)
y =np.log(f(x1_m, x2_m))
fig, ax = plt.subplots(figsize=(10, 10))
ax.contour(x1_m,x2_m,y,levels=100,cmap='Blues_r', alpha=0.6)
ax.plot(x_track1,x_track2, marker="o", c='Orange', alpha=0.6)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.tick_params(labelsize=15)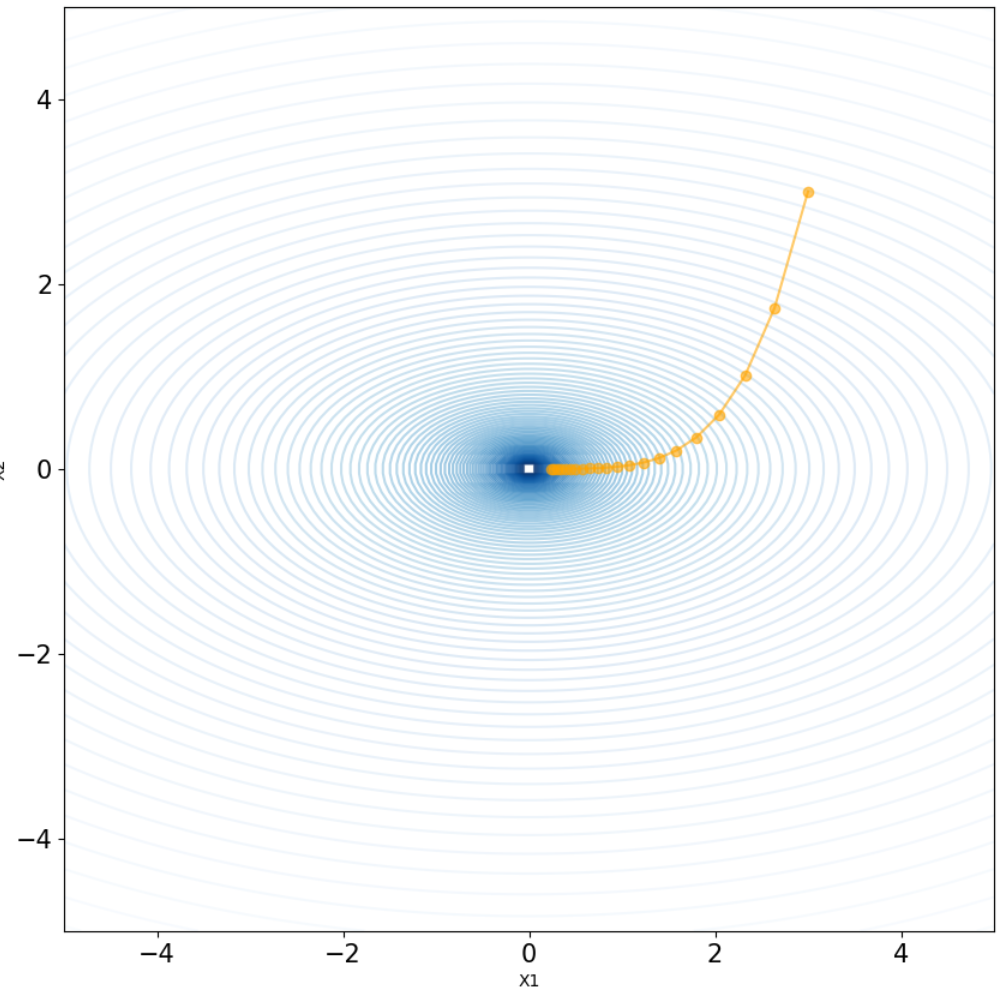
- 베이즈 정리가 하이퍼 파라미터 최적화에 적용된다.
Backpropagation

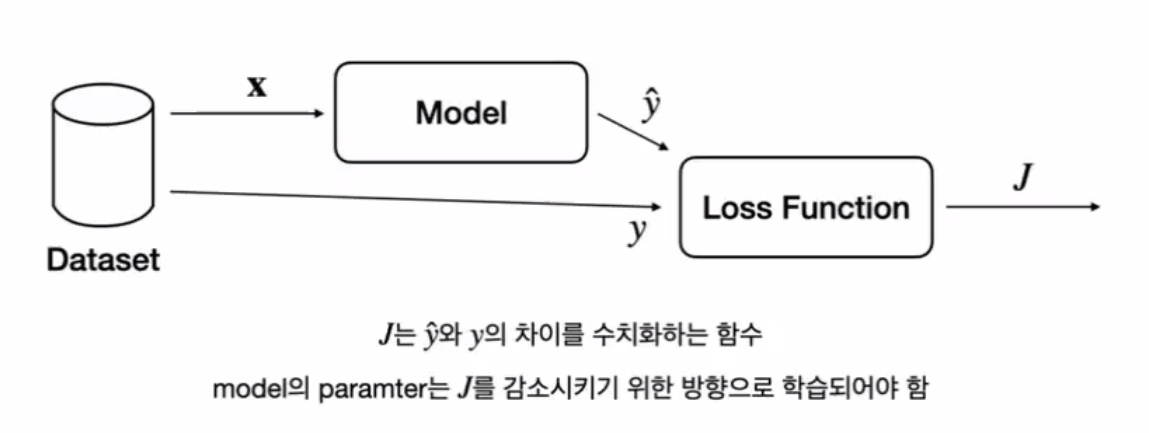
- lossfuction은 weight와 bias의 함수이다
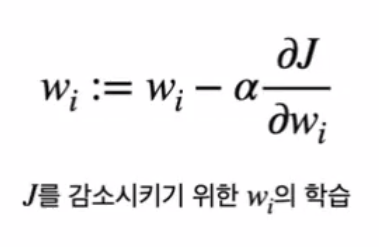
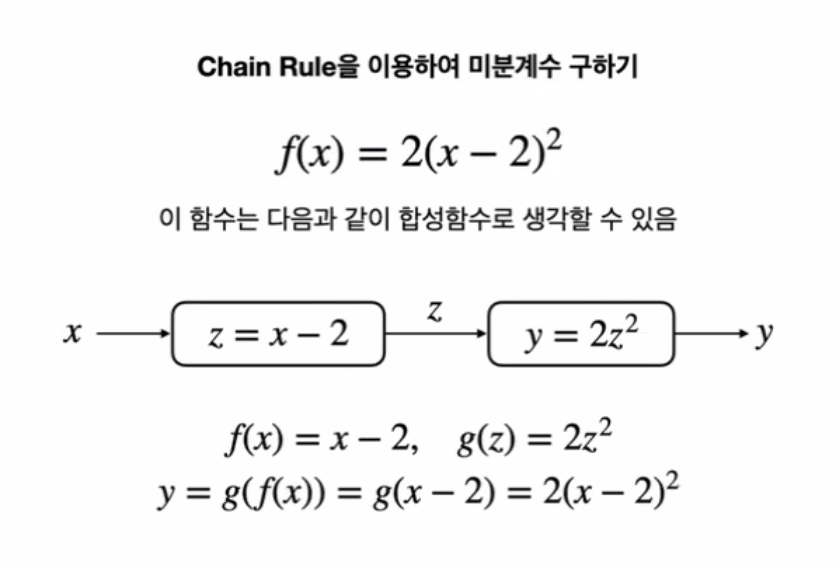
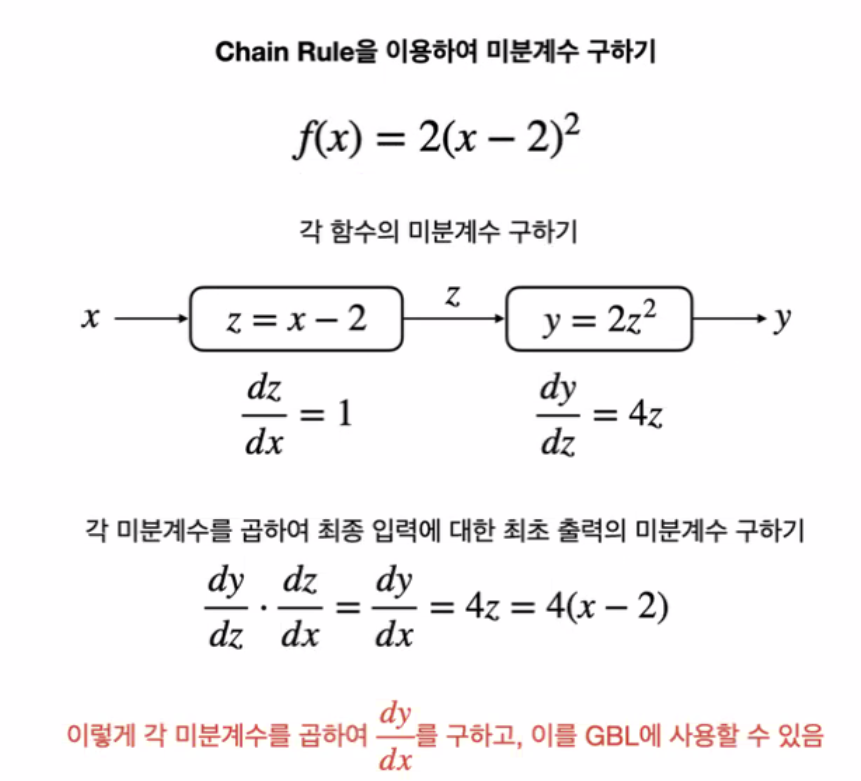

class Functiona1:
def forward(self, x):
z = x-2
def backward(self, dy_dz):
dy_dx = 1 * dy_dz
return dy_dx
class Function2:
def forward(self, z):
self.z = z
y = 2*z**2
def backward(self):
dy_dz = 4*self.z
return dy_dz
class Function:
def __init__(self):
self.func1 = Function1()
self.func2 = Function2()
def forward(self, x):
self.z = self.func1.forward(x)
k =self.func2.forward(self.z)
return k
def backward(self):
dy_dz = self.func2.backward()
l = self.func1.backward(dy_dz)
return l
x = 5
func = Function()
print(func.forward(5))
print(func.backward())
-------------------------
18
12 