[청년취업사관학교 새싹]핀테커스 수업 12주차(11/6)

<수업 내용>

Deeplearning

• 인공뉴런으로 학습한다
• framework : 일정한 형식이 짜여져 있어 그에 맞춰주어야 한다(라이브러리 사용과 다른점) , pytorch 등

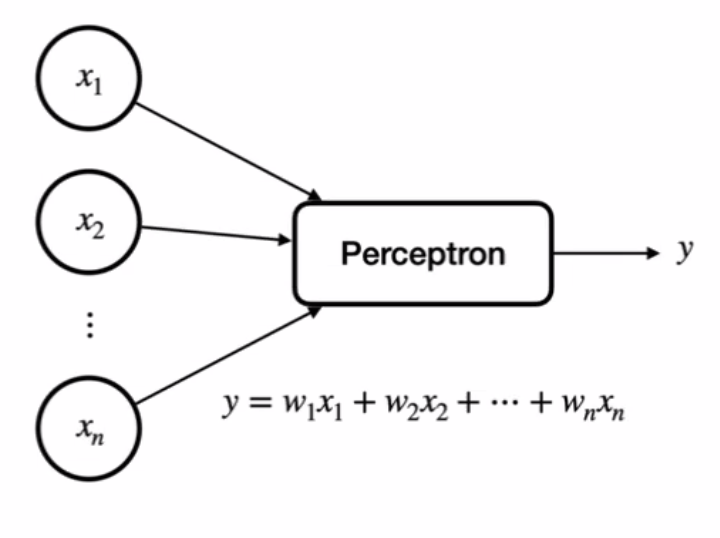
Perceptron

• 인공뉴런의 가장 기초적인 구조
• 뇌를 수학적으로 모방
• 입력에 각각 weight를 곱하고 bias(임계값)를 더한 연산을 하는 함수
• $(입력값)*(weight)$의 연산 결과가 임계값을 넘으면 1을 출력, 임계값을 넘지 않으면 0을 출력
• weight : 중요도, bias : 뉴런의 활성도 > 적절한 parameter 를 찾아내는 것이 목표

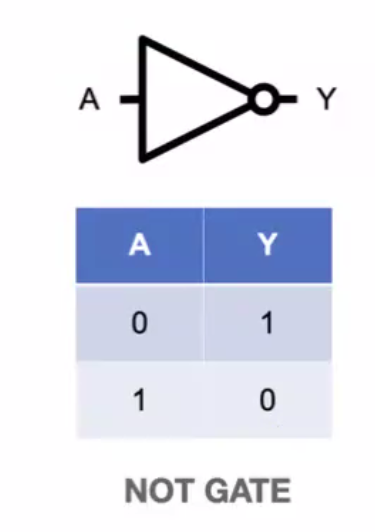
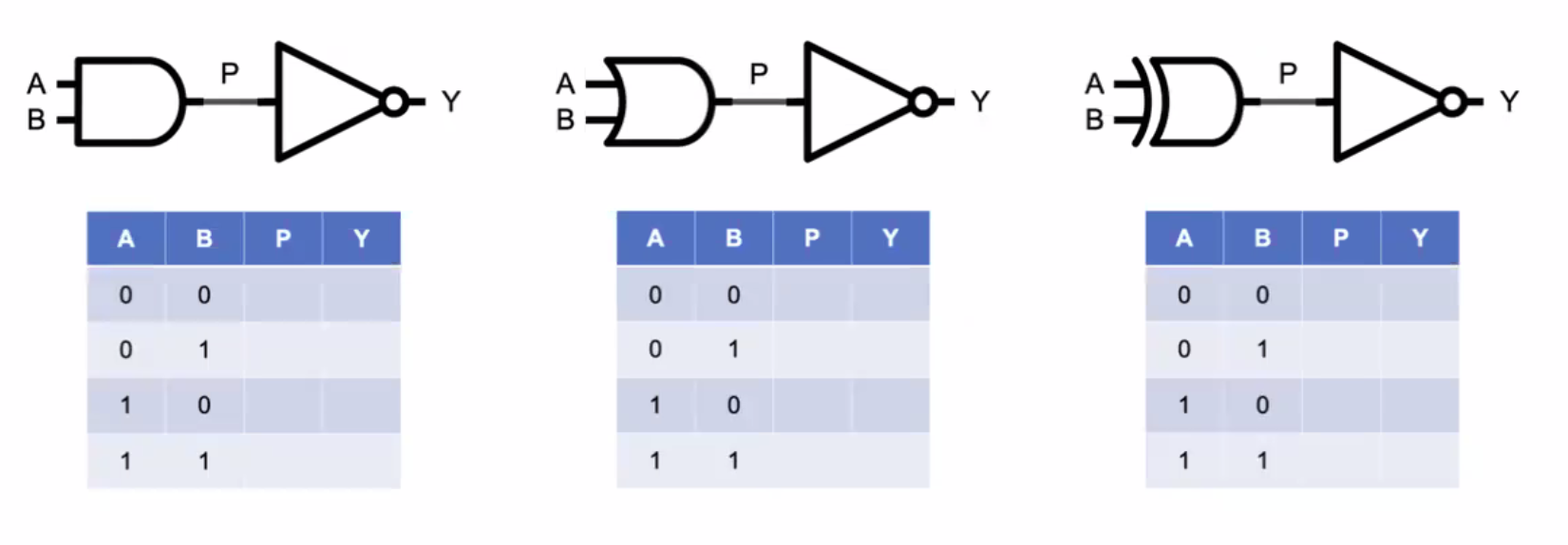
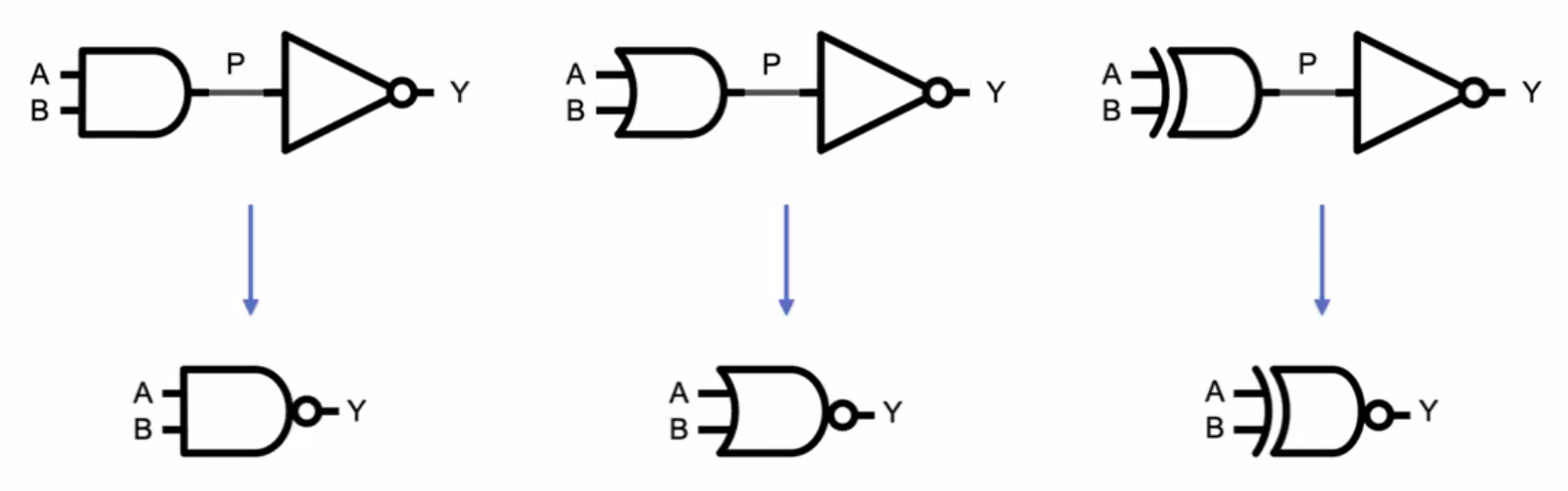
LogicGate

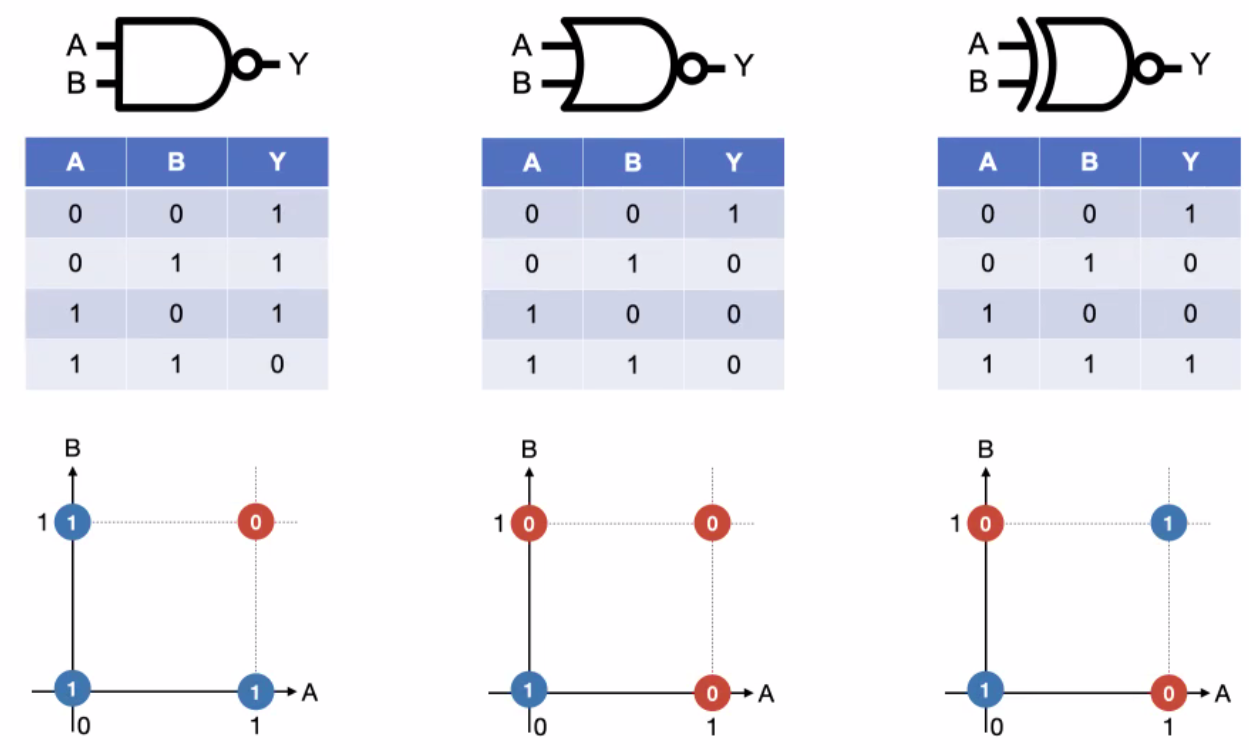
• not gate : 입력값의 반대 값을 출력
  
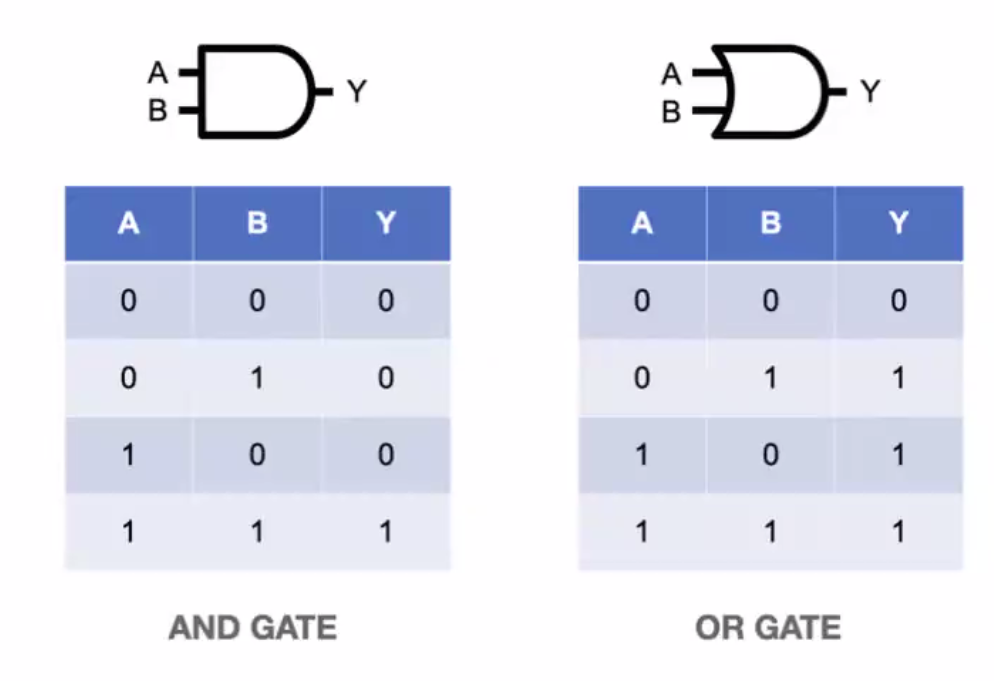
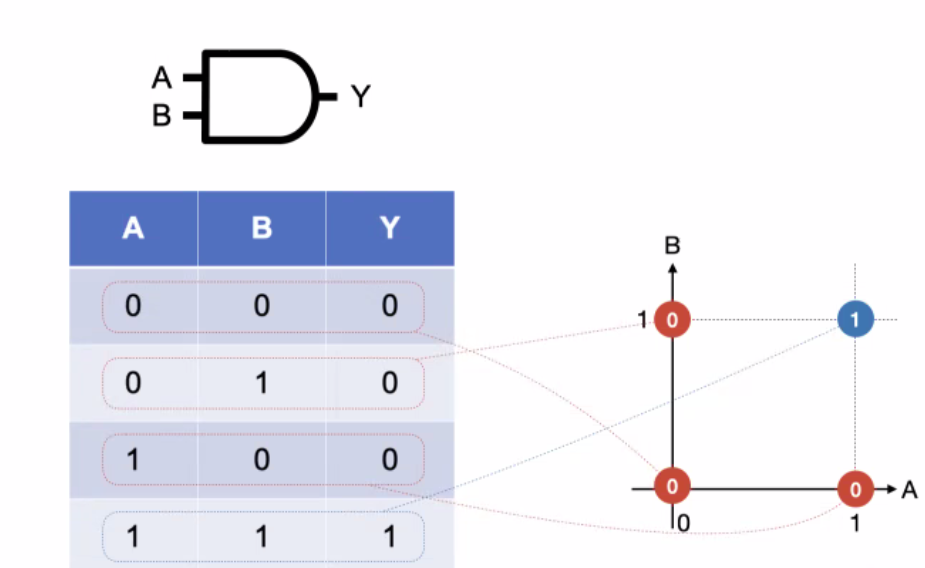
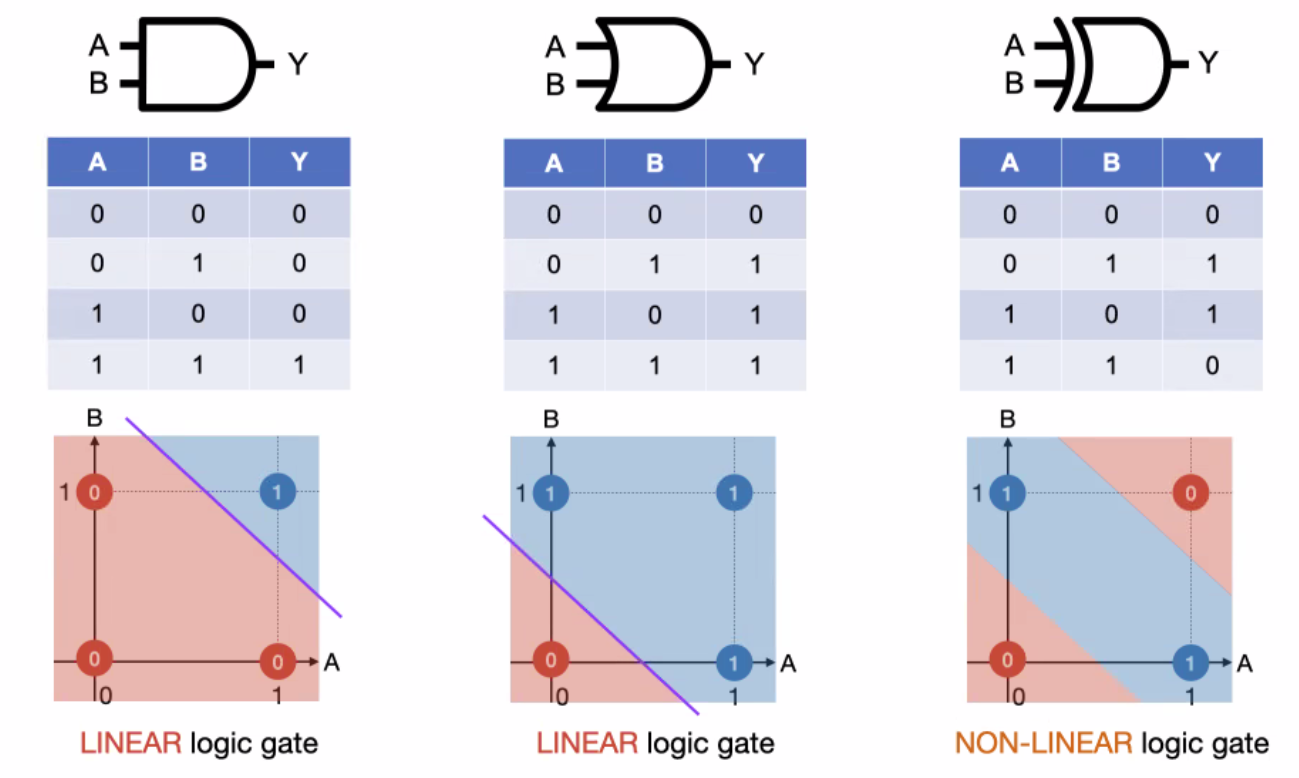
• and gate : 모두 1일 경우에만 1을 출력
• or gate : 둘 중 하나라고 1일 경우 1을 출력
  
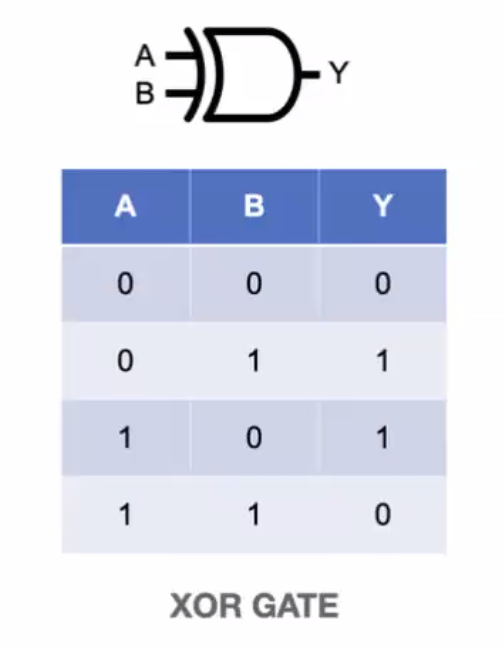
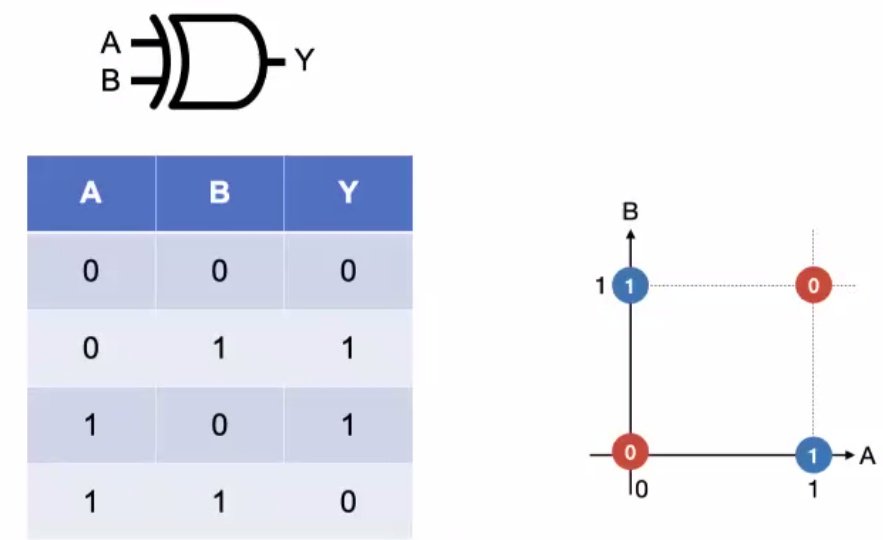
• xor gate: 1이 하나(홀수)일 때만 1을 출력, 나머지는 0을 출력
  
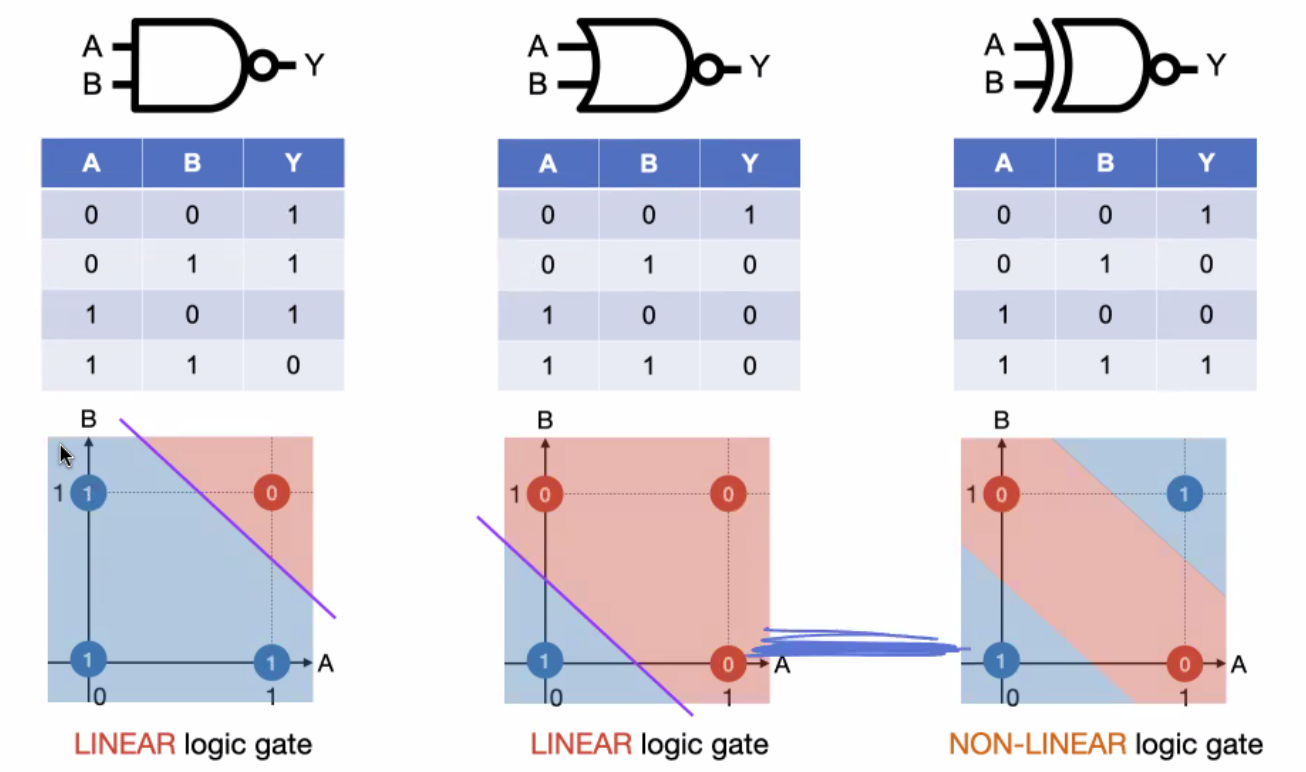
• NAND,NOR,XNOR gate
  
  
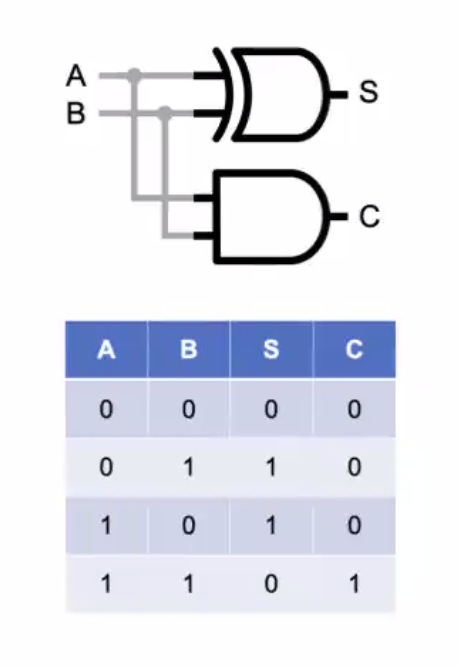
• Half Adder(덧셈기) : $2^0$자리의 덧셈기
  
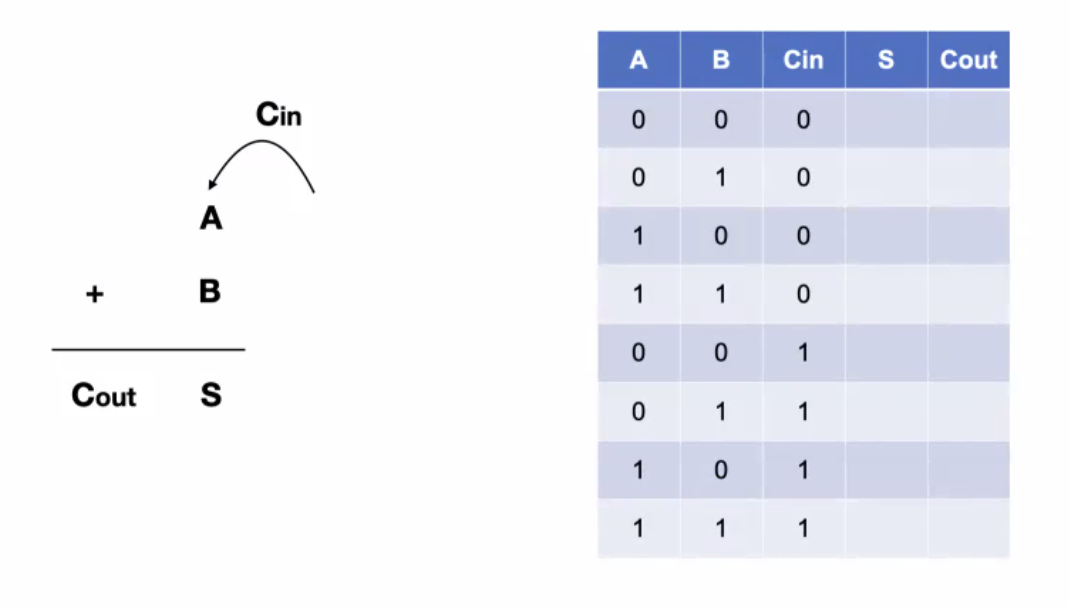
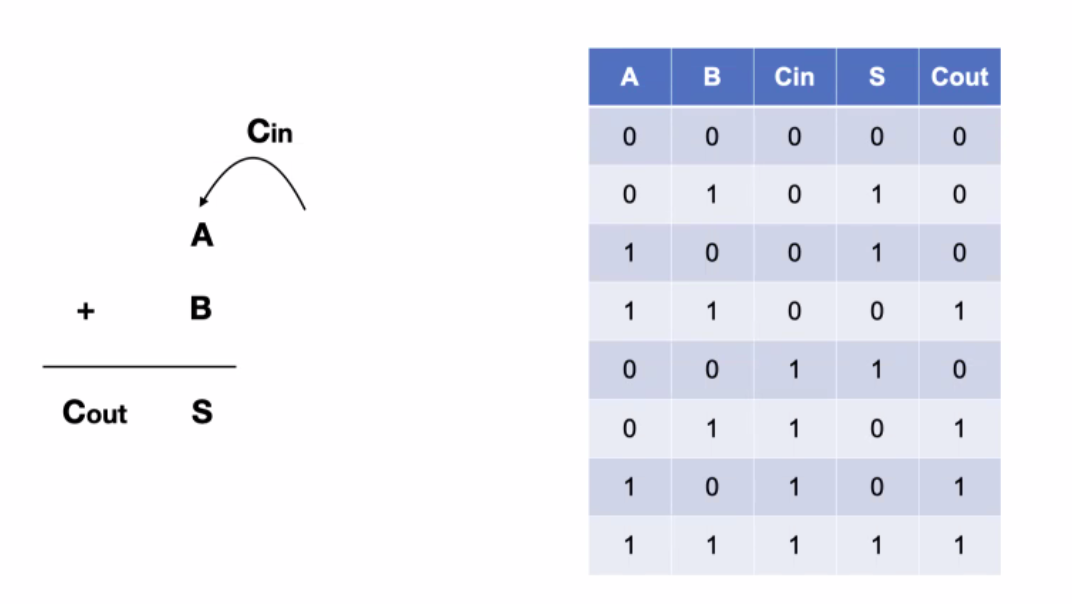
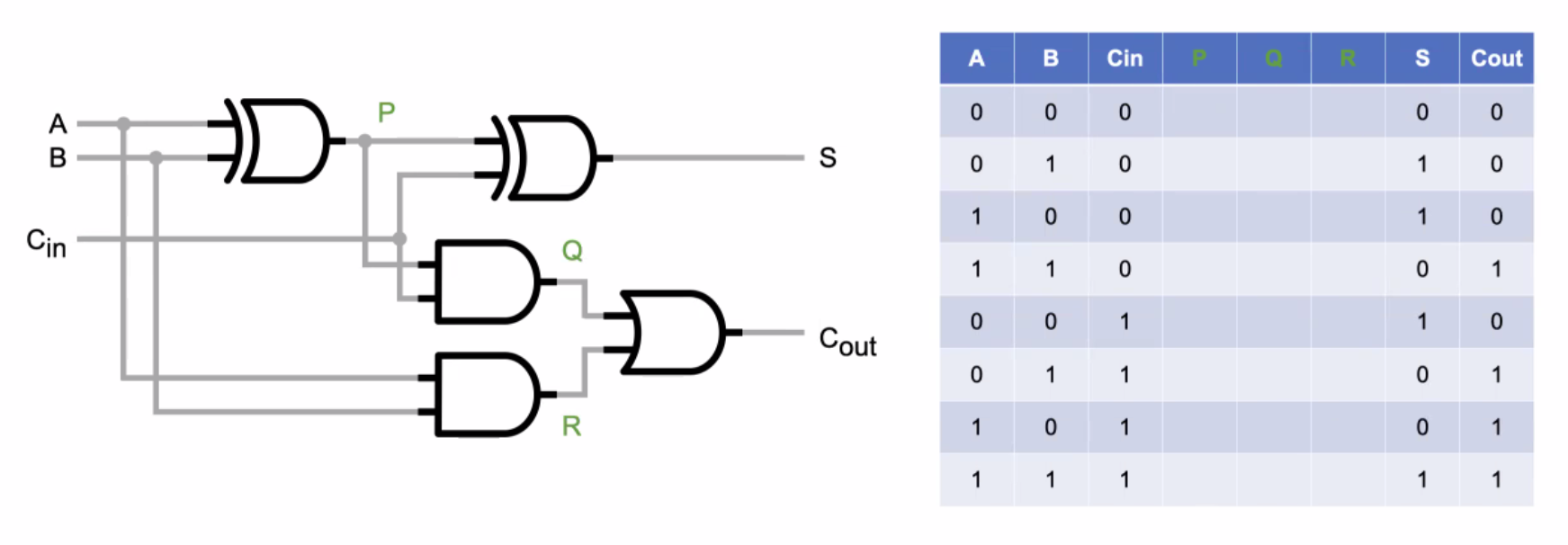
• Full Adder :carry over 되는 값을 고려하는 덧셈기
  
  

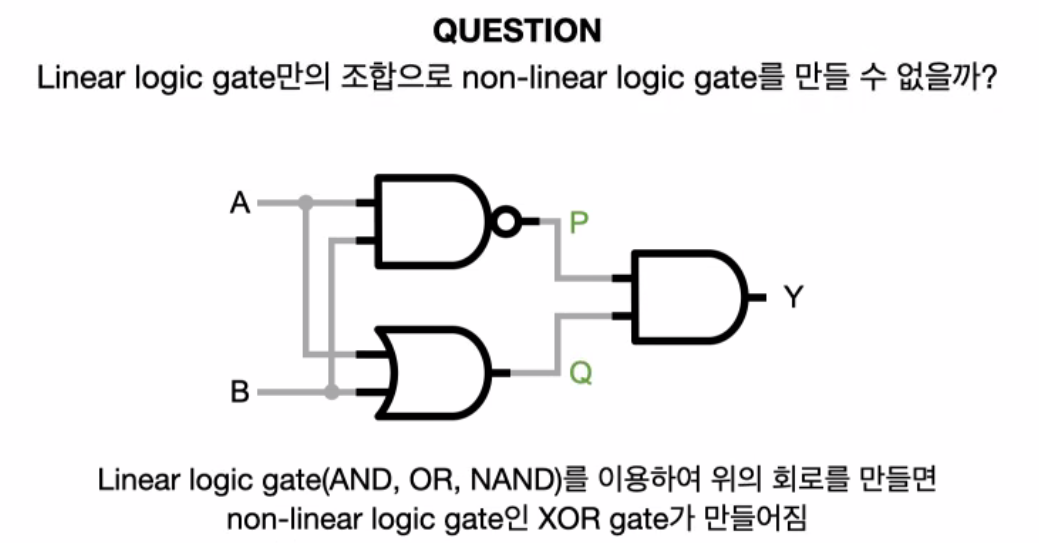
• AND가 만드는 0,1의 구역은 직선 하나로 나눌 수 있다. = dicision boundary가 linear 하다.(Linear logic gate)
  
  
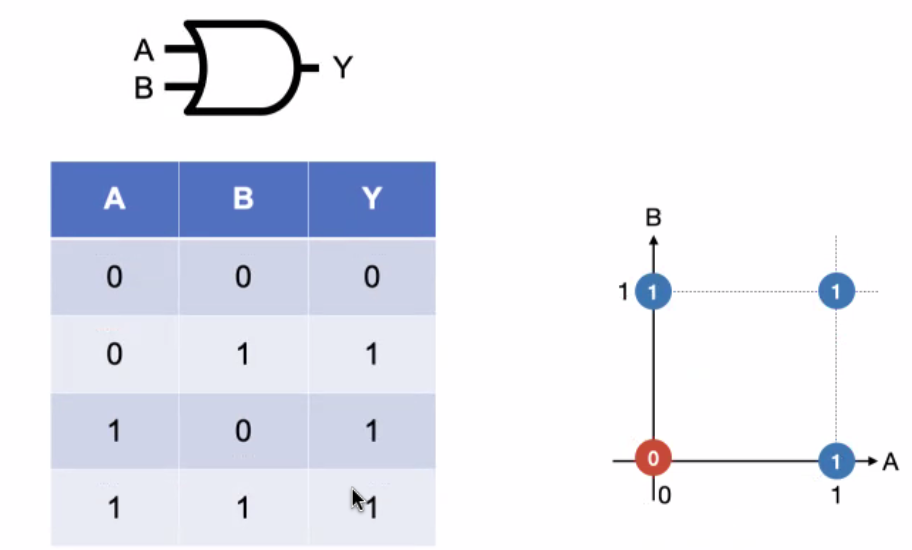
• XOR가 만드는 0,1의 구역은 직선 하나로 나눌 수 없다. = dicision boundary 가 non-linear 하다.(Non-Linear logic gate)
  
  

• single layer perceptron : and, or , nand, nor
• multi layer perceptron : xor, xnor

def AND(x_1, x_2, wieght=1, bias=1.5):
  if x_1 + x_2 - bias > 0:
    return 1
  else: return 0
  
def OR(x_1, x_2, wieght=1, bias=0.5):
  if x_1 + x_2 - bias > 0:
    return 1
  else: return 0

def NAND(x_1, x_2, wieght=1, bias=1.5):
  if x_1 + x_2 - bias > 0:
    return 0
  else: return 1
  
def NOR(x_1, x_2, wieght=1, bias=0.5):
  if x_1 + x_2 - bias > 0:
    return 0
  else: return 1


def XOR (x_1, x_2, wieght=1, bias_1=1.5, bias_2=0.5):
  return AND(OR(x_1, x_2, wieght, bias_2), NAND(x_1, x_2, wieght, bias_1), wieght, bias_1)
  
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))

>>
0
1
1
0

def XNOR (x_1, x_2, wieght=1, bias_1=1.5, bias_2=0.5):
  return int(not(XOR(x_1, x_2, wieght, bias_1, bias_2)))  
  
print(XNOR(0,0))
print(XNOR(0,1))
print(XNOR(1,0))
print(XNOR(1,1))

>>
1
0
0
1

def half_adder(x_1, x_2, wieght=1, bias_1=1.5, bias_2=0.5):
  s=XOR (x_1, x_2, wieght, bias_1, bias_2)
  c=AND(x_1, x_2, wieght, bias_1)
  return x_1,x_2,s,c

print(half_adder(0,0))
print(half_adder(0,1))
print(half_adder(1,0))
print(half_adder(1,1))

>>
(0, 0, 0, 0)
(0, 1, 1, 0)
(1, 0, 1, 0)
(1, 1, 0, 1)

def full_adder(x_1, x_2, Cin, wieght=1, bias_1=1.5, bias_2=0.5):
  P=XOR (x_1, x_2, wieght, bias_1, bias_2)
  Q=AND(P, Cin, wieght, bias_1)
  R=AND(x_1, x_2, wieght, bias_1)
  S=XOR (P, Cin, wieght, bias_1, bias_2)
  Cout=OR(Q, R, wieght, bias_2)
  return x_1, x_2, P, Q, R, S, Cout
  
print(full_adder(0,0,0))
print(full_adder(0,1,0))
print(full_adder(1,0,0))
print(full_adder(1,1,0))
print(full_adder(0,0,1))
print(full_adder(0,1,1))
print(full_adder(1,0,1))
print(full_adder(1,1,1))

>>
(0, 0, 0, 0, 0, 0, 0)
(0, 1, 1, 0, 0, 1, 0)
(1, 0, 1, 0, 0, 1, 0)
(1, 1, 0, 0, 1, 0, 1)
(0, 0, 0, 0, 0, 1, 0)
(0, 1, 1, 1, 0, 0, 1)
(1, 0, 1, 1, 0, 0, 1)
(1, 1, 0, 0, 1, 1, 1)

import numpy as np

size=8
a=np.round((np.random.randint(0,2,size))).tolist()
b=np.round((np.random.randint(0,2,size))).tolist()
print(a, b)

## 이진수 더하기 함수
def adder(a,b, weight=1, bias_1=1.5, bias_2=0.5):
  a.reverse()
  b.reverse()
  
  first=half_adder(a[0], b[0], weight, bias_1, bias_2)
  Cin=first[3]
  answer=[first[2]]
  for i in range(1, len(a)):
    next=full_adder(a[i], b[i], Cin, weight, bias_1, bias_2)
    answer.append(next[6])
    Cin=next[7]
    if i == len(a)-1:
      answer.append(next[7])
  answer.reverse()
  return answer
>>
[0, 0, 1, 0, 0, 1, 1, 0] [0, 1, 1, 1, 0, 0, 1, 0]

adder(a, b, weight=1, bias_1=1.5, bias_2=0.5)
>>
[1, 0, 0, 1, 1, 0, 0, 0]