[청년취업사관학교 새싹]핀테커스 수업 12주차(11/9)

<수업 내용>

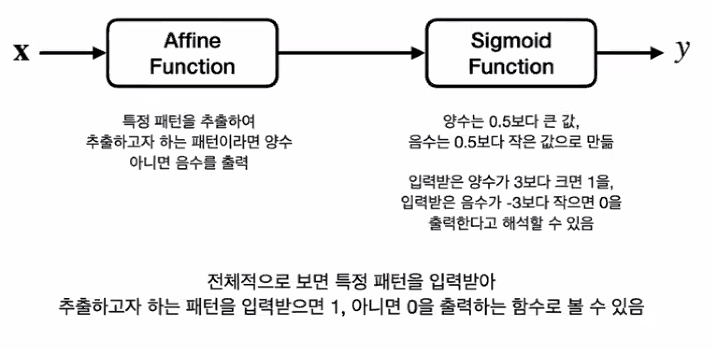
Artificial Neurons

• 어떠한 입력이 들어왔을 때 추출하고자 하는 패턴이 들어오면 1을 출력, 아니면 0을 출력
• Affien function과 Activation function의 합성함수

Affine function

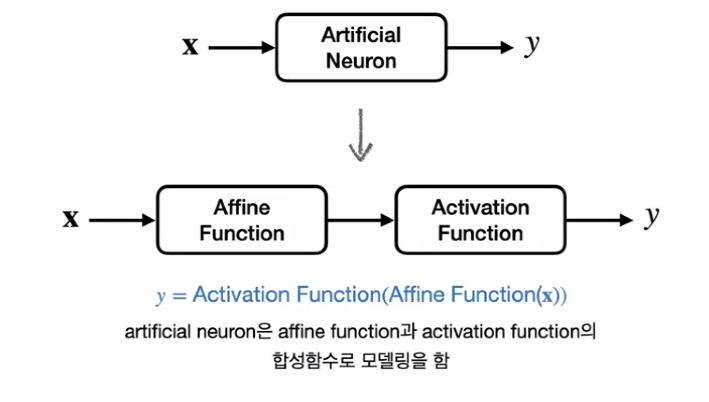
• z : affine value

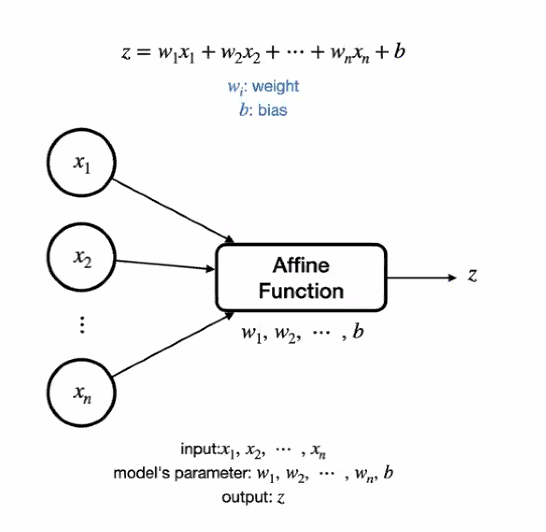
# Affine function 클래스 구현
import numpy as np

class Affine:
  def __init__(self, weight, bias):
    self.weight = weight
    self.bias = bias

  def forward(self, x):
    z = np.sum(self.weight*x) + self.bias
    return z
    
-------------------------------------------
class Affine:
  def __init__(self, weight, bias):
    self.weight = weight
    self.bias = bias

  def __call__(self, x):
    z = np.dot(self.weight,x) + self.bias
    return z
============================================   
w1 = np.array([1,1])
b1 = -1.5

affine1 = Affine(w1,b1)
print(affine1.weight)
print(affine1.bias)

x = np.array([1,1])
affine1.forward(x)

Activaion Function

Sigmoid Function

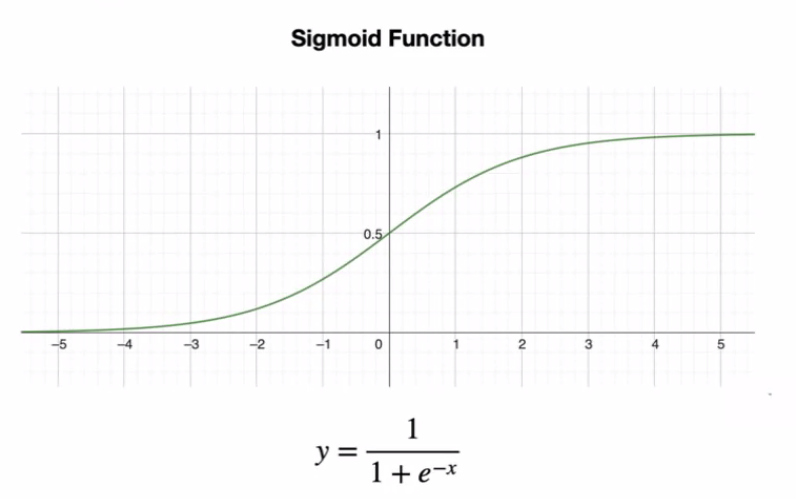
• x에는 affine function 의 affine value값이 들어간다
  
• binary classificaion을 할 때 최종 layer에서 simoid활용

# Sigmoid functoin 클래스 구현
class Sigmoid:
  def __call__(self, z):
    y = 1/(1+np.exp(-z))
    return y
-----------------------------    
class Sigmoid:
  def __init__(self, z):
    self.z = z
  
  def __call__(self):
    y = 1/(1+np.exp(-self.z))
    return y
============================= 
z = affine1.forward(x)
activation = Sigmoid(z)
print(activation()) 

>>
0.6224593312018546

=============================
z= affine2.forward(x)
activation = Sigmoid(z)
print(activation())

>>
0.18242552380635635

# Sigmoid 그래프 그리기
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(20,7))

x = np.arange(-5,5, 0.00001)
z = Sigmoid(x) 

ax.plot(x,z())
ax.hlines(0, -5, 5, color='lightgray')
ax.vlines(0, 0, 1, color='lightgray')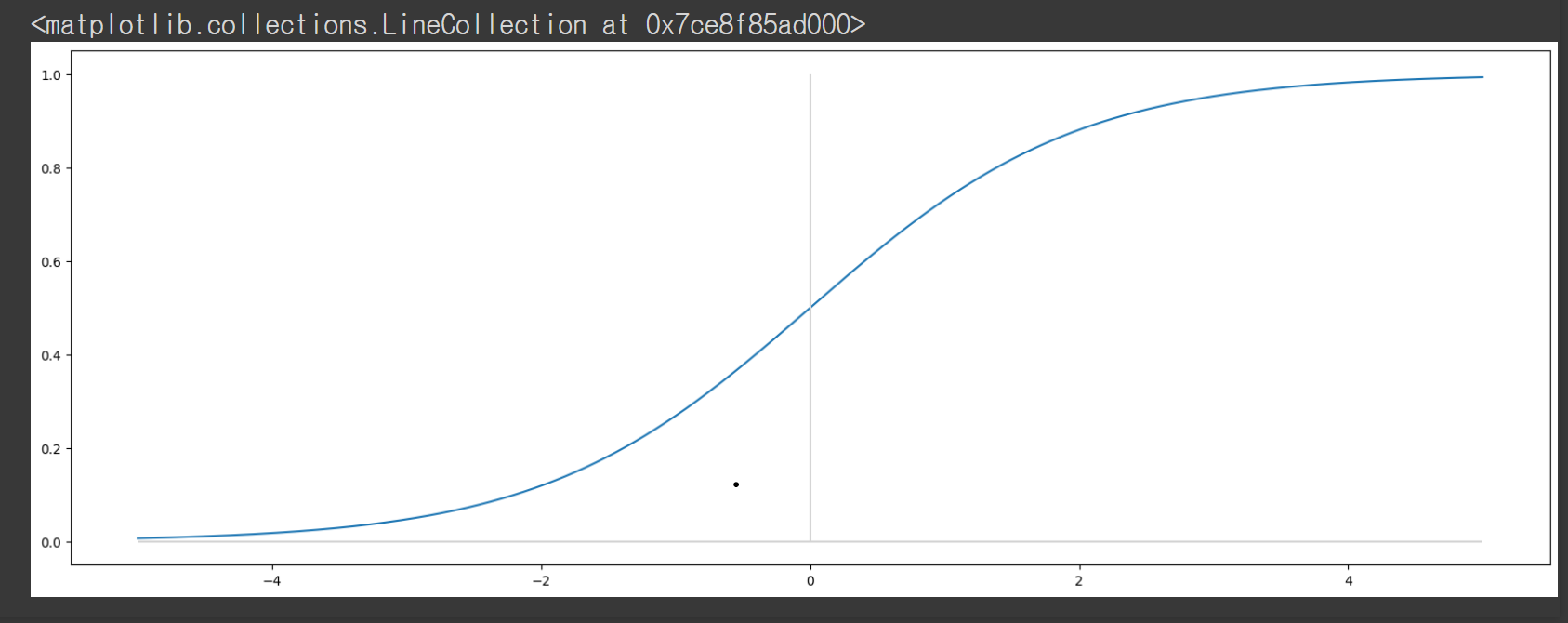

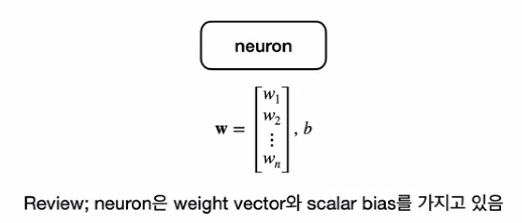
인공뉴런의 재정리

class ArtificialNeuron:
  def __init__(self, weight, bias):
    self.weight = weight
    self.bias = bias
  
  def __call__(self, x):
    object_1 = Affine(self.weight,self.bias)
    object_2 = Sigmoid(object_1(x))
    return object_2()
===============================================
w1 = np.array([1,1])
b1 = -1.5
x = np.array([1,1])

arti_1 = ArtificialNeuron(w1, b1)

arti_1(x)
>>
0.6224593312018546

-----------------------------------------------
## 강사님 정답
class Affine:
  def __init__(self, weight, bias):
    self.weight = weight
    self.bias = bias

  def forward(self, x):
    z = np.dot(self.weight,x) + self.bias
    return z

class Sigmoid:
  def forward(self, z):
    y = 1/(1+np.exp(-z))
    return y   
    
class ArtificialNeuron:
  def __init__(self, weight, bias):
    self.object_1 = Affine(weight, bias)
    self.object_2 = Sigmoid()

  def forward(self, x):
    z = self.object_1.forward(x)
    a = self.object_2.forward(z)
    return a
================================================
w1 = np.array([1,1])
b1 = -1.5
x = np.array([1,1])
arti_2 = ArtificialNeuron(w1, b1)
arti_2.forward(x)

>>
0.6224593312018546

실습

class Model:
  def __init__(self):
    self.AND = ArtificialNeuron(np.array([1,1]), -1.5)
    self.OR= ArtificialNeuron([1,1], -0.5)
    self.NAND = ArtificialNeuron([-1,-1],1.5)

  def forward(self, x):
    a_1 = self.AND.forward(x)
    a_2 = self.OR.forward(x)
    a_3 = self.NAND.forward(x)
    return a_1, a_2, a_3
==============================================
arti_neu = Model()
arti_neu.forward(x)

>>

(0.6224593312018546, 0.8175744761936437, 0.3775406687981454)

• 정답
  

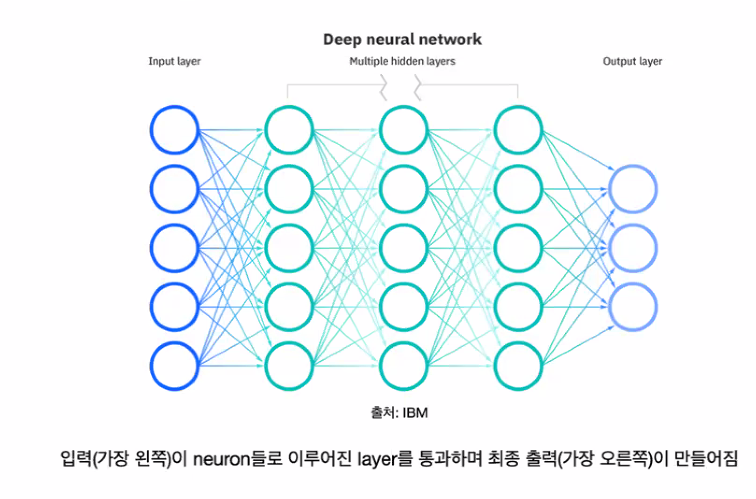
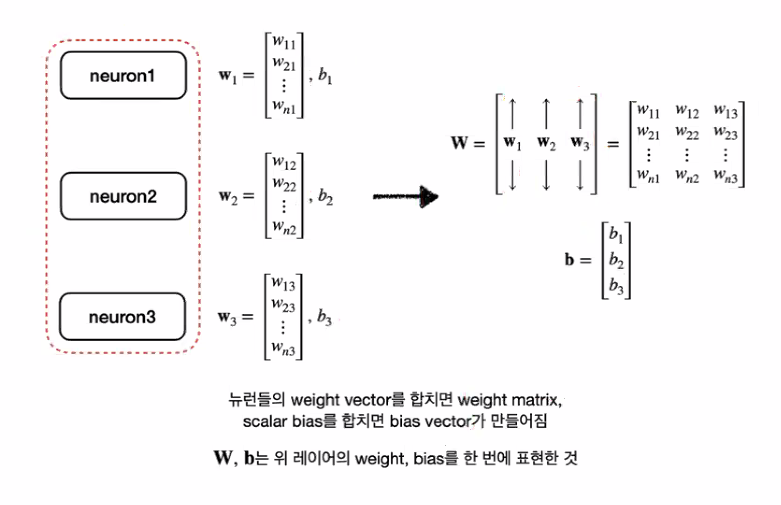
인공 뉴런의 확장

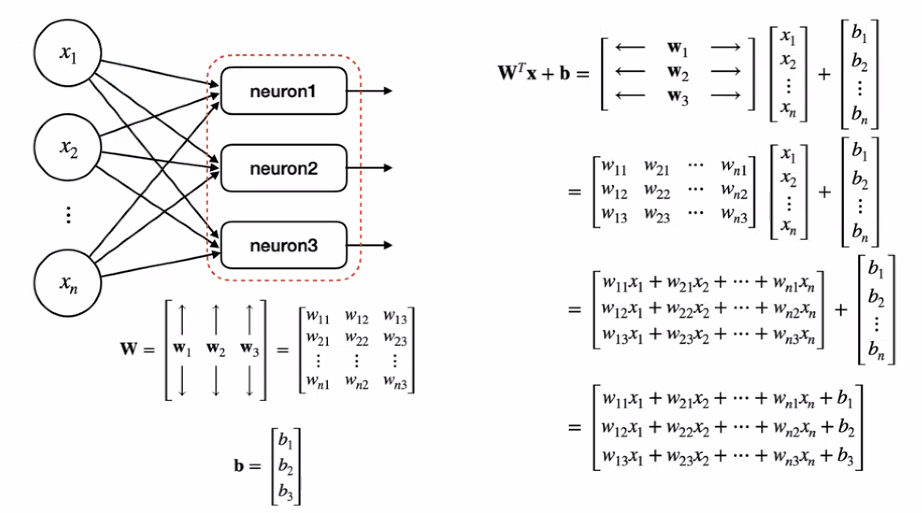
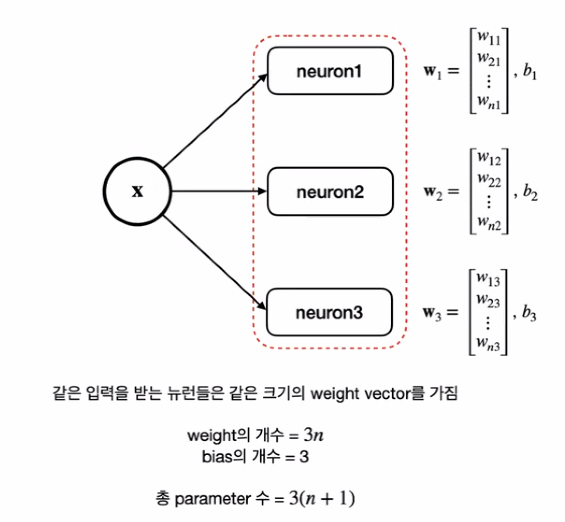
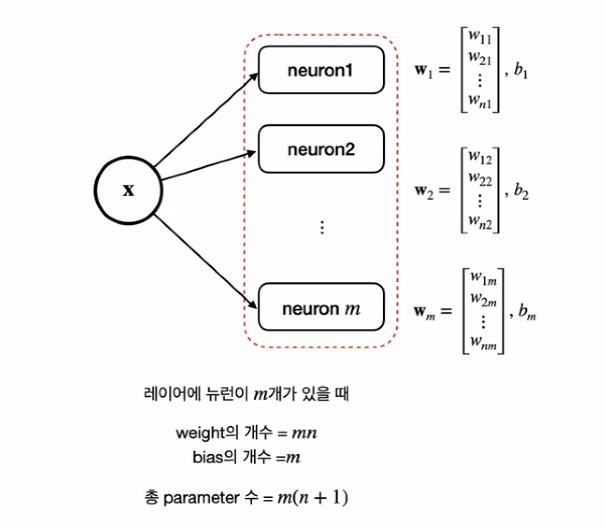
Quiz

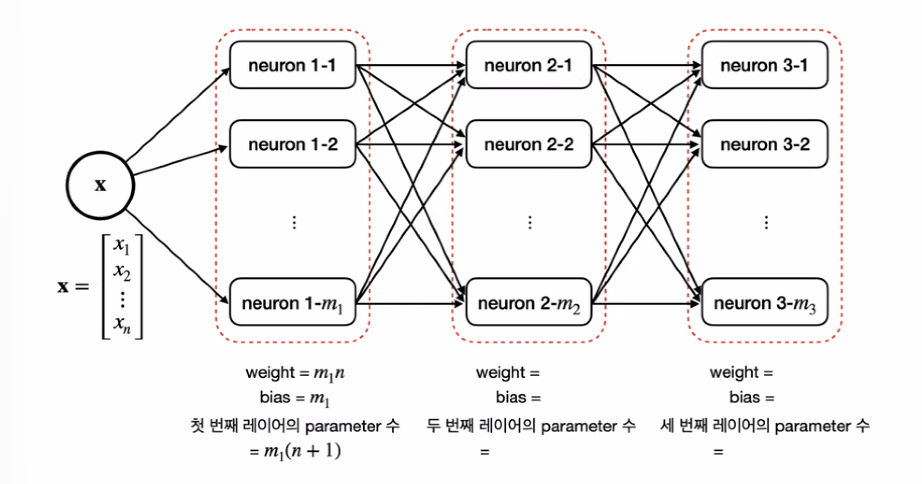
weight = m_2 * m_1
bias = m_2
두번 째 레이어의 파라미터 수 = m_2(m_1+1)

weight = m_3 * m_2
bias = m_3
세번 째 레이어의 파라미터 수 = m_3(m_2+1)

• model complexity(복잡도)는 parameter수 (w, b의 총 수)와 관련된다