<수업 내용>
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
n_samples = 100
X, y = make_blobs(n_samples = n_samples, centers =2, n_features = 2, cluster_std = 0.5)
fig, ax =plt.subplots(figsize = (10,10))
X_pos, X_neg = X[y==1], X[y==0]
print(X.shape)
ax.scatter(X_pos[:,0], X_pos[:,1], color='blue')
ax.scatter(X_neg[:,0], X_neg[:,1], color='red')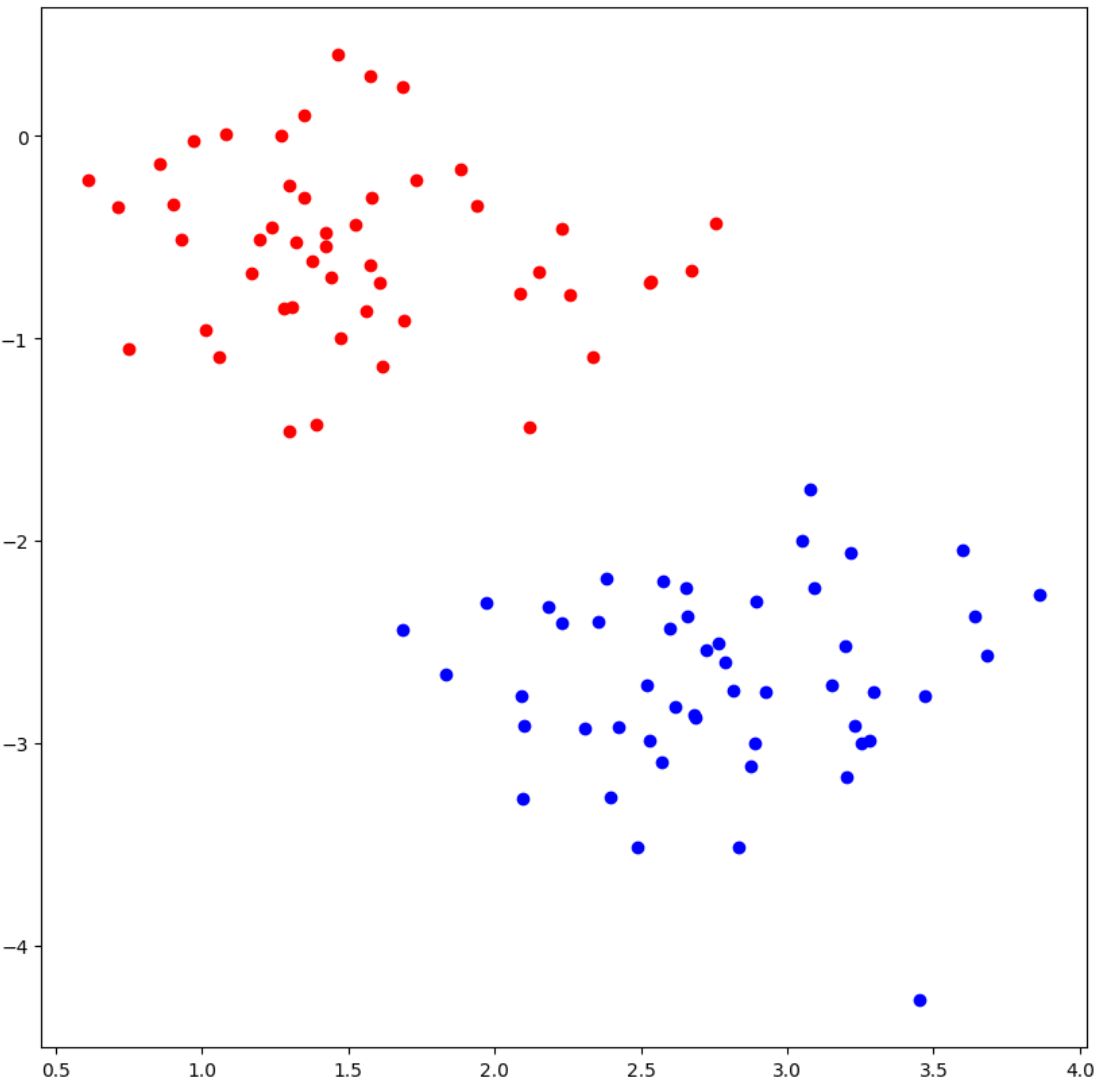
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
n_samples = 300
X, y = make_moons(n_samples = n_samples, noise= 0.2)
fig, ax =plt.subplots(figsize = (10,10))
X_pos, X_neg = X[y==1], X[y==0]
ax.scatter(X_pos[:,0], X_pos[:,1], color='blue')
ax.scatter(X_neg[:,0], X_neg[:,1], color='red')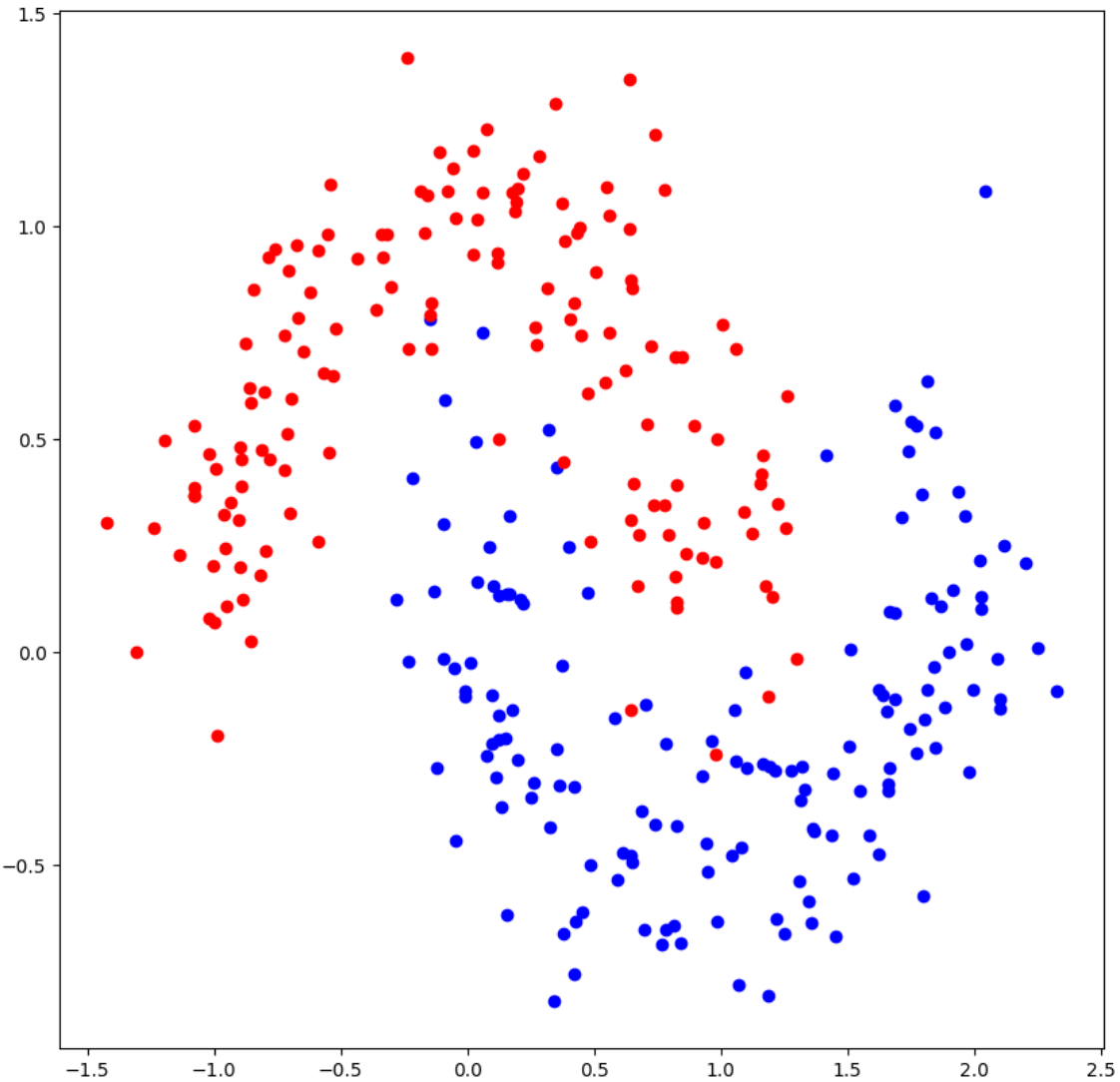
pytorch로 dataset load하기
import torch
from torch.utils.data import TensorDataset, DataLoader
n_samples = 100
X, y = make_blobs(n_samples = n_samples, centers =2, n_features = 2, cluster_std = 0.7)
#torch.FloatTensor(X) : floattensor를 만드는 class
dataset = TensorDataset(torch.FloatTensor(X), torch.FloatTensor(y))
for X_, y_ in dataset:
print(type(X_), X_.shape, X_.dtype)
print(type(y_), y_.shape, y_.dtype)
print(X_)
print(y_)
break
>>
<class 'torch.Tensor'> torch.Size([2]) torch.float32
<class 'torch.Tensor'> torch.Size([]) torch.float32
tensor([1.8940, 6.9193])
tensor(1.) import torch
from torch.utils.data import TensorDataset, DataLoader
n_samples = 100
X, y = make_blobs(n_samples = n_samples, centers =2, n_features = 2, cluster_std = 0.7)
#torch.FloatTensor(X) : floattensor를 만드는 class
dataset = TensorDataset(torch.FloatTensor(X), torch.FloatTensor(y))
BATCH_SIZE = 8 #data를 한번에 load 할 양
dataloader = DataLoader(dataset, batch_size = BATCH_SIZE) #dataloader : batchsize만큼 data를 한번에 load해 주는 메서드
for X_, y_ in dataloader:
print(type(X_), X_.shape, X_.dtype)
print(type(y_), y_.shape, y_.dtype)
print(X_)
print(y_)
break
>>
<class 'torch.Tensor'> torch.Size([8, 2]) torch.float32
<class 'torch.Tensor'> torch.Size([8]) torch.float32
tensor([[ 4.7921, 3.5826],
[ 8.7273, -0.9124],
[ 9.0776, -1.3126],
[ 4.2654, 4.9099],
[ 8.8519, -0.5153],
[ 8.5880, -1.4699],
[ 4.0224, 4.3872],
[ 3.7717, 3.1926]])
tensor([1., 0., 0., 1., 0., 0., 1., 1.])Linear Function

- 한 개 layer의 affine함수를 만들어준다

- weight는 들어오는 data의 feature의 수에 영향을 받는다
- 위의 코드는 뉴런 하나의 weight의 개수는 8개, bias는 1개
- 위의 코드는 layer의 뉴런이 4개 이다.(out_fearures = 4이므로)
- layer의 parameter수는 36개 (weight : 4*8개 , bias :4개)
import torch.nn as nn
fc = nn.Linear(in_features= 8, out_features = 4)
print(fc.weight.shape)
print(fc.bias.shape)
>>
torch.Size([4, 8])
torch.Size([4])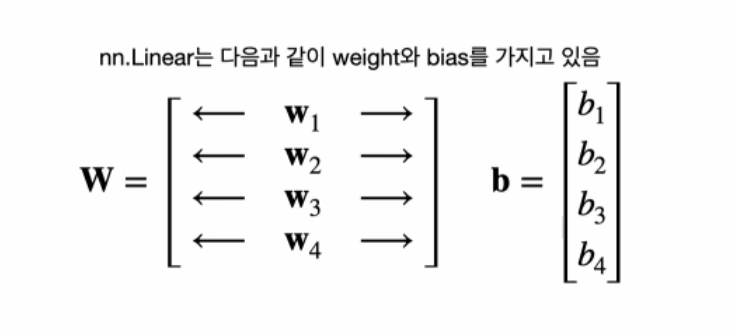
import torch.nn as nn
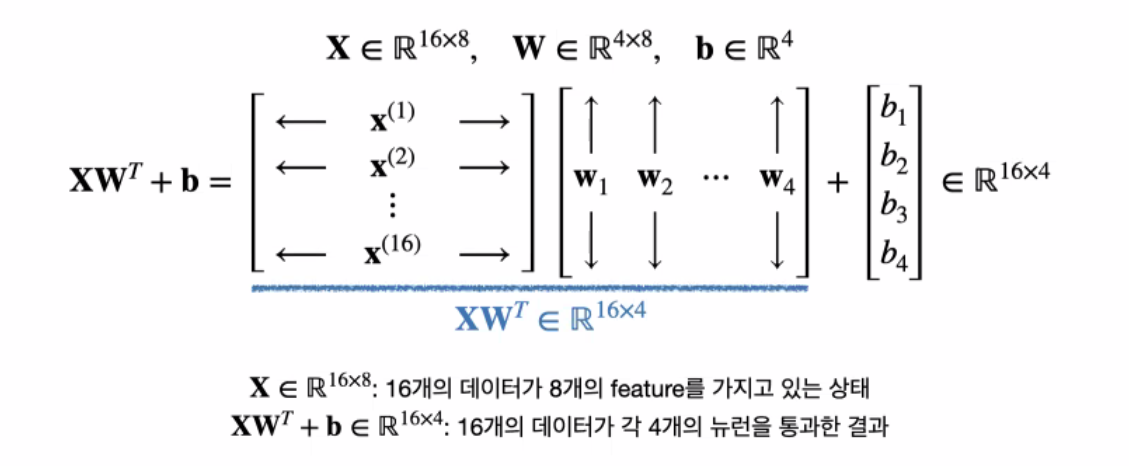
test_input = torch.randn(size=(16,8))
fc = nn.Linear(in_features= 8, out_features = 4)
test_out = fc(test_input)
print(test_input.shape)
print(test_out.shape)
>>
torch.Size([16, 8])
torch.Size([16, 4])
Sigmoid Function
test_input = torch.randn(size =(2,3))
sigmoid = nn.Sigmoid()
test_output = sigmoid(test_input)
print(test_input)
print(test_output)
print(1/(1+torch.exp(-test_input)))
>>
tensor([[-0.8455, 0.9856, 1.4624],
[-0.7175, 0.6302, 0.5391]])
tensor([[0.3004, 0.7282, 0.8119],
[0.3280, 0.6525, 0.6316]])
tensor([[0.3004, 0.7282, 0.8119],
[0.3280, 0.6525, 0.6316]])Loss Function
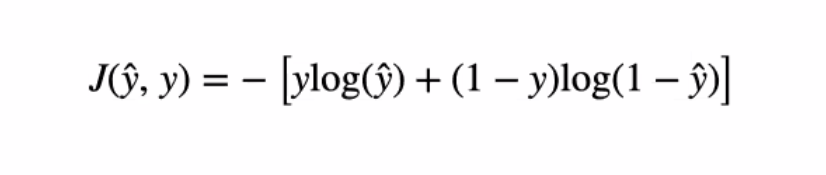
test_pred = torch.tensor([0.8])
test_y = torch.tensor([1.])
loss_function = nn.BCELoss()
test_output = loss_function(test_pred, test_y)
print(test_pred)
print(test_y)
print(test_output)
print(-(test_y*torch.log(test_pred) + (1-test_y)*torch.log(1- test_pred)))
>>
tensor([0.8000])
tensor([1.])
tensor(0.2231)
tensor([0.2231])pytorch model 기본 구조
class Model(nn.Module):
def __init_(self):
super(Model, self).__init__()
def forward(self, x):
pass - 부모 클래스의 메소드를 호출하는 경우는 "super().메소드이름" 형태로 호출
딥러닝 model 만들기
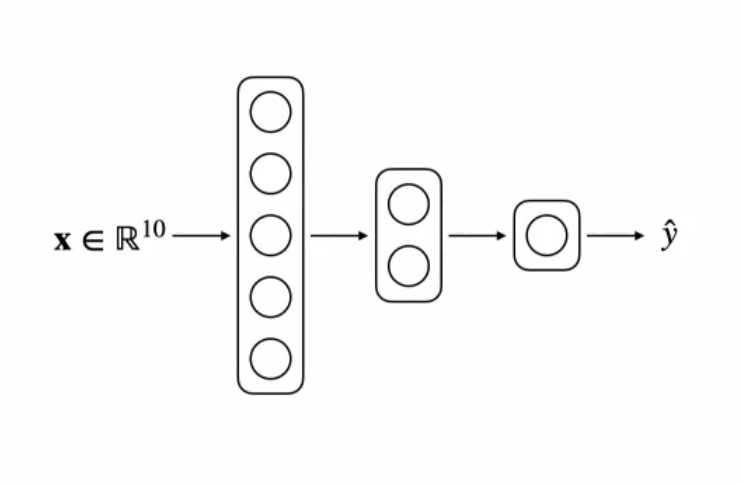
class Model(nn.module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = nn.Linear(in_features= 10, out_features = 5)
self.simoid1 = nn.Sigmoid()
self.linear2 = nn.Linear(in_features= 5, out_features = 2)
self.simoid2 = nn.Sigmoid()
self.linear3 = nn.Linear(in_features= 2, out_features = 1)
self.simoid3 = nn.Sigmoid()
def forward(self, x):
z1 = self.linear1(x)
y1 = self.sigmoid(z1)
z2 = self.linear2(y1)
y2 = self.sigmoid(z2)
z3 = self.linear3(y2)
y3 = self.sigmoid(z3)
return y3

make_blobs 딥러닝 학습 시키기
import numpy as np
N_SAMPLES = 100
X, y = make_blobs(n_samples = n_samples, centers =2, n_features = 2, cluster_std = 0.7)
dataset = TensorDataset(torch.FloatTensor(X), torch.FloatTensor(y))
BATCH_SIZE = 10
dataloader = DataLoader(dataset, batch_size = BATCH_SIZE)
class SimpleModel(nn.Module):
def __init__(self):
super(SimpleModel, self).__init__()
self.linear1 = nn.Linear(in_features= 2, out_features = 1)
self.sigmoid1 = nn.Sigmoid()
def forward(self, x):
z1 = self.linear1(x)
y1 = self.sigmoid1(z1)
x = y1.view(-1) #벡터로 reshape해주는 메서드. (B,1)을 (B,)로 만들어준다
return x
from torch.optim import SGD
LR = 0.1
if torch.cuda.is_available() : DEVICE = 'cuda'
elif torch.backends.mps.is_available() : DEVICE ='mps'
else: DEVICE = 'cpu'
model = SimpleModel().to(DEVICE)
loss_function = nn.BCELoss()
optimizer = SGD(model.parameters(), lr = LR)
# Stochastic Gradient Descent.
EPOCHS = 10
loss_list=[]
acc_list =[]
for epochs in range(EPOCHS):
epoch_loss = 0.
n_corrects = 0
for X, y in dataloader:
X, y = X.to(DEVICE), y.to(DEVICE)
pred = model.forward(X)
loss = loss_function(pred, y)
# loss값은 batch size 데이터의 평균값으로 나온다
# 모델의 weight, bias의 parameters를 업데이트 해주는 부분
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss +=loss.item() *len(X)
# *len(X) : 평균 loss값에 대해 10개의 loss값을 계산한다
#.item() : 텐서를 스칼라로 만들어주는 메서드
pred = (pred > 0.5).type(torch.float)
n_corrects +=(pred ==y).sum().item()
epoch_loss /= N_SAMPLES
loss_list.append(epoch_loss)
epoch_acc = n_corrects/ N_SAMPLES
acc_list.append(epoch_acc)
print(f'Epoch : {epochs +1}')
print(f'Loss : {epoch_loss: .4f}\n')
print(f'Acc: {epoch_acc:.4f}')
fig, ax = plt.subplots(2,1, figsize=(10,5))
ax[0].plot(loss_list)
ax[1].plot(acc_list)
ax[0].tick_params(labelsize=10)
ax[1].tick_params(labelsize=10)
ax[1].set_xlabel("Epoch", fontsize=15)
ax[0].set_ylabel("BCE Loss", fontsize = 15)
ax[1].set_ylabel("Accuracy", fontsize = 15)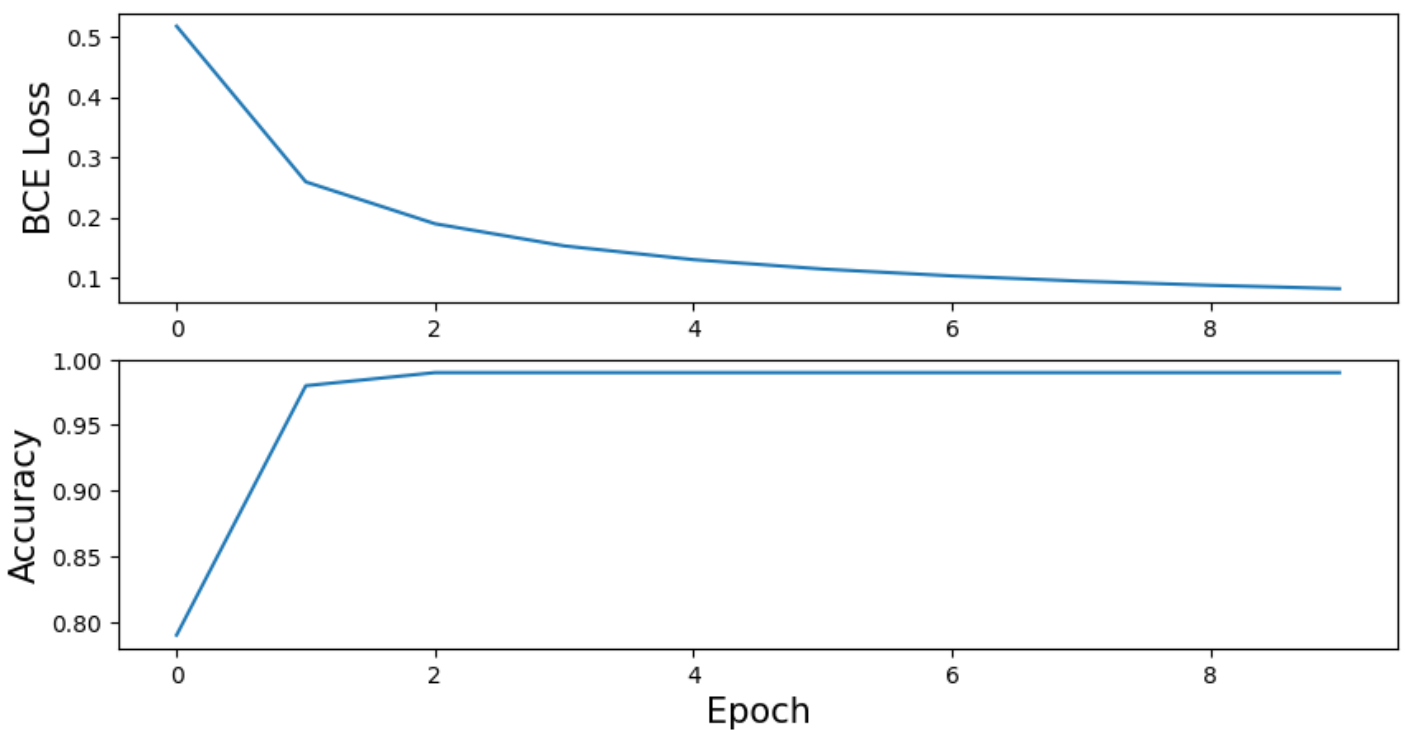
#optimizer.zero_grad(): 모델 내부의 이전 그래디언트(gradient) 값을 초기화합니다. 모델을 학습할 때, 각각의 매개변수는 해당 그래디언트 값을 가지고 있는데, 이 단계에서는 이전에 계산된 그래디언트 값을 초기화하여 새로운 그래디언트 값을 계산할 준비를 합니다.
#loss.backward(): 손실 함수(loss function)를 사용하여 현재 데이터 배치에 대한 손실을 계산합니다. 그 다음, 손실 값에 대한 역전파(backpropagation)가 이루어져 각 매개변수에 대한 손실 함수의 그래디언트를 계산합니다. 이를 통해 모델이 어떻게 업데이트되어야 하는지에 대한 정보를 얻을 수 있습니다.
#optimizer.step(): 옵티마이저(optimizer)를 사용하여 계산된 그래디언트에 따라 모델의 매개변수를 업데이트합니다. 이는 경사하강법(gradient descent)과 같은 최적화 알고리즘을 사용하여 모델의 매개변수를 조정하여 손실을 최소화하려는 것을 의미합니다.
