[Algorithm/자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) - Python

문지은·2023년 5월 7일

algorithm python

Algorithm with Python

목록 보기

5/19

⭐️ 우선순위 큐(Priority Queue)

우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조
우선순위 큐는 데이터를 우선순위에 따라 처리하고 싶을 때 사용

자료구조 추출되는 데이터
스택(Stack) 가장 나중에 삽입된 데이터
큐(Queue) 가장 먼저 삽입된 데이터
우선순위 큐(Priority Queue) 가장 우선순위가 높은 데이터

자료구조	추출되는 데이터
스택(Stack)	가장 나중에 삽입된 데이터
큐(Queue)	가장 먼저 삽입된 데이터
우선순위 큐(Priority Queue)	가장 우선순위가 높은 데이터

우선순위 큐를 구현하는 방법

리스트를 이용하여 구현하기
힙(heap)을 이용하여 구현하기

우리는 힙(heap)을 이용하여 구현하는 방법에 대해 알아볼 것 !
- 단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일하다. (힙 정렬)
데이터의 개수가 N개일 때, 구현 방식에 따른 시간 복잡도

우선순위 큐 구현 방식 삽입 시간 삭제 시간
리스트 O(1) O(N)
힙(Heap) O(logN) O(logN)

우선순위 큐 구현 방식	삽입 시간	삭제 시간
리스트	O(1)	O(N)
힙(Heap)	O(logN)	O(logN)

⭐️ 힙(Heap)

힙은 완전 이진 트리 자료구조의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
- 완전 이진 트리 (Complete Binary Tree) 란? 루트(root) 노드부터 시작하여 왼쪽 자식 노드, 오른쪽 자식 노드 순서대로 데이터가 차례대로 삽입되는 트리(tree)
힙에서는 항상 루트 노드(root node)를 제거한다.
힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값 허용하지 않음)

최소 힙(min heap)

루트 노드가 가장 작은 값을 가진다.
따라서 값이 작은 데이터가 우선적으로 제거된다.

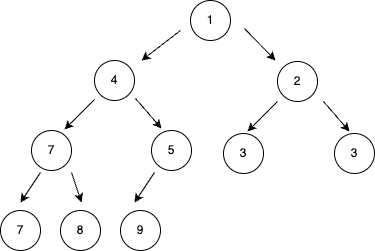
최대 힙(max heap)

루트 노드가 가장 큰 값을 가진다.
따라서 값이 큰 데이터가 우선적으로 제거된다.

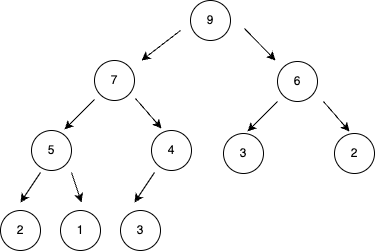
💫 heapq 모듈로 힙 자료구조 사용하기

파이썬의 heapq 모듈은 이진 트리(binary tree) 기반의 최소 힙(min heap) 자료구조를 제공

모듈 임포트

heapq 모듈은 내장 모듈이기 때문에 파이썬만 설치되어 있으면 다음과 같이 간단하게 임포트 후에 힙 관련 함수를 사용할 수 있다.

from heapq import heappush, heappop //, ... 다른 함수들

최소 힙 생성

heapq 모듈에은 파이썬의 보통 리스트를 마치 최소 힙처럼 다룰 수 있도록 도와준다.
Java의 PriorityQueue 클래스처럼 리스트와 별개의 자료구조가 아니므로 일단 빈 리스트를 생성해놓은 다음, heapq 모듈의 함수를 호출할 때 마다 이 리스트를 인자로 넘겨야 한다.
- 즉, 파이썬에서는 heap 모듈을 통해 원소를 추가하거나 삭제한 리스트가 최소 힙이다.

heap = []

힙에 원소 추가하기

heapq 모듈의 heappush() 함수를 이용하여 힙에 원소를 추가할 수 있다.
첫번째 인자는 원소를 추가할 대상 리스트이며 두번째 인자는 추가할 원소를 넘긴다.
내부적으로 이진 트리에 원소를 추가하는 heappush() 함수는 O(log(n))의 시간 복잡도를 가진다.

from heapq import heappush

heappush(heap, 4)
heappush(heap, 1)
heappush(heap, 7)
heappush(heap, 3)
print(heap)  # [1, 3, 7, 4]

힙에서 원소 삭제하기

heapq 모듈의 heappop() 함수를 이용하여 힙에서 원소를 삭제할 수 있다.
원소를 삭제할 대상 리스트를 인자로 넘기면, 가장 작은 원소를 삭제 후에 그 값을 리턴한다.
내부적으로 이진 트리로 부터 원소를 삭제하는 heappop() 함수도 역시 O(log(n))의 시간 복잡도를 가진다.

from heapq import heappop

print(heappop(heap))  # 1
print(heap)  # [3, 4, 7]

최소값 삭제하지 않고 얻기

힙에서 최소값을 삭제하지 않고 단순히 읽기만 하려면 일반적으로 리스트의 첫번째 원소에 접근하듯이 인덱스를 통해 접근하면 된다.

print(heap[0])  # 3

여기서 주의사항은 인덱스 0에 가장 작은 원소가 있다고 해서, 인덱스 1에 두번째 작은 원소, 인덱스 2에 세번째 작은 원소가 있다는 보장은 없다는 것이다.
- 힙은 heappop() 함수를 호출하여 원소를 삭제할 때마다 이진 트리의 재배치를 통해 매번 새로운 최소값을 인덱스 0에 위치시키기 때문이다.
따라서 두번째로 작은 원소를 얻으려면 바로 heap[1]으로 접근하면 안 되고, 반드시 heappop()을 통해 가장 작은 원소를 삭제 후에 heap[0]를 통해 새로운 최소값에 접근해야 한다.

기존 리스트를 힙으로 변환하기

이미 원소가 들어있는 리스트 힙으로 만들려면 heapq 모듈의 heapify()라는 함수에 사용하면 된다.

from heapq import heapify

heap = [4, 1, 7, 3, 8, 5]
heapify(heap)
print(heap)  # [1, 3, 5, 4, 8, 7]

heapify() 함수에 리스트를 인자로 넘기면 리스트 내부의 원소들의 위에서 다룬 힙 구조에 맞게 재배치되며 최소값이 0번째 인덱스에 위치된다.
- 즉, 비어있는 리스트를 생성한 후 heappush() 함수로 원소를 하나씩 추가한 효과와 같다.
- 따라서 heapify() 함수의 성능은 인자로 넘기는 리스트의 원소수에 비례하므로 O(n)의 시간 복잡도를 가진다.
heapify() 함수를 사용할 때 주의할 점은 새로운 리스트를 반환하는 것이 아니라 인자로 넘긴 리스트에 직접 변경한다는 것이다.
- 따라서 원본 리스트의 형태를 보존해야되는 경우에는 반드시 해당 리스트를 복제한 후에 인자로 넘겨야 한다.

nums = [4, 1, 7, 3, 8, 5]

heap = nums[:]
heapify(heap)

print(nums)  # [4, 1, 7, 3, 8, 5]
print(heap)  # [1, 3, 5, 4, 8, 7]

최대 힙

heapq 모듈은 최소 힙(min heap)을 기능만을 동작하기 때문에 최대 힙(max heap)으로 활용하려면 약간의 요령이 필요하다.
- 힙에 튜플(tuple)를 원소로 추가하거나 삭제하면, 튜플 내에서 맨 앞에 있는 값을 기준으로 최소 힙이 구성되는 원리를 이용하는 것이다.
따라서, 최대 힙을 만들려면 각 값에 대한 우선 순위를 구한 후, (우선 순위, 값) 구조의 튜플(tuple)을 힙에 추가하거나 삭제한다.
- 그리고 힙에서 값을 읽어올 때는 각 튜플에서 인덱스 1에 있는 값을 가져온다.

from heapq import heappush, heappop

nums = [4, 1, 7, 3, 8, 5]
heap = []

for num in nums:
  heappush(heap, (-num, num))  # (우선 순위, 값)

while heap:
  print(heappop(heap)[1])  # index 1

n번째 최소값 / 최대값

최소 힙이나 최대 힙을 사용하면 n 번째로 작은 값이나 n 번째로 큰 값을 효과적으로 구할 수 있다.
n 번째 최소값을 구하기 위해서는 주어진 배열로 힙을 만든 후, heappop() 함수를 n 번 호출하면 된다.

from heapq import heappush, heappop

def nth_smallest(nums, n):
    heap = []
    for num in nums:
        heappush(heap, num)

    nth_min = None
    for _ in range(n):
        nth_min = heappop(heap)

    return nth_min

print(nth_smallest([4, 1, 7, 3, 8, 5], 3))  # 4

heapify() 함수를 활용하면 힙을 만들 때 굳이 루프를 돌면서 숫자를 매번 하나씩 추가해 줄 필요가 없다.

from heapq import heapify, heappop

def nth_smallest(nums, n):
    heapify(nums)

    nth_min = None
    for _ in range(n):
        nth_min = heappop(nums)

    return nth_min

heapq 모듈에 이미 이러한 용도로 사용할 수 있는 nsmallest()라는 함수가 존재한다.
- nsmallest() 함수는 주어진 리스트에서 가장 작은 n개의 값을 담은 리스트를 반환한다.
- 그 결과 리스트의 마지막 값이 n 번째 작은 값이다.

from heapq import nsmallest

nsmallest(3, [4, 1, 7, 3, 8, 5])[-1]

반대로 n 번째 최대값을 구할 때는 nlargest() 함수를 사용하면 된다.

from heapq import nlargest

nlargest(3, [4, 1, 7, 3, 8, 5])[-1]

🔥 힙 정렬

힙 정렬(heap sort)은 위에서 알아본 힙 자료구조의 성질을 이용한 대표적인 정렬 알고리즘이다.
다음은 최소 힙(min heap)을 이용하여 배열을 오름차순 정렬하는 코드를 작성한 것이다.

from heapq import heappush, heappop

def heap_sort(nums):
  heap = []
  # 모든 원소를 차례대로 힙에 삽입
  for num in nums:
    heappush(heap, num)
	
  sorted_nums = []
  # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
  while heap:
    sorted_nums.append(heappop(heap))
  return sorted_nums

print(heap_sort([4, 1, 7, 3, 8, 5]))  # [1, 3, 4, 5, 7, 8]

내림차순 힙 정렬을 구현하기 위해서는 최대 힙을 사용하여야 한다.

from heapq import heappush, heappop

def heapsort(nums):
    heap = []
    # 모든 원소를 차례대로 힙에 삽입
    for num in nums:
        heappush(heap, (-num, num))

    result = []
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    while heap:
        result.append(heappop(heap)[1])
    return result

print(heapsort([4, 1, 7, 3, 8, 5]))  # [8, 7, 5, 4, 3, 1]

💫 파이썬의 heapq 모듈 구현하기

위에서 알아본 heapq 모듈을 파이썬 코드로 직접 구현해보면서, heap 자료구조에 대해 더 자세히 알아보자.

heappush 구현하기

그림으로 이해하기

[3, 4, 6, 8, 5, 7]라는 힙에 원소 2를 추가한다고 해보자.

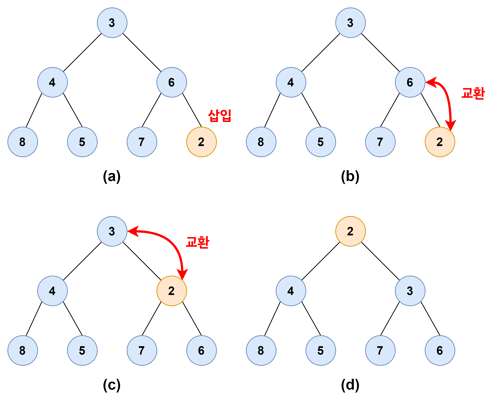
(a) : 가장 끝에 2를 넣는다.
(b) : 2가 부모인 6보다 작으므로 서로 자리를 바꾼다.
(c) : 위로 올라간 2가 부모인 3보다 작으므로, 또 자리를 바꾼다.
(d) : 힙의 성질을 만족했으므로, 끝낸다.

코드 작성하기

배열(리스트) 끝에 새 값을 추가한다.
추가한 원소의 인덱스를 구한다.
부모 인덱스를 구하여 값을 비교한다.
새 값이 부모의 값보다 작으면 값을 교환한다.
- 인덱스를 갱신한다. (자리를 바꿨으므로, 새로 추가한 값의 인덱스가 변했다.)
- 3번으로 돌아가서 같은 과정을 반복하되, 루트에 도달하면 종료한다.
새 값이 부모의 값보다 크거나 같으면 종료한다.

def heappush(heap, data):
    heap.append(data)
    # 추가한 원소의 인덱스를 구한다.
    current = len(heap) - 1
    # 현재 원소가 루트(인덱스 0)에 도달하면 종료
    while current > 0:
        # 추가한 원소의 부모 인덱스를 구한다.
        parent = (current - 1) // 2
        # 새 값이 부모의 값보다 작으면 값을 교환
        if heap[parent] > heap[current]:
            heap[parent], heap[current] = heap[current], heap[parent]
            # 추가한 원소의 인덱스를 갱신한다.
            current = parent
        else:
            break

바로 위 함수에서 부등호의 방향만 바꾸면 최대 힙(max heap)으로 바꿀 수 있다.

def heappush(heap, data):
    heap.append(data)
    current = len(heap) - 1
    while current > 0:
        parent = (current - 1) // 2
        # 새 값이 부모의 값보다 크면 교환
        if heap[parent] < heap[current]:
            heap[parent], heap[current] = heap[current], heap[parent]
            current = parent
        else:
            break

heappop 구현하기

그림으로 이해하기

[3, 4, 6, 8, 5, 7] 라는 힙에서 원소 3을 삭제한다고 해보자.

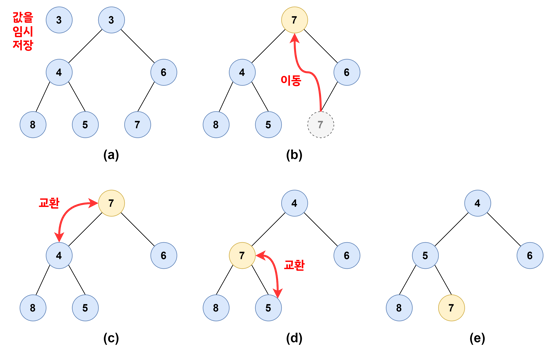
(a) : 루트 노드의 값 3을 임시 저장한다.
(b) : 마지막 노드인 7을 루트로 옮긴다.
(c) : 루트 노드 7을 자식 노드인 4와 6 중에서 작은 값인 4와 자리를 바꾼다.
(d) : 다시 7을 자식 노드인 8과 5 중에서 작은 값인 5와 자리를 바꾼다.

코드 작성하기

heap이 비었으면 "Empty Heap!"을 반환하고 종료
루트 노드만 있으면. pop한 값을 반환하고 종료
루트 노드의 값을 임시 저장한다.
루트 노드에 heap에서 pop한 마지막 값을 넣는다.
현재 노드의 인덱스와 왼쪽 자식 노드의 인덱스를 구한다.
자식 노드의 인덱스가 heap의 길이보다 작으면 반복한다.
- 오른쪽 노드의 인덱스를 구한다.
- 현재의 노드의 값을 왼쪽과 오른쪽 자식의 값과 비교한다.
  ( 더 작은 자식 노드와 비교하기 위해서 )
- 현재 노드의 값이 자식 노드의 값보다 크면 더 작은 자식 노드와 서로 교환한다.
  - 현재 노드의 인덱스를 갱신하고, 왼쪽 자식 노드의 인덱스를 구한다.
- 현재 노드의 값이 자식 노드보다 작으면 반복문을 벗어난다.

def heappop(heap):
    if not heap:
        return "Empty Heap!"
    elif len(heap) == 1:
        return heap.pop()

    pop_data, heap[0] = heap[0], heap.pop()
    current, child = 0, 1
    while child < len(heap):
        sibling = child + 1
        if sibling < len(heap) and heap[child] > heap[sibling]:
            child = sibling
        if heap[current] > heap[child]:
            heap[current], heap[child] = heap[child], heap[current]
            current = child
            child = current * 2 + 1
        else:
            break
    return pop_data

바로 위 함수에서 부등호의 방향만 바꾸면 최대 힙(max heap)으로 바꿀 수 있다.

def heappop(heap):
    if not heap:
        return 0
    elif len(heap) == 1:
        return "Empty Heap!"

    pop_data, heap[0] = heap[0], heap.pop()
    current, child = 0, 1 
    while child < len(heap):
        sibling = child + 1
        # 오른쪽 자식 노드가 왼쪽 자식 노드보다 크면 child = 오른쪽 자식 노드
        # (더 큰 자식 노드와 현재 노드를 비교하기 위해)
        if sibling < len(heap) and heap[child] < heap[sibling]:
            child = sibling
        # 현재 노드와 자식 노드 비교
        # 현재 노드보다 자식 노드가 더 크면 swap하고 현재 노드 인덱스 갱신
        if heap[current] < heap[child]:
            heap[current], heap[child] = heap[child], heap[current]
            current = child
            child = current * 2 + 1
        else:
            break
    return pop_data

heapify 구현하기

[6, 2, 5, 1, 3, 4] 배열을 heapify 한다고 가정해보자.

그림으로 이해하기

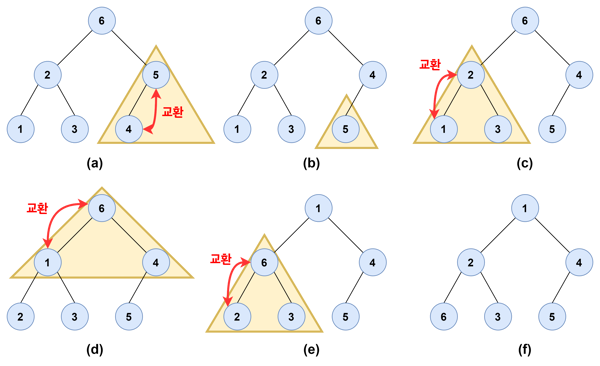
(a) : 가장 마지막 서브 트리를 보면, 왼쪽 자식(4)이 부모(5)보다 작으므로 자리를 교환한다.
(b) : 그럼 아래로 내려간 노드로 인해 힙 구조가 깨질 수 있으므로, 아래로 내려간 노드를 부모 노드로 하는 서브 트리를 살펴본다. 이 경우는 5가 리프 노드이므로 더 살펴볼 필요없다.
(c) : 다음 서브 트리를 본다. 왼쪽과 오른쪽 노드 중 왼쪽 노드의 값이 더 작고, 부모 노드보다 작으므로 자리를 교환한다.
- 아래로 내려간 2는 리프 노드이므로 더 살펴볼 필요없다.
(d) : 다음 서브 트리를 본다. 역시 같은 과정을 거쳐 자리를 교환한다.
(e) : 아래로 내려온 6을 부모로 하는 서브 트리를 힙 구조로 만든다.

코드 작성하기

def heapify(arr):
    last = len(arr) // 2 - 1
    for current in range(last, -1, -1):
        while current <= last:
            child = current * 2 + 1
            sibling = child + 1
            if sibling < len(arr) and arr[child] > arr[sibling]:
                child = sibling
            if arr[current] > arr[child]:
                arr[current], arr[child] = arr[child], arr[current]
                current = child
            else:
                break

바로 위의 함수에서 부등호의 방향만 바꾸면 최대 힙(max heap)으로 바꿀 수 있다.

def max_heapify(arr):
    last = len(arr) // 2 - 1
    for current in range(last, -1, -1):
        while current <= last:
            child = current * 2 + 1
            sibling = child + 1
            if sibling < len(arr) and arr[child] < arr[sibling]:
                child = sibling
            if arr[current] < arr[child]:
                arr[current], arr[child] = arr[child], arr[current]
                current = child
            else:
                break